This post was published in 2021-06-24. Obviously, expired content is less useful to users if it has already pasted its expiration date.
一门Coursera在线课程,全称:Audio Signal Processing for Music Applications
更新日志:
第一次学习:2020-08
第二次学习:2021-06,本文作为复习笔记
本文的初稿会遗漏很多内容:后续补充的内容如果篇幅较小,则会直接修改本文;如果篇幅较大,则可能会另开一篇post,然后在本文的对应位置标注链接。
更新记录:
2021-06-24 初稿完成,头重脚轻版。从第6章开始额外阅读材料和“可选作业”、“领会意图作业”越来越多,暂时先把框架放着,等待后续填入新的内容。
2021-06-28 本系列课程与常规的EE DSP课程有很大关联。如果后续补充的内容没有在本课程里明确提出(比如这个),那么就用紫色字体做标记。拉普拉斯变换
2021-07-04 补充到第2章
2021-07-10 补充到第3章
2022-07-15 补充了一些harmonic series的内容
Table of Contents
第1章:入门知识
1,主要介绍了几种常见工具,包括python, Audacity, sonic visualiser等,此外还包括一些基础复数知识,对应后续的DFT、FFT等课程。
从后续的编程作业来看,python知识主要应用在:matplotlib,ipython(分步执行代码块),numpy数组的处理。
2,编程课主要和wav file有关,作业:使用sms-tools相关的wav file IO lib读取wav file并进行一些基本处理。容易产生混淆的内容是raw wav file读取以后的16bit/24bit/36bit的处理细节,以及是否对读取后的数据采用-1~1的标准化处理。但从后续(第2~8章内容和作业)来看,只要使用sms-tools自带的处理库(而不是混用其他库)就可以忽略这个问题。
补充:如果使用scipy wavRead,则需要注意(至少在目前,标准的scipy)无法处理24bit/36bit的wav文件。所以此时标准化处理读取结果则容易得多,只需要当成16bit来处理即可:
from scipy.io.wavfile import read as wavRead
(fs, x) = wavRead('obo.wav')
x = x / 32768 # 32768=2^15作业1:读取一段wav file,然后把它输出为python array的形式;
作业2:读取一段wav file,然后找array中的最大最小值;
作业3:python array indexing,对python array进行单纯的取indexing value处理;
作业4:Desampling Audio,改变音频的sampling rate。在这里首次提到了analog signal转变为discrete digital signal,然后提到了最常见的44100Hz。但毕竟是第一周的作业,不太可能要求用其他算法进行desampling audio,所以采用了本周作业3(python array indexing)的算法进行处理。
第2章:Sinusoids和DFT
1,介绍了最基础的DFT公式,包括实信号和复指数信号(仅仅是介绍,并不在本系列课程后续中应用,这门课的绝大部分内容都是非周期离散信号的傅里叶变换,离散周期信号的傅里叶级数推导基本用不上)。
2,引入了本系列课程中的一个重要转换公式:
[mathjax-d]\text { magnitude spectrum: } m X=20 \cdot \log _{10}(abs(x))[/mathjax-d]3,Inverse DFT,仅作为数学公式进行介绍(后续作业证明确实不常用)。
4,两节编程课:分别介绍sinusoids和DFT的python实现,近似等同于本周作业。
作业1:用python代码生成一段sinusoid;
作业2:用python代码生成一段复指数信号表示的sinusoid;
作业3:不能使用现成的DFT/FFT function,用python手动实现DFT;
作业4:接作业3,手动实现一个IDFT;
作业5:实现 magnitude spectrum 公式
本周的5个作业是对本周教授公式(DFT相关)的python实现。
第3章:Fourier Properties
1,介绍了傅里叶变换的一些性质:Linearity,Shift,Symmetry和Convolution。其中Symmetry性质在之后的系列课程中经常出现。
2,介绍了傅里叶变换的其他性质及其应用。在后续课程中应用较多的有:Amplitude in decibels (dB),zero-padding,zero-phase windowing,以及最重要的FFT。
3,用sonic visualiser自带的生成器生成了2中periodic signals:sine和sawtooth,然后用软件对它们进行spectrum分析。
4,接第3节,用sonic visualiser对更复杂的音频进行spectrum分析。
5,使用sms-tools对一段音频进行分析:计算并获取magnitude spectrum和phase spectrum,然后使用inverse fourier进行音频信号的复原计算。
6,编程课1:展示了3段不同的程序,分别是:
①直接用FFT处理[mathjax]triang[/mathjax],主要观察phase spectrum
② 对triang进行处理,把它变成一个实偶信号(real and even),FFT的复数部分为0
③把[mathjax]triang[/mathjax]换成音频信号,对上一个程序进行了一些优化,使用math.floor处理index为奇数的情况;同时在进行最后的FFT计算之前,使用了hamming window(smoothing window的一种)进行处理,大致类似于这样:
import numpy as np
(fs, x) = wavread('wav_path')
# smoothing window
x1 = x[5000, 5000 + M] * np.hamming(M)
# 进行FFT Buffer处理(zero-phase windowing)
...
# 使用scipy—fft进行fft计算
...
7,编程课2:继续上一个编程课的内容,但这次直接使用了sms-tools的DFT分析工具—DFTModel进行处理。DFTModel省去了繁琐的zero-phase windowing中的index切割步骤,直接生成最后的magnitude spectrum和phase spectrum(记为DFT-Anal);同时DFTModel还有IFFT功能,记为DFT-Synth。
这个公式在本周的作业里经常用到:[mathjax-d]n^{\text{th}}\text{bin}(\text{Hz})=n*\frac{\text{Sampling frequency}}{\text{FFT Size}}[/mathjax-d]
作业1:Minimize energy spread in DFT of sinusoids
首先在本题的介绍文字里提到了香农采样定理:"All the input arguments to this function (A, f, phi, fs and t) are real numbers such that A, t and fs are positive, and fs > 2*f to avoid aliasing." 。
香农采样定理:[mathjax]F_s\ >\ 2f_{max}[/mathjax]
另附:什么是 aliasing ?
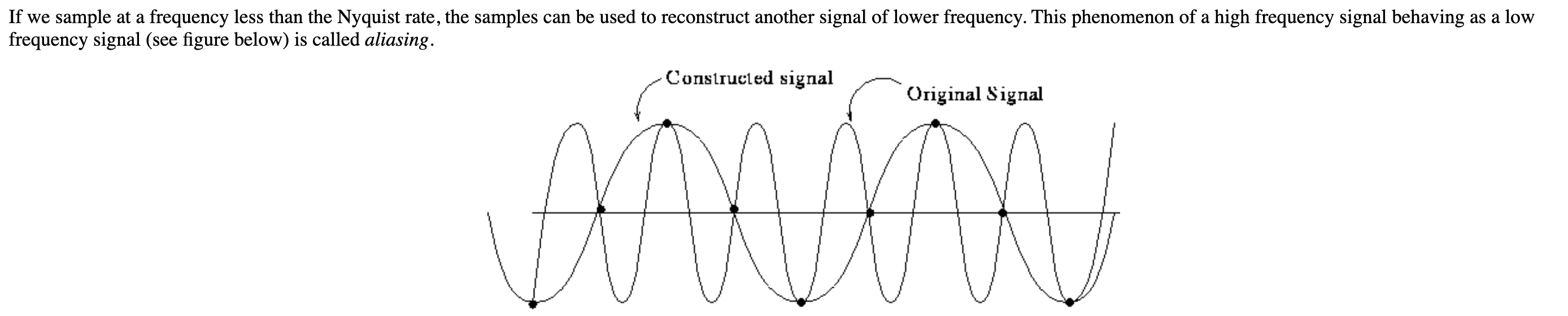
另:务必注意, Nyquist rate ([mathjax]2f_{max}[/mathjax])仍然不满足香农采样定理。
对于没有任何DSP基础的人来说,这道题本身包含了:Frequency bin, energy spread(频谱能量泄漏), [mathjax]f=\frac{1}{T}[/mathjax], DFT magnitude spectrum等知识点的综合应用。虽然题目本身提供了近似送分的最大公约数算法,但题目提供的算法是一个削掉小数部分的化简算法,虽然能通过coursera的test cases,但处理某些信号时会出现严重误差。(详见下面的代码部分)
给定一个input signal,它由2个不同频率的sinusoids叠加而成。为了防止FFT处理后出现严重的energy spread问题,需要在截断信号的时候选取合适的采样点数N,防止“非周期截断”。
[mathjax-d]N=\frac{\frac{F_s}{f1}*\frac{F_s}{f2}}{GCD(\frac{F_s}{f1},\frac{F_s}{f2})}[/mathjax-d]作业2:Optimal zero-padding
在本周的作业1里,我们可以求出简单正弦信号的周期T,所以作业2就是在作业1的基础上再往下做,对截取的信号进行补0(zero padding),然后计算magnitude spectrum. 补0的方法有很多,可以用本系列课程的通用补0方法(zero phase zero padding),也可以直接在时域后面追加0,还可以在时域的头尾加0,等等。这些补0的方法虽然不同,但计算出的频谱图都是完全一样的,所以不论用哪一种补0方法应该都可以通过coursera的自动测验。
例如给定sinusoid,[mathjax]f=250Hz[/mathjax],[mathjax]F_s=10000[/mathjax],有210 samples。那么它的[mathjax]period=\frac{F_s}{f}=40[/mathjax],只需要补充30个采样点,就可以做到[mathjax]\frac{210+30}{40}=6 \in N^+[/mathjax]。当然,尽管最终时域的长度为T的整数倍,但由于补了0,所以magnitude spectrum一定会出现频谱泄漏。
作业3:Symmetry properties of the DFT
Judge if an input signal is real and even. 有很多种方法可以做,但是题目里指定了如下算法进行判断:
首先对input signal进行处理:使用zero-phase windowing处理,但是在此过程中不能出现任何zero-padding。随后进行DFT计算,并对结果进行判断:
如果输入信号是real and even,那么DFT得到结果的复数部分应当全部为0(在实际计算中使用[mathjax]10^{-6}[/mathjax]作为误差标准)
例如:输入信号为[mathjax]\text{np.array}([1, 2, 3, 4, 1, 2, 3])[/mathjax],计算得到的DFT结果为[mathjax-d]\text{np.array}([ 16+0j, 2+0.69j, 2+3.51j, 2-1.08j, 2+1.08j, 2-3.51j, 2-0.69j])[/mathjax-d],那么原输入信号就不满足real and even的条件。
作业4:Suppressing frequency components using DFT model
它真的算滤波器吗?一个最简单的滤波器。对DFT计算的结果进行处理:[mathjax]\leq[/mathjax]70 Hz的频率点一律置为-120dB,然后执行IDFT得到输出信号。
需要用到公式:[mathjax]n^{\text{th}}\text{bin}(\text{Hz})=n*\frac{\text{Sampling frequency}}{\text{FFT Size}}=n*\frac{F_s}{N}[/mathjax]
理想高通滤波器
“最简单的滤波器“其实应该被称为理想高通滤波器(ideal high pass filter):
[mathjax-d]H(j \omega)=\left\lbrace \begin{array}{ll} 0, & |w| \leq \omega_{c} \\ 1, & |w|>\omega_{c} \end{array}\right. [/mathjax-d]相比于处理实际问题的DSP社区,这种滤波器在教科书上出现的更多一些,主要原因还是它存在诸多缺点。它无法处理实时信号(本系列课程要处理的都是已经录制好的音频,并不是无限长的信号/实时信号,这一点倒是不冲突);但即使是处理有限长的信号,也大概率在会在IFFT后出现明显的ringing/smearing缺陷。所以本习题中的处理算法(理想高通滤波器)在现实中几乎不会被使用。
第4章:The Short-Time Fourier Transform (STFT)
为了尽可能降低“非周期截断”带来的频谱泄漏的影响,现在引入各种analysis window,并使用STFT替代上一章使用的DFT/FFT。
1,介绍了各种analysis window,比如rec-window, hann, hamming window, blackman, blackman-harris。由于侧重点不同(或者其他原因),第4章并没有详细讲解各个分析窗带来的旁瓣衰减、频谱混叠等特征影响,也没有非常明确地区别这些分析窗。而从第5章开始,则需要对几个常见窗进行择优选取。
2,介绍了STFT,window-size, fft-size, hop-size以及ISTFT。介绍的STFT参数在后续课程中经常出现,也会在实际应用中反复调整,主要原因还是time-frequency compromise.
3,展示课:用sonic visualizer和sms-tools演示了STFT的计算结果—spectrogram。(从后续的课程来看,99%的内容都围绕magnitude spectrogram,基本上不会涉及到phase spectrogram)
4,展示课:继续用sonic visualizer和sms-tools分析一段真实的音频:如何选取窗口(可惜没有更深入的分析)、如何搭配出效果良好的STFT参数:window-size, fft-size, hop-size。
5,编程课:用python演示各种分析窗。
6,编程课:用sms-tools自带的STFT工具演示STFT。(和DFT相似地,也有STFT_synth和STFT_anal)
作业1:Extracting the main lobe of the spectrum of a window
从现成分析窗的magnitude spectrum里提取main lobe(主瓣)。大约50%的代码是zero-phase windowing等处理,另一半代码用于挨个比较然后找出局部最低值对应的index,然后提取出main lobe。
有的时候在代码里为了让magnitude spectrum看起来更熟悉,可能会用fftshift(),这个时候就要从如下图所示的红叉点开始逐个比较,而不是array[0][0]。
作业2:Measuring noise in the reconstructed signal using the STFT model
Energy of a signal:信号的能量。[mathjax]E=\sum_{n=0}^{N-1}|x[n]|^{2}[/mathjax] . 其中[mathjax]x[n][/mathjax]不能先转换为dB,而应该在信号能量计算完毕后转换:[mathjax]E_{dB}=10\cdot \log_{10}{(E)}[/mathjax] .
[mathjax]E_{noise}[/mathjax]:在本题使用STFT的情形下,[mathjax]E_{noise}[/mathjax]可以认为是原始信号与“经过STFT与I-STFT处理后的输出信号”之间的减法差值。
Signal to noise ratio (SNR) :信噪比。[mathjax]SNR=10\cdot \log_{10}{\frac{E_{signal}}{E_{noise}}}[/mathjax] .
本题仅仅是一道SNR相关的代码实现题,没有涉及到SNR在这个领域内的其他应用。在本系列课程的第5章—第3课,在评估sinusoidal model synthesis的精确程度的时候还会涉及到SNR。
作业3:Computing band-wise energy envelopes of a signal
和作业2类似,计算high energy envelope和low energy envelope。[mathjax]E=\sum_{k=k_1}^{k_2}|x[k]|^{2}[/mathjax] .
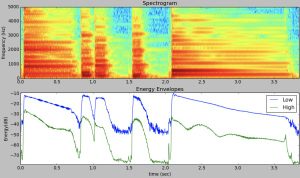
以3000Hz为分界线,0~3000Hz的频率点用于计算low energy envelope,高于3000Hz的频率点用于计算high energy envelope。由于本题(以及本系列课程以后的大多数题)开始使用spectrogram(而不是magnitude spectrum / phase spectrum),所以最终绘图检验结果的x轴并不是frequency (bin),而是time (series)。类似如下图:
第5章:Sinusoidal model
sinusoidal model,正弦波模型,[mathjax]y[n]=\sum_{r=1}^{R} A_r[n]\cos(2\pi f_r [n]n)[/mathjax]
Sinusoidal model可以看作是一种 信息压缩/资料压缩 的方式:一段(自然的)音频,如果用STFT进行分析,会计算出非常、非常多的频率分量,尽管这些频率分量在经过inverse-STFT处理后能较好地还原输入信号,但它们占用的信息量仍然很大,“资料压缩比”很低。现在假设可以使用Sinusoidal model,将这些频率分量进行“精简”,只挑选出极少部分(比如从3000个频率分量里挑选出10个)频率分量用于构建正弦波模型,经过inverse-STFT处理后输出的信号同样也能较好地还原原始输入信号。尽管还原程度略逊于STFT-ISTFT,但大大简化了模型,提高了资料压缩比。
Class 1
介绍sinusoidal model。在执行STFT时,为了让频率分量更容易分辨,需要在analysis window种类的选取、analysis window size的确认上进行一些初步估算:
[mathjax]M\geq B_s\frac{f_s}{|f_{k+1}-f_k|}[/mathjax]其中:[mathjax]M[/mathjax]:分析窗的长度;[mathjax]B_s[/mathjax]:分析窗的主瓣宽度
?本课程中会用到的常见分析窗的主瓣宽度列举如下:
● hanning, hamming : 4 bins
● blackman: 6 bins
● blackman-harris: 8 bins
由此可知,(在确定好了分析窗的种类以后),假如输入信号通过STFT,得到了2个较为接近的正弦分量,那么可能需要考虑再次计算分析窗的长度M,然后重新建立STFT模型进行计算。比如一开始进行估算的时候设置了最低200Hz的正弦频率分量之差([mathjax]|f_{k+1}-f_k|[/mathjax]),但实际计算一遍后在spectrogram里发现了2个正弦信号频率分别为[mathjax](300Hz, 400Hz)[/mathjax],那么就需要重新选取分析窗的长度M,甚至重新选取分析窗的类型。
Class 2
主要内容是从spectrogram的结果里计算出组成sinusoidal model的正弦频率。
在计算spectrogram之前,需要考虑分辨率问题:有zero-padding和spectral interpolation两种算法提高分辨率。在得到spectrogram以后,要从无数频率分量里挑选出用于构建sinusoidal model的正弦频率,就需要peak detection算法。
由于所涉及的都是离散信号,所以很容易通过相邻数值比较的方法找出所有peak (frequency)。但是,peak detection算法仅能计算出STFT单个frame里的peak frequency,要想在整个spectrogram(视为多个STFT magnitude spectrum frames的组合)里确定正弦频率,就需要添加额外判断:
首先假设我们已经确定了一条轨迹线(track)[mathjax]t[/mathjax],这条轨迹线本身已经具备了一定的长度:
[mathjax-d]\exists \ f_t[0], f_t[1], f_t[2]…f_t[L][/mathjax-d]然后我们在下一帧里通过peak detection算出了一个新的peak [mathjax]f_p[/mathjax],现在要考虑是否把这个peak加入track [mathjax]t[/mathjax]中:
如果[mathjax]|f_p-f_t[L]|<threshold[/mathjax]
那么新的peak [mathjax]f_p[/mathjax]也可以加入track [mathjax]t[/mathjax],使得后者的长度+1。
然后开始下一轮计算,直到track的长度无法增加为止。
Class 3
sinusoidal model的合成(synthesis)。
最原始的方法:additive synthesis
[mathjax]y[n]=\sum_{r=1}^{R} A_r[n]\cos(2\pi f_r [n]n)[/mathjax]一个过渡方法,并不会在后续课程中使用
如果要换一种节省计算量的方法:
[mathjax]y[n]=IDFT(A_0mW[k-k_0]e^{j*(pW[k-k0]+\varphi_0)})[/mathjax]其中,[mathjax]mW[k][/mathjax] : analysis window’s magnitude spectrum,[mathjax]pW[k][/mathjax] : analysis window’s phase spectrum.
可以简单描述为:分析窗+单一频率的正弦波=将分析窗的magnitude spectrum和phase spectrum平移到正弦波对应的频率和相位处,所以用这两种spectrum做IDFT,再将所有IDFT的结果叠加,也能做到sinusoidal model的合成。
本课程最后采用了这个算法:
[mathjax]y[n]=IDFT(\sum_{r=0}^{R}A_rmWl[k-k_r]e^{j*(pWl[k-k_r]+\phi_r)})[/mathjax]其中,[mathjax]mWl[k][/mathjax] : analysis window main lobe's magnitude spectrum,[mathjax]pWl[k][/mathjax] : analysis window main lobe's phase spectrum.
如果用整个analysis window进行计算,看起来还是计算量大了一些。这里直接把分析窗的main lobe提取出来进行计算。
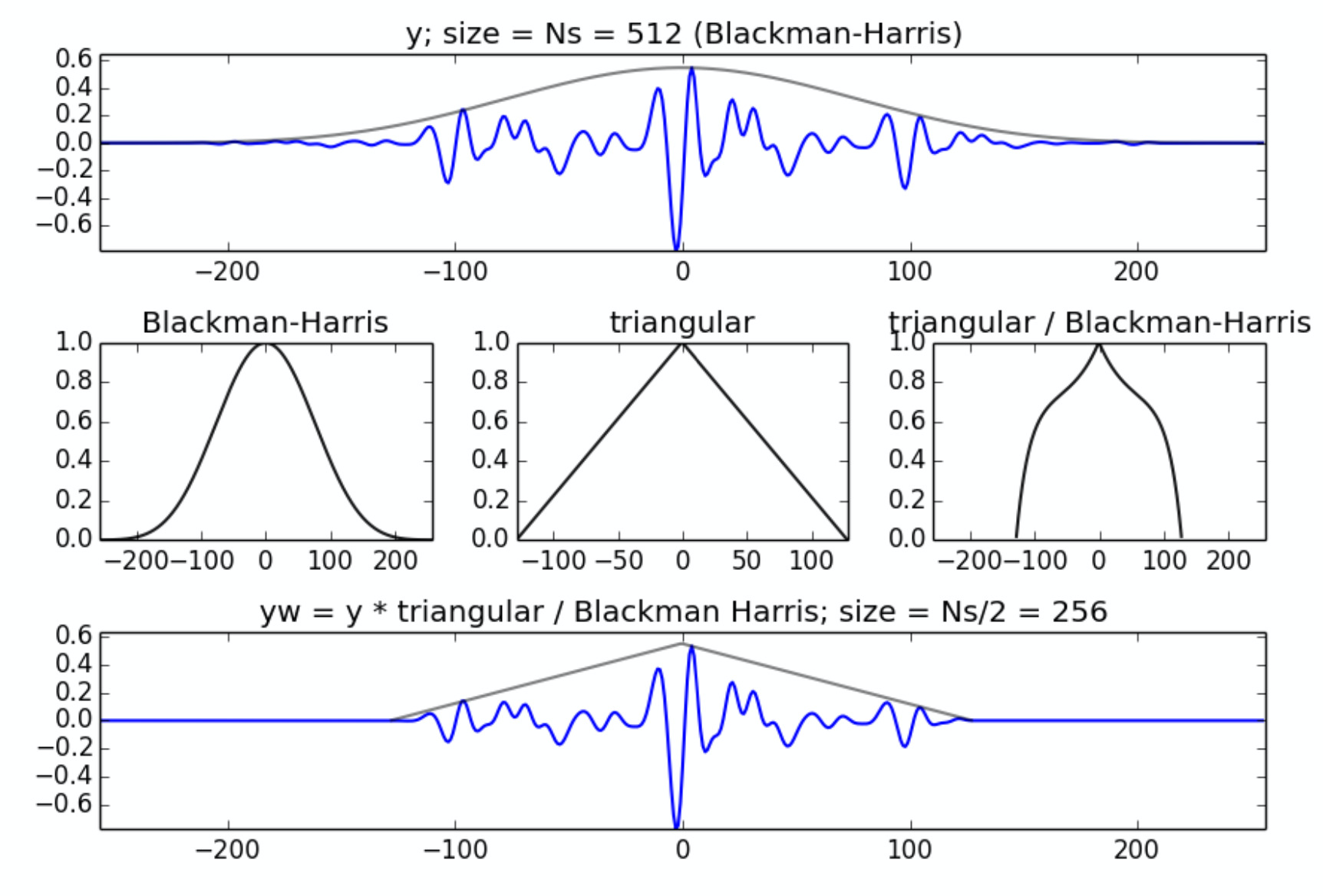
用这个算法做,对analysis window main lobe的宽度有一些要求,见:本课程中会用到的常见分析窗的主瓣宽度列举,所以很多时候主瓣宽度较大的blackman-harris会成为优先选择。但是这样又会带来overlap-add过大的问题,所以本课程在STFT synthesis时使用了一个新的分析窗:[mathjax]yw=y*\frac{triangular}{Blackman Harris}[/mathjax]
编程课
1,主要是sms-tools分析/合成 工具的使用。包括前几章的DFT/ STFT和本章的sinusoidal model。通过分析一些基本音频文件(比如piano.wav, obo.wav),调整分析模型的参数,从而重新回顾前几章的重要内容。
2,从freesound上下载了一个更为复杂的音频,来自现场录制的乐器。在假定并不知道这段音频的频率分布规律的前提下,通过不断试错、调参、更换分析模型,从而最终较为完美地完成了analysis-synthesis .
3,用python实现peak detection相关的内容,此外还有zero-padding和spectral interpolation .
4,搭配上一节课的peak detection代码,用python实现了sinusoidal model synthesis。由于使用的音频时oboSound.wav,所以使用DFT也问题不大。
5,简要解释sms-tools lib里的sinusoidal model - analysis 的代码,并使用这个现成的lib进行演示。
总的来说,从本章开始,较为繁琐的模型实现代码都在sms-tools里,可以直接使用;后续作业更倾向于思维发散、模型选择(尤其是分析窗的选择)、参数选择与调整,以及音频自我创作。
作业
Minimizing the frequency estimation error of a sinusoid
用DFT分析一段音频(事实上是单一频率的正弦波),然后使用sinusoidal model的peak detection估算出输入音频的频率(sms-tools提供了开箱即用的方法)。执行DFT需要window size, fft size,而本题需要求出最佳window size,使得peak detection得出的结果最接近正确答案。本题原则上不允许使用数学公式直接推倒出最佳window size,而是需要写一段brute-force程序,用试错的方法一个一个试出最佳答案。本题的更详细内容可能会另开一篇post写。
Tracking a two component chirp
chirp超出了本系列课程的难度范畴,所以本题不需要自己写代码,只需要修改现有代码的参数,并尝试执行程序,使得输出结果符合要求。本题的更详细内容可能会另开一篇post写。
Tracking sinusoids of different amplitudes
一段输入信号包含了2个正弦频率分量,但是2个正弦波的振幅差异非常非常大。本题超出了本系列课程的难度范畴,所以本题不需要自己写代码,只需要修改现有代码的参数,并尝试执行程序,使得输出结果符合要求。本题的更详细内容可能会另开一篇post写。
Tracking sinusoids using the phase spectrum
完成本题需要的代码非常简单,但题目本身并不容易。需要分析一个包含了“transient”的音频信号,“transient”前后信号的频率是不同的。本题代码包含了一个经过修改的sinusoidal model analysis,以及使用phase spectrum找出"transient"前后的频率分量。本题的更详细内容可能会另开一篇post写。
第6章:Harmonic model
本章两个核心概念的中文翻译:
Fundamental frequency ([mathjax]f_0[/mathjax]):基音频率 / 基频;
Harmonics:泛音
另附一些补充内容:
Harmonic series,泛音列,一般不包括基频[mathjax]f_0[/mathjax](有的时候也称之为overtune);
分音列,一般包括基频[mathjax]f_0[/mathjax]
为什么会存在Harmonic model?可以参考这个wikipedia:🔗 [泛音列 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/泛音列
Harmonics的定义:
When the frequencies of the partials are whole-number multiples of the fundamental frequency, those frequencies are harmonics.
https://pages.uoregon.edu/emi/11.php
Harmonic model, [mathjax]yh[n]=\sum_{r=1}^{R} A_r[n]\cos(2\pi r f_0 [n]n)[/mathjax]
对比sinusoidal model
sinusoidal model, [mathjax]y[n]=\sum_{r=1}^{R} A_r[n]\cos(2\pi f_r [n]n)[/mathjax]
Sinusoidal model本质上还需要记忆并叠加一系列的正弦波,而harmonic model的核心部分仅仅需要记住一个基频,然后通过叠加整数倍正弦波来尽可能接近原有音频信息。
补充:通过Harmonics partial计算出的频率序列和实际上的music note frequency有一定数值差距,这种现象又被称为 inharmonicity ,一般使用 cents 来表示差距的大小:
[mathjax-d]\log _{2}\left(\frac{\omega_{1}}{\omega_{2}}\right) \cdot 1200[/mathjax-d]1,可以看出,从STFT,到sinusoidal model,再到harmonic model,使用的分析模型“资料压缩比”越来越高,模型简化程度越来越高,更有利于对音频信号的分析。(以上内容不能简单地比较优劣)
但并不是所有适用于sinusoidal model的音频信号都适合用harmonic model进行处理,具体还需要初步观察spectrogram的频率分布规律,然后再选择合适的分析模型。
Harmonic model的peak detection算法和sinusoidal model的算法类似:
首先假设我们已经确定了一条轨迹线(track)[mathjax]f_h[/mathjax],这条轨迹线本身已经具备了一定的长度:
[mathjax-d]\exists \ f_h[0], f_h[1], f_h[2]…f_h[L][/mathjax-d]然后我们在下一帧里通过peak detection算出了一个新的peak [mathjax]f_p[/mathjax],现在要考虑是否把这个peak加入track [mathjax]f_h[/mathjax]中:
如果[mathjax]|f_p-h*f_0|<threshold[/mathjax]
那么新的peak [mathjax]f_p[/mathjax]也可以加入track [mathjax]f_h[/mathjax],使得后者的长度+1。
然后开始下一轮计算,直到track的长度无法增加为止。
2,由基本公式可知,harmonic model最核心的部分在于[mathjax]f_0[/mathjax]的获取,所以本节课程主要内容是不同情形下[mathjax]f_0[/mathjax]的算法。但由于这些算法的具体实现超出了本系列课程的范围,所以本节课仅仅列举了这些算法的基本实现。对算法基于的分析数据:有F0 detection in time domain和F0 detection in frequency domain;对算法适用的音频信号:有monophonic signal和polyphonic signal。
Two-way mismatch algorithm也在本节课中一笔带过,但它被sms-tools选为了F0Detection()算法。
3,展示课:使用sms-tools自带的工具(从DFT一直到harmonic model)分析一段基础音频(比如自带的violin.wav),主要讲解关于分析参数的选择与调整。
4,展示课:和上节课的内容部分类似,但这次换成了freesound上下载的一段更复杂的音频进行分析。
5,编程课:F0Detection() . 主要讲解Two-way mismatch algorithm在sms-tools中的代码实现,以及如何在python代码里使用它。
6,编程课:harmonicModelAnal() . 同样由sms-tools封装好了,只需要在代码中直接调用即可。
第7章:Stochastic Model
本章不仅仅是stochastic model,还有其他的一系列(次要)models .
Class 1: Stochastic Model
如果不深入探究stochastic和random的差异,在这节课里可以不严谨地将stochastic model的“stochastic”视为“白噪音”。
[mathjax]yst[n]=\sum_{k=0}^{n-1} u[k]h[n-k][/mathjax]其中,[mathjax]u[n][/mathjax] : white noise ; [mathjax]h[n][/mathjax]:impulse response of filter approximating input signal [mathjax]x[n][/mathjax] .
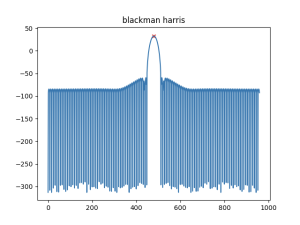
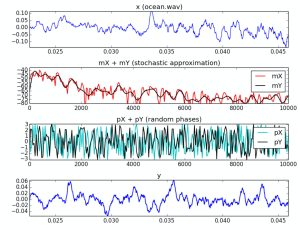
针对一些特定音频信号(比如潮汐声),用常规的STFT处理以后会发现magnitude spectrum拥有的频率分量非常多(见下面一张图),远远超过了前几节课分析的pinao.wav / obo.wav 等音频信号。所以"stochastic"意味着我们需要极大程度“简化”magnitude spectrum的频率分布,然后结合“随机生成的白噪声相位”得到输入音频信号(ISTFT和overlap-add)。由于白噪声每次都是随机生成的,所以我们只需要“记住”简化版的magnitude spectrum即可,大大提高了资料压缩率。
上图中的impulse response of filter approximating input signal(有时也简称approximation或smoothing)有多种相关算法,包括LPC approximation, envelope approximation(在之前的课程中出现过envelope相关的作业)。此外还有一种偷懒的方法:直接调用scipy.signal.resample() . (见本章编程课1)
Class 2 : 其他分析模型
Sinusoidal / harmonic model + residual model (SpR / HpR)
residual model来自于简单的减法:[mathjax]\text{residual component}=x[n]-\text{sinusoidal component}[/mathjax] (harmonic model同理)。
相比于单一的sinusoidal / harmonic model,额外引入的residual component无疑会使得整个模型的资料压缩比降低不少,但并不是所有现实中需要分析的音频信号都可以用sinusoidal / harmonic 这样简单的模型去直接套用。
Sinusoidal / harmonic model + stochastic model (SpS / Hps)
对上一个模型进行了额外的调整。在这里,stochastic model事实上是stochastic(residual component) model,也就是对residual component进行处理:
[mathjax]yst[n]=\sum_{k=0}^{n-1} u[k]h[n-k][/mathjax]其中,[mathjax]u[n][/mathjax] : white noise ; [mathjax]h[n][/mathjax]:impulse response of residual approximation [mathjax]x[n][/mathjax] .
展示课:
用sms-tools自带的GUI模块分析音频,模型是本章课程的全部5个模型。
编程课:
1,用python实现stochastic model,approximation那块直接使用了scipy.signal.resample(而不是其他更复杂的算法)。
2,用python实现HpR model
3,用python实现HpS model
第8章:Sound Transformation
本章课程初步介绍了一系列有关transformation的操作:
Filter / 滤波器:
这个在数字信号处理课程里出现的更早,且要求更高。本课介绍的滤波器仅仅是一小部分用法:对STFT处理后得到的magnitude spectrum和phase spectrum进行滤波。BPF滤波器、FIR滤波器(在前几章作业里可能会涉及到)在本系列课程里只需要做基本了解。
Morphing
假设我们对输入音频信号A进行STFT处理,得到了STFT(A);我们也对另一个信号B进行了STFT处理,并对处理结果中的每一帧进行smoothing处理(可选用的一些方法),然后与STFT(A)的对应帧相乘。然后再进行常规的ISTFT和overlap-add处理。
Scaling frequency, amplitude and time
在(magnitude / phase)spectrogram上,使用 (frequency, amplitude, time) scaling envelope进行处理,然后再进行常规的ISTFT和overlap-add处理。
第9章:Spectral-based audio features
1,在对输入音频信号进行STFT处理后,我们可以通过进一步分析(magnitude, phase)spectrogram获得这段音频信号的更多特征。有很多特征在音频处理库里非常常见,但在本课程中还是第一次提及,比如:MFCC, chroma .
(以下内容复制自教学资源)
Single-frame spectral features
- Energy, RMS, Loudness
- Spectral centroid
- Mel-frequency cepstral coefficients (MFCC)
- Pitch salience
- Chroma (Harmonic pitch class profile, HPCP)
Multiple-frames spectral features
- Event segmentation, onsets
- Predominant pitch
- Statistics of single-frame features
2,继上一节课“对单个音频特征的分析”后,这节课将分析范畴扩大到音乐集合,也就是分析某一种类的音乐特征。
(level) physical -> sensorial -> perceptual -> formal -> cognitive
从physical level(比如frequency)到cognitive level(比如emothion),抽象程度逐渐提高;在每一个抽象层级,都有若干特征描述术语对应。
3,本系列课程仅仅接触到了音乐特征集合中的很小一部分,大部分都是physical level . 但是我们仍然可以用这些特征进行一些简单的音乐分类:比如计算出frequency、MFCC等特征,然后用简单的统计算法进行处理。比如机器学习基础知识里常见的 Euclidian distance, cosine distance, K-means, KNN .
4,编程作业:本周编程作业不需要写代码实现某种具体算法,而是一个实践题:申请freesound API,然后用已提供的python代码下载一系列音频文件(可以指定这些音频的分类和关键词);从这些音频文件里选出若干组音频,使得这些音频用K-means能够较好地进行区分(clustering).
第10章 Summary
1, beyond this course. 现实中音频、音乐分析所需要的技术、知识,绝大多数都要比本系列课程更进一步(比如第9章提到的各种音乐特征)。
2,computer music 相关的国际会议、论文、资源网站、PhD项目。
补充文章
↑ : ASPMA补充材料(1):DFT、FFT、Minimize energy spread in DFT of sinusoids的python3实现
↑ :ASPMA补充材料(2):(zero) padding, zero phase zero padding