This post was published in 2022-09-04. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
今天从哪里开始?
上一篇笔记(🔗 2022-09-01)提到了还没有学习的地方:

所以本篇笔记内容主要是:离散信号的傅里叶,包括离散周期信号和离散非周期信号。
非周期离散信号的傅里叶变换
P227页开始
直接上公式就好了:
非周期离散信号的傅里叶变换:
[mathjax-d]{\color{red}{X}}(e^{j\omega})=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}[/mathjax-d] [mathjax-d]x[n]=\frac{1}{2\pi}\int_{2\pi}{\color{red}{X}}(e^{j\omega})e^{j\omega n}d\omega[/mathjax-d]对比非周期连续信号的傅里叶变换:
非周期连续信号的傅里叶变换
[mathjax-d]{\color{red}{X}}(j\omega)=\int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt[/mathjax-d] [mathjax-d]x(t)=\sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0 t}=\sum_{k=-\infty}^{+\infty}\frac{1}{T}{\color{red}{X}}(jk\omega_0)e^{jk\omega_0 t}=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\color{red}{X}}(j\omega)e^{j\omega t}d\omega[/mathjax-d]接下来是P229的一些重要内容:

怎么感觉有点陌生呢?
翻出2022-09-01的笔记,发现了不对:

离散周期信号的傅里叶级数表示
所以现在来学习P133:离散时间周期信号的傅里叶级数表示
下面的内容在阐述P133~P134的部分:
首先按照常理,我们应该能写出粗略的一个离散信号的傅里叶级数表达式:
[mathjax-d]x[n]=\sum_{k=-\infty}^{+\infty}a_k e^{jk\omega_0 n}[/mathjax-d]但是上面这个式子并不是很“好”,因为我们注意到离散信号[mathjax]e^{jk\omega_0 n}[/mathjax]有一个神奇的特性:[mathjax]k=k_0[/mathjax]和[mathjax]k=k_0+2\pi[/mathjax](以及[mathjax]k=k_0+4\pi[/mathjax], [mathjax]k=k_0+8\pi[/mathjax] ... )代入[mathjax]e^{jk\omega_0 n}[/mathjax]会得到完全一样的离散信号!
所以我们可以大胆猜想:傅里叶级数表达式中的[mathjax]\sum\limits_{k=-\infty}^{+\infty}[/mathjax]完全没必要写这么多:
[mathjax-d]x[n]=\sum_{k=-\infty}^{+\infty}a_k e^{jk\omega_0 n}=\sum_{k}a_ke^{jk\frac{2\pi}{N}n}[/mathjax-d]可以“看出来”,只需要把[mathjax]k[/mathjax]限定在一个长度为[mathjax]N[/mathjax]的范围内即可!

所以就可以写成:
[mathjax-d]x[n]=\sum_{k=<N>}a_k e^{jk\frac{2\pi}{N}n}[/mathjax-d]接下来看这里:
P134

留了一个 三角函数有限和 的内容没有完全证明 (证明了,写在 🔗 2022-06-09),剩下的就是套公式:
(周期信号傅里叶级数)
[mathjax-d]a_k=\frac{1}{N}\sum_{n=<N>}x[n]e^{-jk\frac{2\pi}{N}n}[/mathjax-d]这里要注意[mathjax]k[/mathjax]和[mathjax]n[/mathjax]不要搞混了。与之对应的是连续信号的表达式:
连续信号的表达式
[mathjax-d]a_n=\frac{1}{T}\int_T x(t)e^{-jn\omega_0 t}dt[/mathjax-d]这两个公式由于一个是连续信号[mathjax]x(t)[/mathjax],一个是离散信号[mathjax]x[n][/mathjax],所以很容易搞混不同公式中的[mathjax]t[/mathjax], [mathjax]n[/mathjax]和[mathjax]k[/mathjax].
周期离散信号的例题
然后做一些有关 周期离散信号 的题:
P135~P136
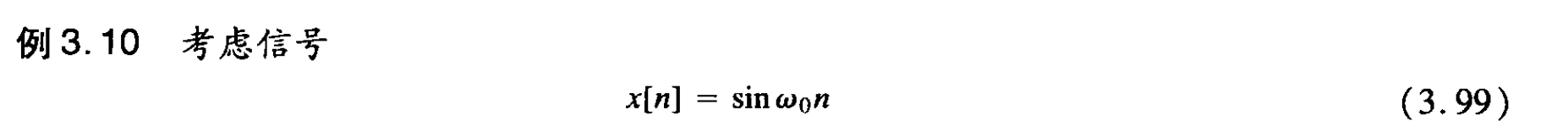
答案:

非周期离散信号的一些总结和例题
学到这里的主要目的是为了明确 周期离散信号的傅里叶级数 大概长什么样。现在知道了:周期离散信号的傅里叶级数以[mathjax]N[/mathjax](基波周期)为周期进行重复。
比如:
P136
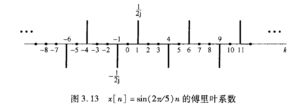
现在回到本篇笔记的开头部分:

所以确实能够理解这部分内容了。
接着P229继续往下看:
有关离散信号在频率为奇数倍[mathjax]\pi[/mathjax]上显得“振荡幅度最高”的问题:

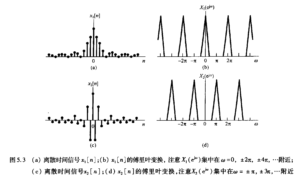
这部分内容在2022-08-25的笔记中也有提及:preview
一些例题
P200
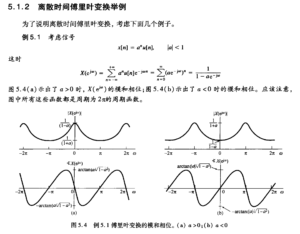
注意这里的复数函数分析:(目前只会用这种方法,我觉得有点臃肿,应该有更简洁的,但我暂时没找到)
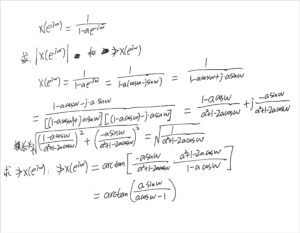
P231
注:没什么难的地方。书中的“无穷几何级数的闭式”其实就是等比数列求和的极限。
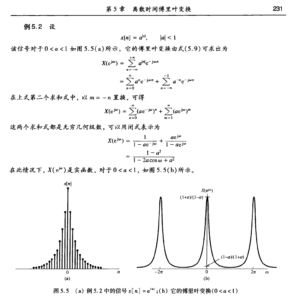
「周期、非周期、离散、连续」4组公式的总结
到目前为止的4组公式总结:
为了防止公式抄错,一律使用书上的截图!
连续周期信号的傅里叶级数
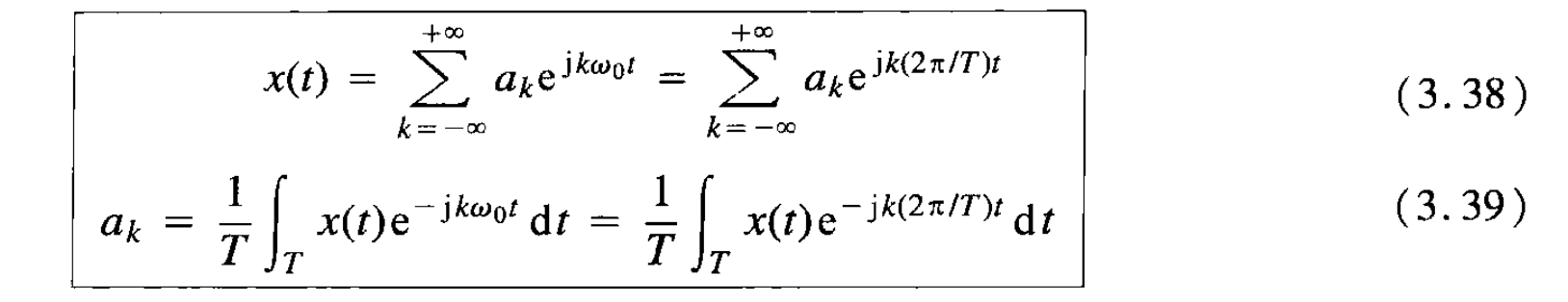
频谱图:离散
离散周期信号的傅里叶级数
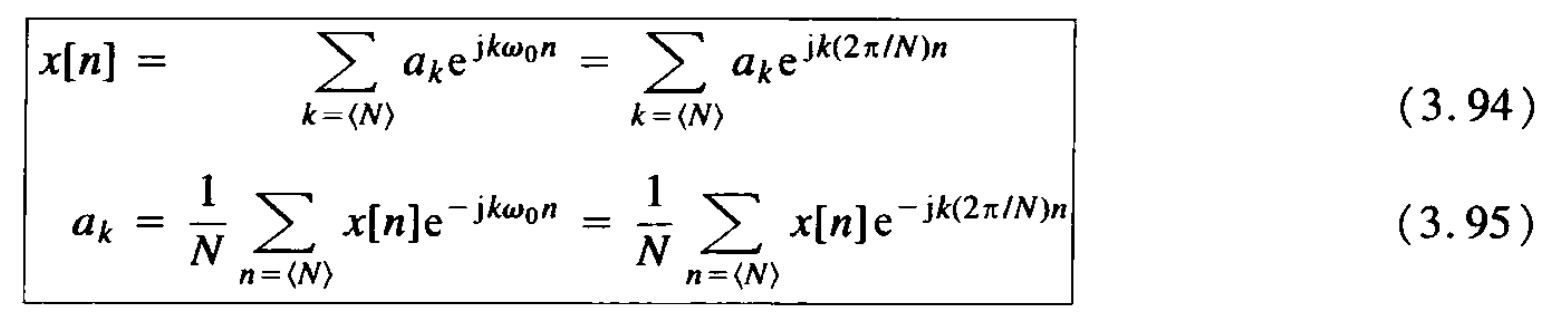
频谱图:离散,以[mathjax]2\pi[/mathjax]为周期
在绝大多数计算机程序里(比如scipy, matlab, librosa),公式(3.94)就是 IDFT ,而(3.95)就是 DFT . 这些程序没办法像人一样去分析 非周期信号-频域连续 这样的数学公式,所以只能假定输入的信号为周期信号(假想输入的信号的前后还有无数个一模一样的信号,这样就变成周期信号了),并且周期信号的周期[mathjax]N[/mathjax]就等于输入信号的长度。如果我们想让计算机程序去近似非周期离散信号的频谱图,就要给输入信号做zero padding,尽可能的增大输入信号的长度,这样就能提高频谱图的分辨率。
连续非周期信号的傅里叶变换
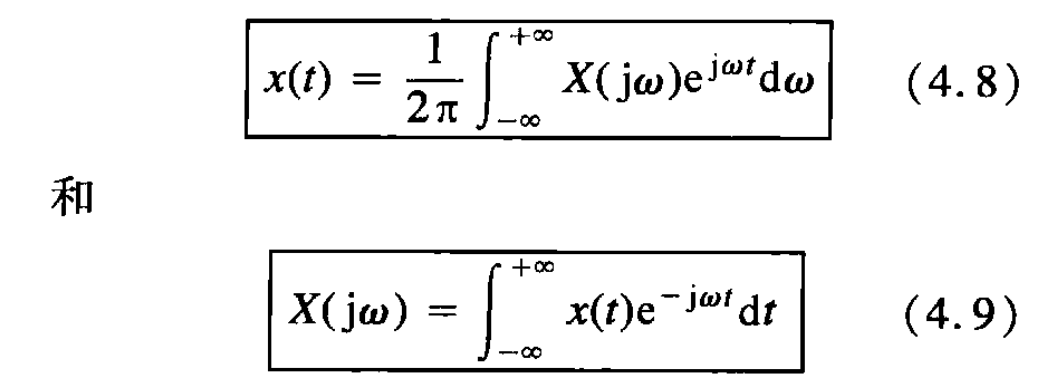
频谱图:连续
离散非周期信号的傅里叶变换
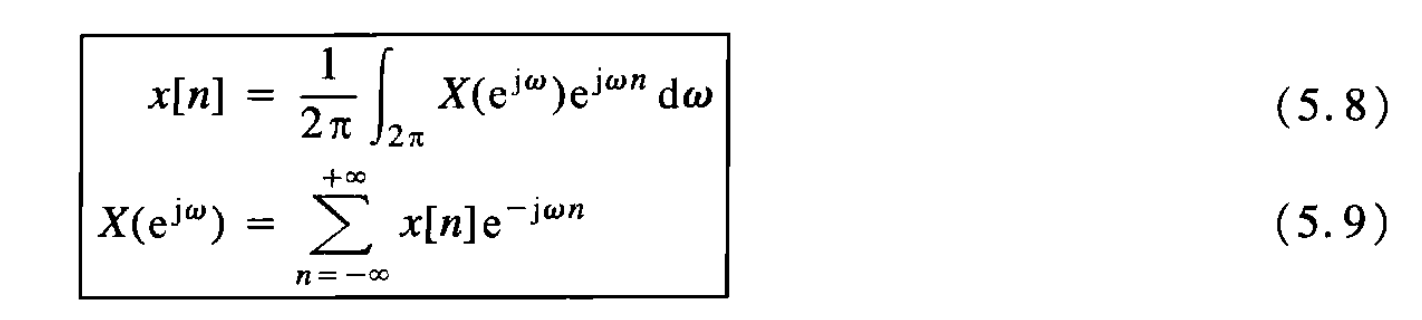
频谱图:连续,以[mathjax]2\pi[/mathjax]为周期
计算机程式的DFT分析
过渡一些以前学过的概念:
有限长离散信号的DFT分析
现在我有一段「有限长的」「离散的」「基于周期信号采样得到的」离散信号,我要对它进行频域分析,会得到什么结果呢?
首先我们根据上面的总结可以推测出:因为是离散信号,所以频谱虽然是无限长的,但必定以[mathjax]2\pi[/mathjax]为周期循环,所以我们只需要画出某个周期内的频谱图即可;因为是非周期信号,所以频域必定连续。
也就是这个:

从理论上来说,我们应该得到(一个[mathjax]2\pi[/mathjax]周期内的)连续频谱图。但现实计算中scipy、matlab这些当然不会给我这些,而是给了我一系列离散的点,比如:来自https://truxton2blog.com/aspma-syllabus-review-supplement-1-dft-fft-energy-spread/ 的这张图。
看起来这就涉及到了一个近似计算的问题!由于上述公式中有无穷项的求和符号[mathjax]\sum\limits_{n=-\infty}^{+\infty}[/mathjax],我们操控计算机“硬算”的时候当然也只能拿到近似值。
注意到信号与系统P229的这段话:

那么,计算机在计算DFT的时候有什么底层原理或者参数吗?以前我从来没注意过这个问题,总是简单地call一波DFT()就完事了,因为DFT()总是会返回给我一系列离散的数值。
似乎并没有。计算机(以scipy dft为例)永远会把我们输入信号的长度[mathjax]N[/mathjax]当作“假想周期信号的[mathjax]T[/mathjax]”,不会出现所谓“计算机替我们计算[mathjax][/mathjax]到[mathjax][/mathjax]的求和”这样的好事。为了手动增大频谱图的分辨率,我们只能上另一个法宝了: zero padding !从理论上来说,zero padding了越多的0,频谱图的分辨率就越高。
基于🔗 [ASPMA补充材料(1):DFT、FFT、Minimize energy spread in DFT of sinusoids的python3实现 - Truxton's blog] https://truxton2blog.com/aspma-syllabus-review-supplement-1-dft-fft-energy-spread/ 的老代码,写了一段程序,测试不同zero padding数值给频谱图带来的变化。
import numpy as np
from scipy.fftpack import fft
from scipy.linalg import dft
import matplotlib.pyplot as plt
import matplotlib as mpl
# dpi和中文字体
mpl.rcParams['figure.dpi'] = 200
plt.rcParams['font.sans-serif'] = ['Source Han Sans']
plt.rcParams['axes.unicode_minus'] = False
def plot_array(x, title):
plt.figure()
plt.title(title)
plt.plot(x, marker='o')
plt.savefig(f'{title}.png')
# plt.show()
def plot_magnitude_spectrum(x, fs, N, title):
# 输入的x为frequency in bins,需要转换为frequency (Hz)
plt.figure()
plt.title(title)
plt.xlabel('Frequency (Hz)')
plt.grid()
plt.stem((np.arange(N) * fs / N), x, markerfmt=" ")
plt.savefig(str(N) + '.png')
# plt.show()
fs = 40
f1 = 2
f2 = 5
N = 120
t = N / fs
tn = np.linspace(0, t, N, endpoint=False)
# 生成Sinewave
x = np.cos(2 * np.pi * f1 * tn) + np.cos(2 * np.pi * f2 * tn)
padding_zeros_size = [0, 20, 100, 500, 1000, 5000]
# plot_array(x, "原始信号x")
for padding_size in padding_zeros_size:
zeros = np.linspace(0, 0, padding_size)
x_pad = np.concatenate((x, zeros), axis=None)
N_pad = N + padding_size
# 计算DFT,使用scipy.linalg dft
mx = np.abs(dft(N_pad) @ x_pad)
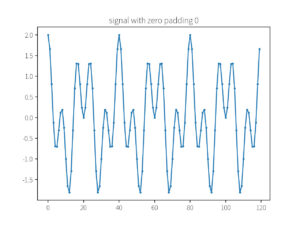
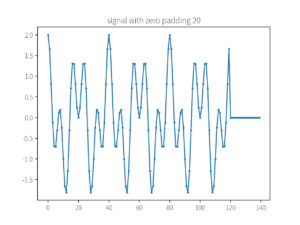
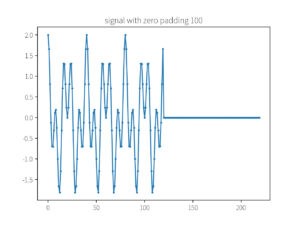
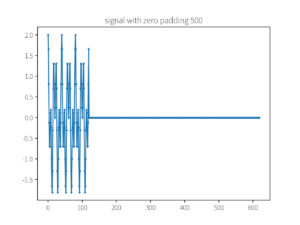
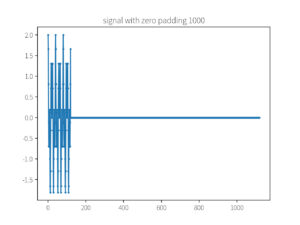
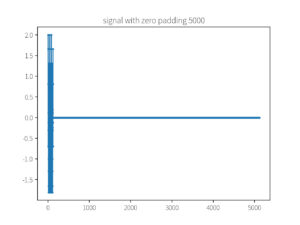
plot_array(x_pad, f'signal with zero padding {padding_size}')
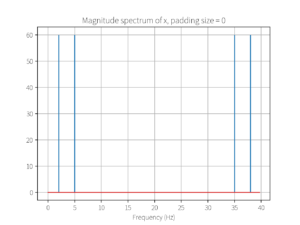
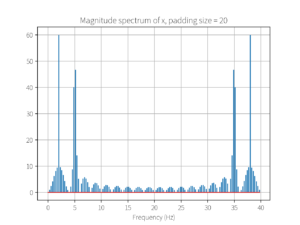
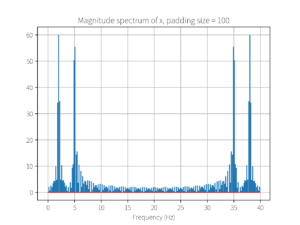
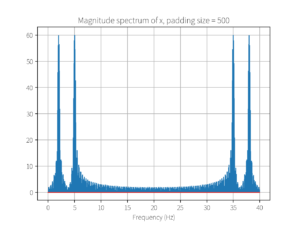
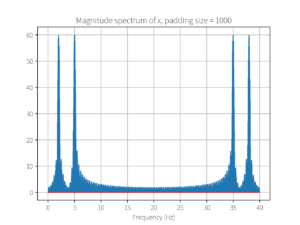
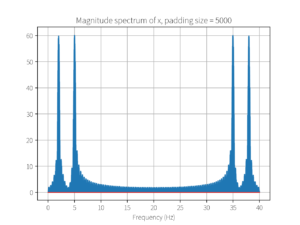
plot_magnitude_spectrum(mx, fs, N_pad, 'Magnitude spectrum of x, padding size = ' + str(padding_size))
运行结果:
但如果我们不搞zero padding,直接把原信号塞到dft()里面进行计算会发生什么呢?如果我们希望计算机给我们计算出周期信号的结果,那么计算机很有可能会瞎猫碰到死耗子(前提是我们塞给计算机[mathjax]N, 2N, 3N \cdots[/mathjax]组数据),这些数据恰好让计算机猜中了周期信号的周期性质。下面的笔记会进一步阐述这方面的内容。
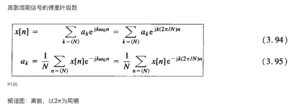
注意到[mathjax]a_k[/mathjax]是离散且周期的,所以我们只需要对[mathjax]n=\langle N\rangle[/mathjax]范围内计算[mathjax]a_k[/mathjax]即可!
这里还有另一个问题:比如我给信号[mathjax]x[n]=\cos(n)[/mathjax]采集了[mathjax]3N[/mathjax]的数据然后送给dft()计算,这种情况下会得到什么结果?答案:会得到一组[mathjax]a_k[/mathjax],但这组[mathjax]a_k[/mathjax]实际上是[mathjax]3[/mathjax]组重复的数据,因为计算机并不知道它计算的是[mathjax]3N[/mathjax]的数据。
计算机程序实际上是怎么计算[mathjax]a_k[/mathjax]的呢?使用矩阵运算。见:preview 🔗 [DFT matrix - Wikipedia] https://en.wikipedia.org/wiki/DFT_matrix
所以说:如果我采集了[mathjax]M[/mathjax]个离散信号数据,不加任何处理就送给dft()进行计算,那么dft()会给我算出一个长度为[mathjax]M[/mathjax]的vector(一维数组,或者说是List)!
当然,如果我们要假惺惺地分析sinusoid信号的频谱图,那么我们就最好生成[mathjax]N, 2N, 3N, \cdots[/mathjax]的数据进行分析,否则会造成频谱泄漏!为什么会泄漏呢?因为你如果不取[mathjax]N[/mathjax]的正整数倍的数据给计算机程序算dft(),计算机在把它“当成”周期信号的时候会把它“当成”另一个周期信号,这个周期信号有“缺口”,这样就发生了频谱泄漏。
(下面这张图画的不是很标准,某些离散的点没标记好)
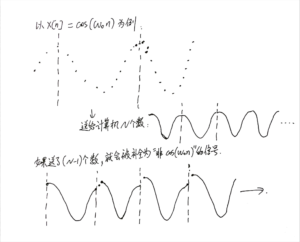
上面这些内容在ASPMA的slide里面也有提到: