WARNING: This article may be obsoleteThis post was published in 2022-10-11. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
又一次记错了harmonic series和octave的关系
又一次记错了harmonic series和octave的关系，再次回顾：
🔗 [2021-12-31 - Truxton's blog] https://truxton2blog.com/2021-12-31/
离散傅里叶变换
公式（来源：奥本海姆《离散时间信号处理》P436~P437）：
[mathjax-d]X[k]=\sum_{n=0}^{N-1}x[n]e^{-jk\frac{2\pi}{N}n}[/mathjax-d]以及
[mathjax-d]x[n]=\frac{1}{N}\sum_{k=0}^{N-1}X[k]e^{jk\frac{2\pi}{N}n}[/mathjax-d]奥本海姆《离散时间信号处理》P436~P437原公式（在符号用法上略有不同）
同时注意到系数[mathjax]\frac{1}{N}[/mathjax]的位置和奥本海姆《信号与系统》P135的不同（本质结果都是一样的）。
使用上面这个公式可以对应熟悉的bin frequency->frequency转换公式。
此外，奥本海姆的书上限定了带波浪线的[mathjax]\tilde{x}[n][/mathjax]是周期信号序列。但我们有的时候也可以“硬用”这个公式，因为有限序列是否周期截断是无从查证的，如果我们硬要说它是周期截断那也没有问题。所以：
如果[mathjax]x[n][/mathjax]是周期序列（对周期信号的周期截断），那么变换后的频谱是符合我们要求的。
如果[mathjax]x[n][/mathjax]不是周期序列（非周期截断，所以我们硬把[mathjax]N[/mathjax]当作它的周期），那么变换后的频谱存在能量泄漏。
研究一下zero-padding问题
我对这篇文章里的zero-padding结论充满了疑惑和怀疑：
🔗 [ASPMA补充材料（2）：(zero) padding, zero phase zero padding - Truxton's blog] https://truxton2blog.com/aspma-syllabus-review-supplement-2-zero-padding-zero-phase/#Zero_padding
现在应该差不多解决了。新结论如下：
参考过的资料：
🔗 [Zero-Phase Zero Padding] https://ccrma.stanford.edu/~jos/sasp/Zero_Phase_Zero_Padding.html
🔗 [fft - Merits of "Zero-Phase" Zero Padding - Signal Processing Stack Exchange] https://dsp.stackexchange.com/questions/18938/merits-of-zero-phase-zero-padding
继续学习傅里叶级数/傅里叶变换的一些性质
从2022-10-08继续，学习傅里叶级数/傅里叶变换的一些性质：
相乘性质
相乘性质
这部分内容应该是很重要的内容才对（和 卷积性质 互补），但暂时没有找到该部分内容在李琳山教授公开课里的对应视频。
这部分内容的证明方法1：
🔗 [如何证明连续时间傅里叶级数的相乘性质？_百度知道] https://zhidao.baidu.com/question/2058873342080339867.html
自己写的方法：
通过观看李琳山老师的视频从头开始复习一些性质
内容1
先放在一边，从这里开始从头复习：
🔗 [10信號與系統 Unit10 Continuous-time Fourier Transform(I)_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1dM4y1M7LK?p=10
看到不熟悉的内容就先记下来
BV1dM4y1M7LK p10 31:00左右
如果有红圈所示的信号[mathjax]x(t)[/mathjax]，这个信号在某一时刻有一个不连续的“断点”（其余部分均为连续），那么对这个信号[mathjax]x(t)[/mathjax]做傅里叶变换，然后又做一次逆傅里叶变换得到[mathjax]x^{\prime}(t)[/mathjax]，那么[mathjax]x^{\prime}(t)[/mathjax]还会是原来那个有断点的信号吗？
不是的。[mathjax]x^{\prime}(t)[/mathjax]会在原来的“断点”处取中间值，然后除了这个断点以外，其余部分均和原有信号[mathjax]x(t)[/mathjax]相同。
从BV1dM4y1M7LK p10 40:10左右开始讲述continous-time fourier transform properties
共轭/conjugate 性质
共轭/conjugate 性质
书P129
或者视频：BV1dM4y1M7LK p10 45:17左右
推导：（第二页纸有点混乱，但基本结果应该是对的）
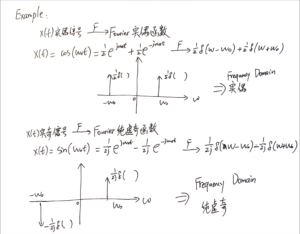
上面只推导了周期连续信号[mathjax]a_k[/mathjax]的情况，非周期连续信号[mathjax]X(j\omega)[/mathjax]的情况应该是基本类似的。
微分和积分
微分和积分
BV1dM4y1M7LK p10 1:00:00左右开始
但在信号与系统的书上暂时没有找到对应的章节
BV1dM4y1M7LK p11 20:00左右开始
时间反转
时间反转
BV1dM4y1M7LK p11 43:55左右开始
这个比 共轭性质 要简单一些。
Duality
Duality
BV1dM4y1M7LK p11 55:16左右开始
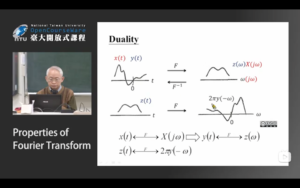
Modulation property
结合Duality和time shift property，我们可以理解这个：Modulation property（注意要把它和time shift区分开来）
modulation：时域乘以某个复指数信号，导致频域shift
time shift：时域shift，频域也shift（本质上频域是乘以某个复指数，但在频域上体现为shift）
应用场景1：调频通讯
这个在视频里有讲，大概意思就是，两个设备进行无线电通讯，需要把各自的设备都调整到某个相同的基准频率[mathjax]\omega_0[/mathjax]上，这样就需要把传进设备的声音讯号频率进行“frequency shift”，然后再进行传输。
应用场景2：音乐转调
卷积性质
卷积性质
再次尝试一下这个！之前乱学了一通，没有完全学会推导过程。
P199
先讨论一下这个：
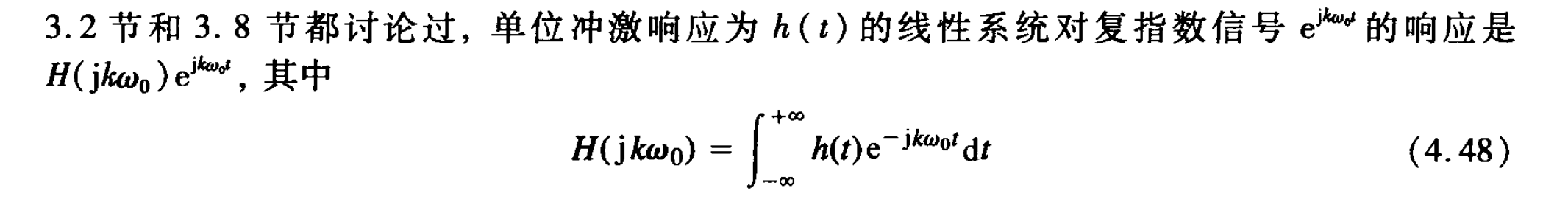
需要复习2022-08-28：
以及2022-08-29：
以及🔗 [2022-09-16 - Truxton's blog] https://truxton2blog.com/2022-09-16/
现在暂时抛开书上使用的LTI系统，证明
[mathjax-d]X(j\omega)Y(j\omega)=x(t)*y(t)[/mathjax-d]现在暂时持有结论： 频域相乘，时域卷积
为了防止老年痴呆忘记LTI系统的一些性质，需要回顾这个例题：
非递归离散时间滤波器
一些例题
非递归离散时间滤波器
例题1（书P150）：有滤波器设计如下：
[mathjax-d]y[n]=\frac{x[n]+x[n-1]}{2}[/mathjax-d]现在要分析这个滤波器对信号产生的效果。
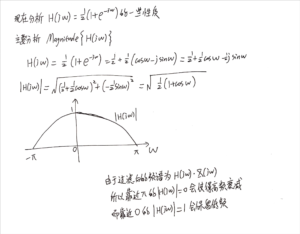
标准答案在书P150：
接下来用类似的方法分析这个滤波器（书P158）：
[mathjax-d]y[n]=\frac{x[n]-x[n-1]}{2}[/mathjax-d]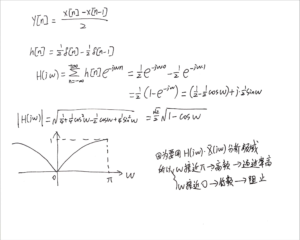
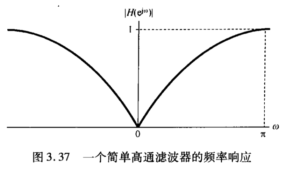
标准答案在书P158~P159：
一些总结
到目前为止学会的 分析滤波器 的方法如下：（连续和离散的情况基本一致，略微修改部分符号即可）
1，想办法得到[mathjax]h(t)[/mathjax]的表达式。上面2道例题可以帮助我们快速学会这个技巧。
2，求[mathjax]h(t)[/mathjax]对应的傅里叶变换表达式：[mathjax]H(j\omega)[/mathjax]
在《信号与系统》中这两个公式分别为3.121和3.122：
[mathjax-d]H(j\omega)=\int_{-\infty}^{+\infty}h(t)e^{-j\omega t}dt[/mathjax-d]以及离散信号版：
[mathjax-d]H(e^{j\omega})=\sum_{n=-\infty}^{+\infty}h[n]e^{-j\omega n}[/mathjax-d]3，得到[mathjax]H(j\omega)[/mathjax]以后，任何通过这个滤波器的信号 的频域 都可以写为[mathjax]H(j\omega)\cdot X(j\omega)[/mathjax] .（[mathjax]X(j\omega)[/mathjax]为原本的信号[mathjax]x(t)[/mathjax]对应的傅里叶变换）
4，绘制出[mathjax]H(j\omega)[/mathjax]对应的模长图[mathjax]\left| H(j\omega) \right|[/mathjax]，然后简单进行分析即可。
比如，这张[mathjax]\left| H(j\omega) \right|[/mathjax]对应的是高通滤波器，这张[mathjax]\left| H(j\omega) \right|[/mathjax]对应的是低通滤波器。
当然，还能从[mathjax]H(j\omega)[/mathjax]反推回[mathjax]h(t)[/mathjax]：
[mathjax-d]h(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}H(j\omega)e^{j\omega t}d\omega[/mathjax-d]本质上和 连续非周期信号的傅里叶逆变换 一样。
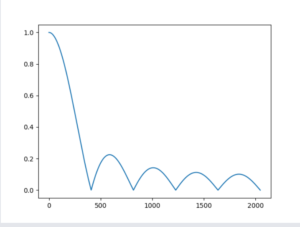
example：
一些代码
import matplotlib.pyplot as plt
import numpy as np
w = np.linspace(0, np.pi, 2048)
h_j_w = 1 / 2 * np.e ** 0 + 1 / 2 * np.e ** (-1j * w * 1)
plt.figure()
plt.plot(np.abs(h_j_w))
plt.show()
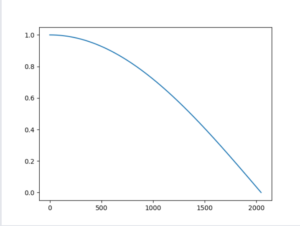
import matplotlib.pyplot as plt
import numpy as np
w = np.linspace(0, np.pi, 2048)
h_j_w = 1 / 3 * np.e ** 0 + 1 / 3 * np.e ** (-1j * w * 1) + 1 / 3 * np.e ** (-1j * w * 2)
plt.figure()
plt.plot(np.abs(h_j_w))
plt.show()
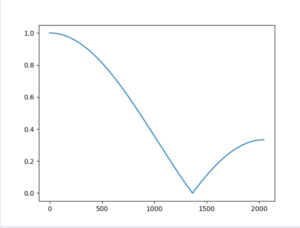
import matplotlib.pyplot as plt
import numpy as np
w = np.linspace(0, np.pi, 2048)
h_j_w = 1 / 4 * np.e ** 0 + 1 / 4 * np.e ** (-1j * w * 1) + 1 / 4 * np.e ** (-1j * w * 2) + 1 / 4 * np.e ** (
-1j * w * 3)
plt.figure()
plt.plot(np.abs(h_j_w))
plt.show()
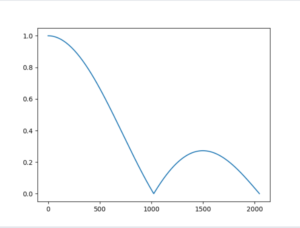
import matplotlib.pyplot as plt
import numpy as np
w = np.linspace(0, np.pi, 2048)
h_j_w = 1 / 10 * np.e ** 0 + 1 / 10 * np.e ** (-1j * w * 1) + 1 / 10 * np.e ** (-1j * w * 2) + 1 / 10 * np.e ** (
-1j * w * 3) + 1 / 10 * np.e ** (-1j * w * 4) + 1 / 10 * np.e ** (-1j * w * 5) + 1 / 10 * np.e ** (
-1j * w * 6) + 1 / 10 * np.e ** (-1j * w * 7) + 1 / 10 * np.e ** (-1j * w * 8) + 1 / 10 * np.e ** (
-1j * w * 9)
plt.figure()
plt.plot(np.abs(h_j_w))
plt.show()
