This post was published in 2022-06-09. Obviously, expired content is less useful to users if it has already pasted its expiration date.
这篇文章鸽了很多内容,其中最重要的“三角函数的正交性”还没来得及继续学就去搞Viterbi了;
这篇文章后面又被补充了大量基础知识基础概念,但“三角函数的正交性”仍然没有学习。
重新复习傅里叶
从离散傅里叶开始推导,但基本跳过连续傅里叶的内容(因为用得少)
Table of Contents
三角函数
🔗 [三角函数公式 - Easymath-wiki] https://easymath-wiki.org/初等数学/三角函数/02三角公式/
主要关注 诱导公式 ,用于下面的DFT计算。比如推导:
[mathjax-d]\cos \left(2 \pi \frac{38 n}{40}\right)=\cos \left(2 \pi n-2 \pi \frac{38 n}{40}\right)=\cos \left(2 \pi \frac{2 n}{40}\right)[/mathjax-d]这是因为
[mathjax-d]\cos(\theta+2k\pi)=\cos(\theta), \cos(-\theta+2k\pi)=\cos(\theta)[/mathjax-d]
和角公式
[mathjax-d]\begin{aligned} &\sin (a+b)=\sin a \cos b+\cos a \sin b \\ &\sin (a-b)=\sin a \cos b-\cos a \sin b \\ &\cos (a+b)=\cos a \cos b-\sin a \sin b \\ &\cos (a-b)=\cos a \cos b+\sin a \sin b \end{aligned}[/mathjax-d]可以用来推导下面的 和差化积、积化和差 .
和差化积、积化和差(可以使用上面的 和角公式 进行推导)
[mathjax-d]\begin{aligned} &\sin \alpha+\sin \beta=2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \\ &\sin \alpha-\sin \beta=2 \cos \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2} \\ &\cos \alpha+\cos \beta=2 \cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \\ &\cos \alpha-\cos \beta=-2 \sin \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2} \end{aligned}[/mathjax-d] [mathjax-d]\begin{aligned} \sin \alpha \cos \beta &=\frac{\sin (\alpha+\beta)+\sin (\alpha-\beta)}{2} \\ \cos \alpha \sin \beta &=\frac{\sin (\alpha+\beta)-\sin (\alpha-\beta)}{2} \\ \cos \alpha \cos \beta &=\frac{\cos (\alpha+\beta)+\cos (\alpha-\beta)}{2} \\ \sin \alpha \sin \beta &=-\frac{\cos (\alpha+\beta)-\cos (\alpha-\beta)}{2} \end{aligned}[/mathjax-d]正弦波信号
特别注意
数字角频率和模拟角频率的2种符号要防止混淆:
本次笔记将同时采用这2种写法。

正弦波信号的前置概念
为了方便理解正弦波信号,先收集足够多的前置概念以免混淆:
最重要的内容
最重要的内容在于对3种频率的理解以及最后的例题
数字信号和模拟信号
模拟信号是连续的,数字信号是离散的
角度(Angle)、弧度(Radian/rad)、转(Turn)
🔗 [弧度 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/弧度
三种频率
(注:本节内容和之后的一些内容有所重复)
模拟频率[mathjax]f[/mathjax]:“每秒时间内信号旋转的圈数” / “信号在1秒内重复的次数”
🔗 [模拟频率与数字频率_deepdsp的博客-CSDN博客数字频率与模拟频率的关系] https://blog.csdn.net/deepdsp/article/details/7272186

模拟角频率[mathjax]\Omega[/mathjax]: “以弧度来表征转的圈数,一圈是[mathjax]2\pi[/mathjax]弧度” 。 所以[mathjax]\Omega=2\pi f[/mathjax].
数字频率:
(目前暂时认为数字频率 = 数字角频率)
“数字频率是对模拟频率的采样,数字频率代表的是两个采样点之间的间隔。“
来自:🔗 [三种频率之间的关系 - 知乎] https://zhuanlan.zhihu.com/p/95429428
周期
🔗 [週期 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/週期
週期(英語:Period)指的是完成往復運動一次所需要的時間,物理學上通常以 T 表示,單位為s。
采样率
🔗 [采样率 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/采样率
采样率(也称为采样速度或者采样频率)定义了每秒从连续信号中提取并组成离散信号的采样个数,它用赫兹(Hz)来表示。采样频率的倒数叫作采样周期或采样时间,它是采样之间的时间间隔。注意不要将采样率与比特率(bit rate,亦称“位元率”)相混淆。
模拟角频率和数字角频率(略有重复)
(目前暂时认为数字频率 = 数字角频率,模拟角频率 = 模拟频率)
最容易理解的来源:🔗 [数字角频率ω与模拟角频率Ω的理解 - 知乎] https://zhuanlan.zhihu.com/p/53664104 来自评论区第一条:

所以模拟角频率:[mathjax]\Omega=2\pi f[/mathjax],单位:rad/s(解释:每秒转动的弧度)
数字角频率:[mathjax]\omega=\frac{2\pi f}{f_s}[/mathjax],单位:rad(解释:两个相邻采样点之间的弧度)
有的时候不同教材不同标准会使用相反的符号来表达这2种角频率,但完全不用担心混淆它们:它们应用的领域是完全不同的,一个是模拟信号/连续信号,另一个是数字信号/离散信号。
模拟频率转换为数字频率
场景:在连续的模拟信号上取样组成离散的数字信号。
例题来自:🔗 [模拟频率与数字频率_deepdsp的博客-CSDN博客数字频率与模拟频率的关系] https://blog.csdn.net/deepdsp/article/details/7272186
假定有一个正弦信号[mathjax]x(t)[/mathjax],频率为[mathjax]f=100Hz[/mathjax],幅度为[mathjax]A[/mathjax],初始相位为0,则这个模拟信号用公式可以表示为:
[mathjax-d]x(t)=A\sin(2\pi 100t)[/mathjax-d]
用采样频率[mathjax]f_s=500Hz[/mathjax]对它进行采样,则得到的数字信号如何用公式表达?
答案
[mathjax-d]x[n]=A\sin(\frac{2\pi f}{f_s})=A\sin(0.4\pi n)[/mathjax-d]在原题中有一个结论:

数字信号的频率确实是[mathjax]0.4\pi[/mathjax],注意这是数字角频率!
复习(该章节存在未解决的问题)
这个slide包含了大部分本次笔记的知识点:🔗 [Discrete-Time Sinusoids] https://www.comm.utoronto.ca/~dkundur/course_info/signals/notes/Kundur_DstTimeSinusoids.pdf
但特别注意,p16/23仍然存在一个没搞明白的内容:
(补充:我猜测这里可能想写的是[mathjax]x_1(t) \perp x_2(t)[/mathjax])
看起来完全不可理喻,反例:🔗 [Finding the intersection of two sinusoids with variable frequency, but only when the intersection occurs on the x-axis?:math] https://www.reddit.com/r/math/comments/1o4k9r/finding_the_intersection_of_two_sinusoids_with/
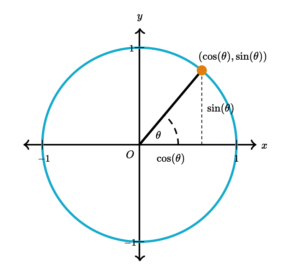
正弦波信号公式
模拟信号
简单来说就是(通常是自然界的)连续的、数学形式上的信号,注意它的写法是[mathjax]y(t)[/mathjax].
🔗 [Sine wave - Wikipedia] https://en.wikipedia.org/wiki/Sine_wave
[mathjax]y(t)=A \sin (2 \pi f t+\varphi)=A \sin (\omega t+\varphi)[/mathjax],且[mathjax]f=\frac{1}{T}[/mathjax]
解释如下:
[mathjax]T[/mathjax]: 周期;

数字信号
简单来说就是通过在模拟信号上采样以后计算机才能对这些离散的信号点进行存储和计算,注意它的写法是[mathjax]y[n][/mathjax].
[mathjax]y[n]=A \sin (\Omega n+\varphi)[/mathjax], [mathjax]\Omega=\frac{2\pi f}{f_s}[/mathjax].
周期换算
🔗 [周期函数 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/周期函数

所以对于这个正弦波 [mathjax]y(t)=A \sin (2 \pi f t+\varphi)=A \sin (\omega t+\varphi)[/mathjax] 而言,[mathjax]f=\frac{1}{T}[/mathjax],因为:
[mathjax-d]\displaylines{ y(t)=A \sin (2 \pi f t+\varphi), \cr \begin{aligned} y(t+T)&=A \sin [2 \pi f (t+T)+\varphi] \\ &=A \sin [2 \pi f (t+\frac{1}{f})+\varphi] \\ &=A \sin (2 \pi f t+2\pi+\varphi) \\ &=A \sin (2 \pi f t+\varphi) \\ &=y(t) \end{aligned} }[/mathjax-d]根据周期的定义可知[mathjax]T=\frac{1}{f}[/mathjax].
图例
用这个例子来确保自己对正弦波的记忆不会出问题:
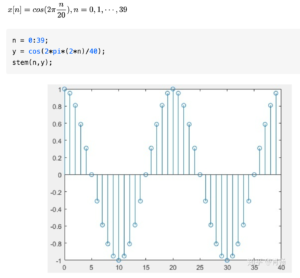
正弦波程序1: 香农采样定理
matlab出了点问题...换python画好了。
仍然基于「如何通俗地解释什么是离散傅里叶变换? - 肖畅的回答 - 知乎 https://www.zhihu.com/question/21314374/answer/542909849」的例题:
下面这个程序需要对比[mathjax]y(n)=\cos(2\cdot \pi \cdot \frac{2}{40} \cdot n)[/mathjax],[mathjax]y(n)=\cos(2\cdot \pi \cdot \frac{38}{40} \cdot n)[/mathjax],以及[mathjax]y(n)=\cos(2\cdot \pi \cdot \frac{4}{40} \cdot n)[/mathjax]
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 40, 1)
f1 = 2 / 40
f2 = 4 / 40
f3 = 38 / 40
y1 = np.cos(2 * np.pi * f1 * t)
y2 = np.cos(2 * np.pi * f2 * t)
y3 = np.cos(2 * np.pi * f3 * t)
plt.figure()
plt.plot(y1)
plt.grid()
plt.title('f=2/40')
plt.savefig('1.png')
plt.figure()
plt.plot(y2)
plt.grid()
plt.title('f=4/40')
plt.savefig('2.png')
plt.figure()
plt.plot(y3)
plt.grid()
plt.title('f=38/40')
plt.savefig('3.png')
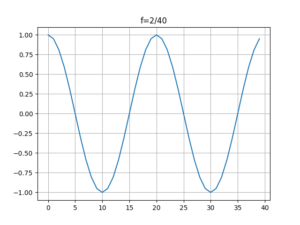
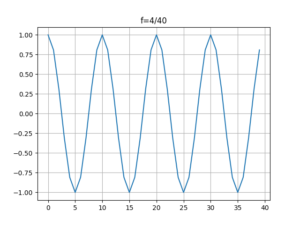
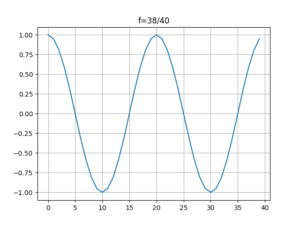
等等,看起来有一点点反直觉,为什么有的时候随着[mathjax]f[/mathjax]的增大,正弦曲线未必会变得密集呢?
呃呃,这玩意首先是 栅栏效应 引起的,随着频率的增加,采样率却没有增加(在这里采样率为定值),导致了严重的栅栏效应。在此之前记录过有关栅栏效应的内容,见:🔗 [ASPMA补充材料(2):(zero) padding, zero phase zero padding - Truxton's blog] https://truxton2blog.com/aspma-syllabus-review-supplement-2-zero-padding-zero-phase/
在继续探讨这个问题之前,首先明确以上代码对应的基本参数:
代码: t = np.arange(0, 40, 1) ,所以每1s采样一个点,40s采样了40个点。根据[mathjax]F_s[/mathjax]的定义: The sampling frequency or sampling rate, fs, is the average number of samples obtained in one second. (来源),所以在这里[mathjax]F_s=1[/mathjax].
我们可能会对[mathjax]f=\frac{20}{40}[/mathjax]感兴趣,是因为:

如果把上面的python程序写全,让它计算[mathjax]\frac{0}{40}\sim\frac{39}{40}[/mathjax],则会看到:
python代码
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 40, 1)
for i in range(0, 40):
f = i / 40
y = np.cos(2 * np.pi * f * t)
plt.figure()
plt.plot(y)
plt.grid()
plt.title('f=%s/40' % i)
plt.savefig('%s.png' % i)
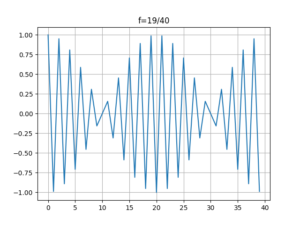
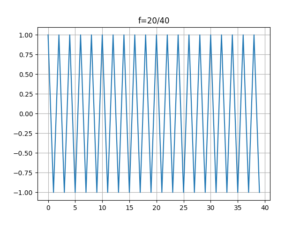
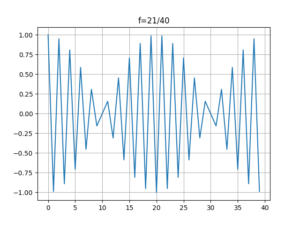
[mathjax]f=\frac{20}{40}[/mathjax]看起来也最为特殊。但它距离「满足香农采样定理」就差一点点。也就是说[mathjax]f=\frac{20}{40}[/mathjax]仍然无法恢复原来的正弦波信号。
参考:🔗 [Why is the Nyquist(Shannon) sampling rate exactly 2 times the maximum frequency? Where is the proof for that constant 2? - Quora] https://www.quora.com/Why-is-the-Nyquist-Shannon-sampling-rate-exactly-2-times-the-maximum-frequency-Where-is-the-proof-for-that-constant-2,这里提到了1个重要的知识:
Because you need at least 3 samples per signal period, to uniquely interpolate the original signal.
又:🔗 [600.457 Lecture Week 3] https://www.cs.jhu.edu/~subodh/457/antialias.html 有一张图:
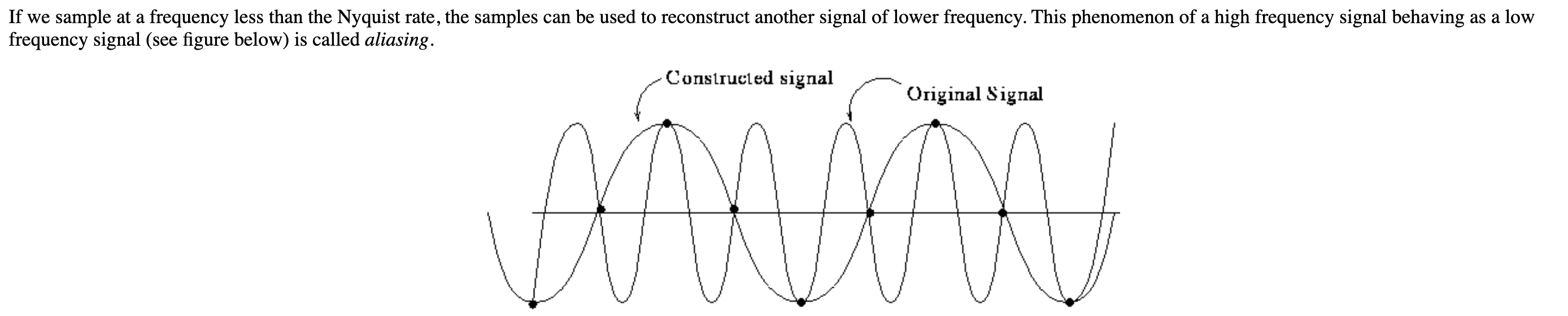
可以看出[mathjax]F_s=2f[/mathjax]确实无法恢复唯一的正弦信号。
另注:上图中「还原信号和原有信号频率不一致」的现象又称为 Aliasing .
三角函数的正交性
扯远了,继续看「如何通俗地解释什么是离散傅里叶变换? - 肖畅的回答 - 知乎 https://www.zhihu.com/question/21314374/answer/542909849」的例题:
这里遇到了很多问题,首先要解决的就是「三角函数的正交性」:
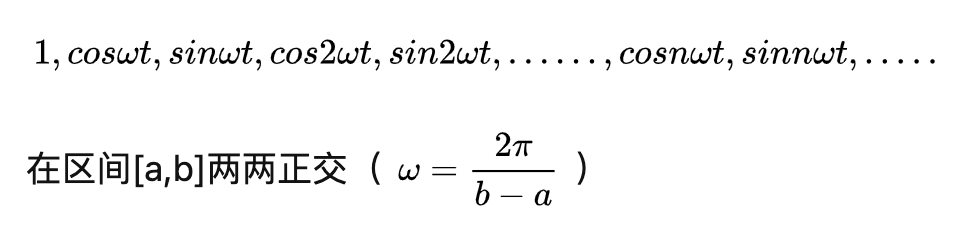
更确切地描述:

只要使用 积化和差 即可证明(积化和差公式写在本笔记前面:preview)。网上有很多教学资源,比如:🔗 [三角函数正交性的推导_码农u号的博客-CSDN博客三角函数正交性] https://blog.csdn.net/qq_29545231/article/details/108547437,或者:🔗 [Microsoft Word - Summary 259.doc] https://ocw.chu.edu.tw/pluginfile.php/861/mod_resource/content/14/Summary_259.pdf
推导过程中涉及的关键步骤:

三角形的正交性变体—奇怪的离散版本
我也不知道最开始我是怎么从三角函数正交性推导到这里来的:

现在是2022-08-26,距离2022-06-09的笔记已经过去了一段时间。我自己都忘了当时是从哪里看到这个公式的,总之,我们现在有:
[mathjax-d]\sum_{t=0}^{M-1}\cos(2\pi \frac{N}{M}t)=0; 0< N< M, M>=2[/mathjax-d]比如:
[mathjax-d]\sum_{t=0}^{39}\cos(2\pi \frac{7}{40}t)=0[/mathjax-d]或者
[mathjax-d]\sum_{t=0}^{39}\cos(2\pi \frac{17}{40}t)=0[/mathjax-d]一段佐证程序:
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 40, 1)
f1 = 14 / 40
y = np.cos(2 * np.pi * f1 * t)
f2 = 7 / 40
y2 = np.cos(2 * np.pi * f2 * t)
pro = y * y2
plt.figure()
plt.grid()
# plt.plot(y)
# plt.plot(y2)
plt.plot(pro, marker=".")
plt.savefig('1.png')
print(np.dot(y, y2))
第16行得到:
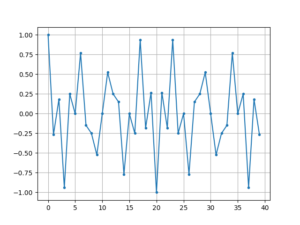
第19行得到: 1.4432899320127035e-15 .
上面这张图起码还能看出个大概(有很明显的轴对称关系),也很容易证明,但把程序里的40改成19这样的奇数就恶心很多了:
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 39, 1)
f1 = 14 / 19
y = np.cos(2 * np.pi * f1 * t)
f2 = 7 / 19
y2 = np.cos(2 * np.pi * f2 * t)
pro = y * y2
plt.figure()
plt.grid()
# plt.plot(y)
# plt.plot(y2)
plt.plot(pro, marker=".")
plt.savefig('1.png')
print(np.dot(y, y2))第15行得到: -1.2365108936762681e-14
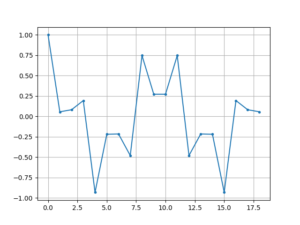
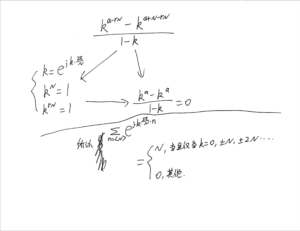
证明方法:用欧拉公式展开,求等比数列的和,并利用[mathjax]e^{j2\pi N}=1[/mathjax](N是整数)这个重要的性质。
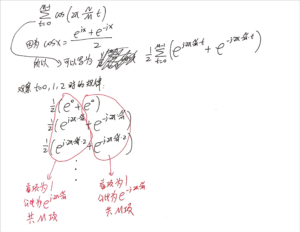

其他思路可以参考: 🔗 [Limit of series involving sum of cosines $\lim_{n \to \infty} \sum_{k=0}^{n} \cos(\frac{2k\pi}{n})$ - Mathematics Stack Exchange] https://math.stackexchange.com/questions/4136552/limit-of-series-involving-sum-of-cosines-lim-n-to-infty-sum-k-0n-co

(继续上面的内容)三角函数的有限和
* 下面的内容是2022-09-10补充的。
* 有关三角函数有限和的拓展阅读:🔗 [三角函数基本关系和公式 | Fan's Math World] https://fanhongtao.github.io/math/san-jiao-han-shu-ji-ben-guan-xi-he-gong-shi.html
一直没搞明白当时我是如何莫名其妙推导到这个公式的:
[mathjax-d]\sum_{t=0}^{M-1}\cos(2\pi \frac{N}{M}t)=0; 0< N< M, M>=2[/mathjax-d]直到后来我看到奥本海姆信号与系统P134:

好像很类似!当然,上面那个公式只是一种特殊情况,现在继续上面的公式,把它写成一个更一般的公式(暂时先抛开奥本海姆的公式):
[mathjax-d]\sum_{t=0}^{M-1}\cos(2\pi \frac{N}{M}t)=0; 0< N< M, M>=2[/mathjax-d]这个公式推导起来就要比前面那个特殊情况下的公式要难一些了。特殊情况下的公式推导见本笔记前面。
推导如下:


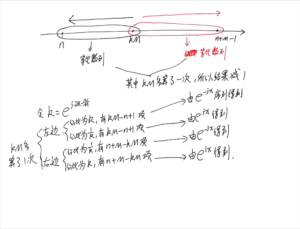


现在再用相同的思路推导奥本海姆书上的公式(思路一样,只是写法略有不同,所以下面的推导步骤比较简略)