This post was published in 2021-07-02. Obviously, expired content is less useful to users if it has already pasted its expiration date.
本文是对ASPMA课程大纲复习的补充。
所有实现代码均为python3;不需要引入sms-tools相关的libs .
相关内容:
● 生成正弦波
● 使用scipy.linalg dft()计算并绘制magnitude spectrum
● 使用scipy.fftpack fft()计算并绘制magnitude spectrum
● 为了防止截断信号时发生频谱能量泄漏(energy spread),需要计算出合适的采样次数N
● 在python3中实现对GCD(float, float)的精确计算
● 对上一步的截断结果进行DFT分析,绘制magnitude spectrum
● energy spread计算出的采样次数N 与 FFT frequency resolution的关联
Table of Contents
DFT、FFT
dft使用scipy.linalg进行计算: mx = np.abs(dft(x.shape[0]) @ x) ;fft使用scipy.fftpack fft进行计算(实际在下列代码中仍然用dft算): mx = np.abs(fft(x)) .
一般还需要对计算结果mx进行Amplitude scaling处理:
mx=mx*2/N , N为原始信号的长度. (即使是后续做了zero-padding,N也不会因zero-padding的参数而发生改变)
需要注意:
1,无论是dft()还是fft(),直接计算出的结果都是frequency bins形式,需要进行换算:
[mathjax-d]n^{th}\ \text{bin(Hz)}=n*\frac{\text{Sampling frequency}}{\text{DFT Size}}[/mathjax-d]2,尽管FFT的计算需要输入的信号长度为2的整数幂,但scipy.fftpack fft()也能接受其他信号长度(这种情况下scipy会调用dft进行计算,导致计算效率大幅度降低)
代码:
import numpy as np
from scipy.fftpack import fft
from scipy.linalg import dft
import matplotlib.pyplot as plt
import matplotlib as mpl
# dpi和中文字体
mpl.rcParams['figure.dpi'] = 200
plt.rcParams['font.sans-serif'] = ['Source Han Sans']
plt.rcParams['axes.unicode_minus'] = False
def plot_array(x, title):
plt.figure()
plt.title(title)
plt.plot(x)
plt.show()
def plot_magnitude_spectrum(x, fs, N, title):
# 输入的x为frequency in bins,需要转换为frequency (Hz)
plt.figure()
plt.title(title)
plt.xlabel('Frequency (Hz)')
plt.grid()
plt.stem((np.arange(N) * fs / N), x)
plt.show()
fs = 40
f1 = 2
f2 = 5
N = 120
t = N / fs
tn = np.linspace(0, t, N, endpoint=False)
# 生成Sinewave
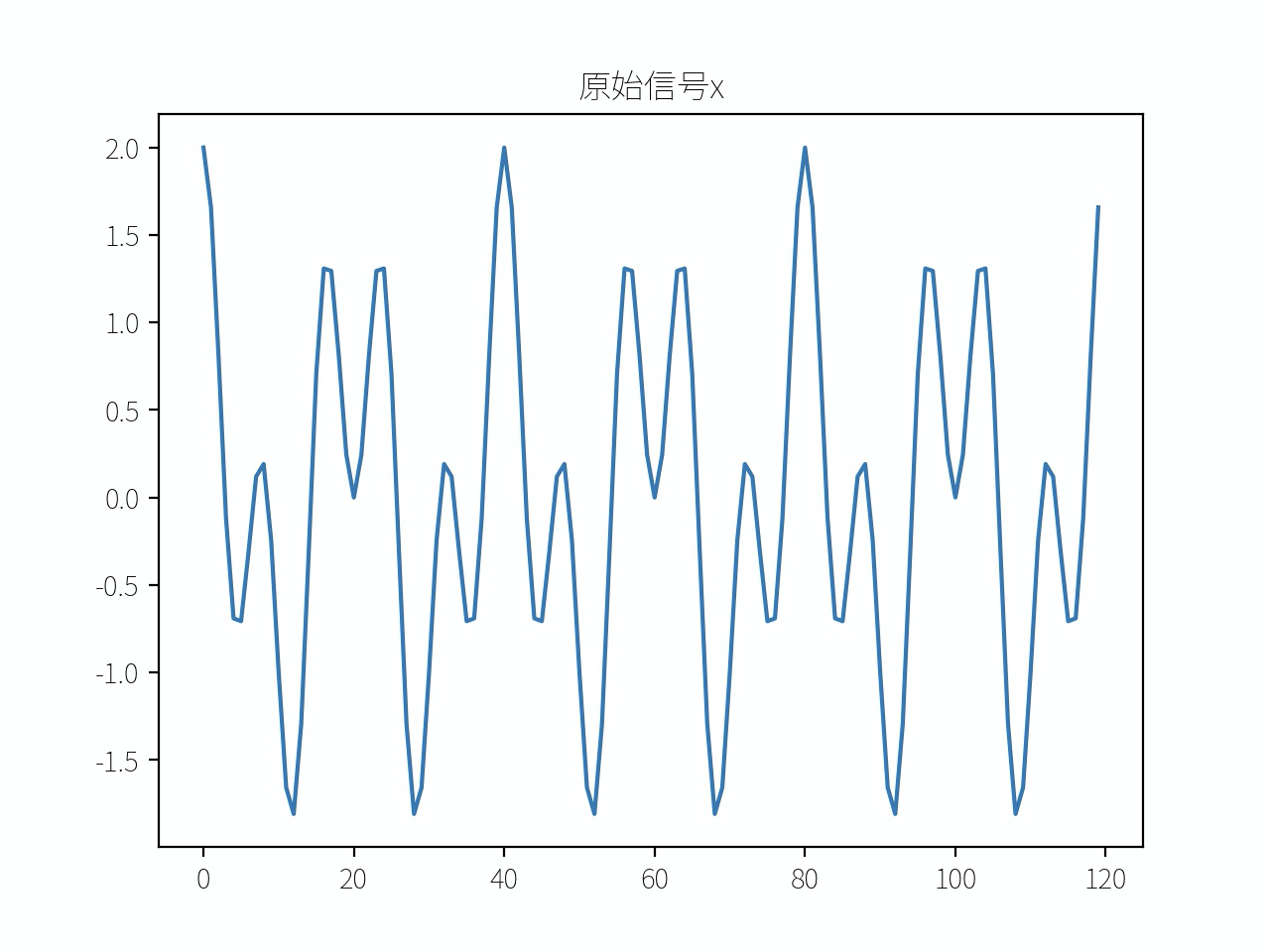
x = np.cos(2 * np.pi * f1 * tn) + np.cos(2 * np.pi * f2 * tn)
# 计算DFT,使用scipy.linalg dft
plot_array(x, "原始信号x")
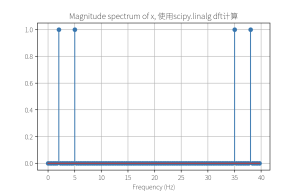
mx = np.abs(dft(N) @ x)
# amplitude scaling
mx = mx * 2 / N
plot_magnitude_spectrum(mx, fs, N, 'Magnitude spectrum of x, 使用scipy.linalg dft计算')
# 计算FFT(事实上仍然是计算DFT)
mx_fft_x = np.abs(fft(x))
# amplitude scaling
mx_fft_x = mx_fft_x * 2 / N
plot_magnitude_spectrum(mx_fft_x, fs, N, 'Magnitude spectrum of x, 使用scipy.fftpack fft计算')
结果:
Fraction in Python
Minimize energy spread in DFT of sinusoids,在截断信号的时候选取合适的采样点数N,防止“非周期截断”,计算公式:
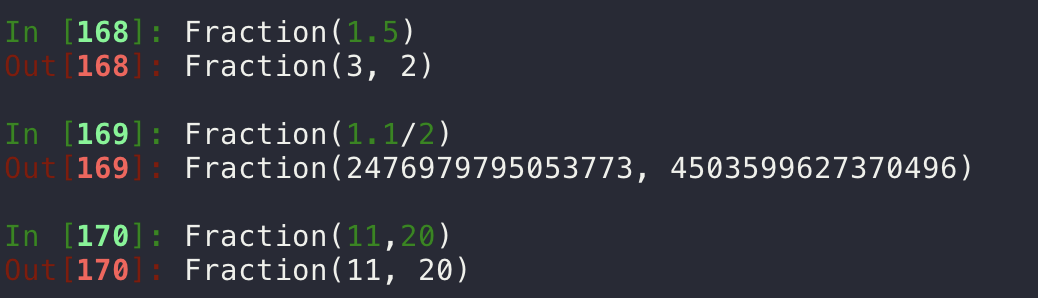
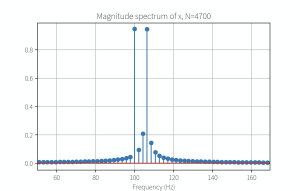
[mathjax-d]N=\frac{\frac{F_s}{f1}*\frac{F_s}{f2}}{GCD(\frac{F_s}{f1},\frac{F_s}{f2})}[/mathjax-d]这里的GCD()的代码实现可能会严重影响最终结果。考虑到python 3.x丢弃了fraction.gcd(),而math.gcd()只允许输入整数,如果暴力使用int(fs/f1)这样的代码,就有可能导致小数点误差被放大。在本文后续举例的代码中,fs=10000, f1=100, f2=106,使用两种计算方法得到的结果分别是N=4700和N=5000(精确)。
所以我们需要计算GCD(float, float)。python提供了2种计算方法: math.gcd() 和 from fractions import gcd; gcd() . 不幸的是,在python 3.x中,fractions gcd()被弃用了(在python 3.7这样稍微早一些的版本里还能导入,只是会有warning);而math.gcd()只接收整数输入。
即使强制使用fractions gcd(),我们也需要把float类型全部转换为符合规范的分数类型,才能得到正确的答案。fractions gcd()对于输入类型要求很严格,比如:
为了避免出现奇奇怪怪的结果,我们需要将每一个分数的分子分母都变成整数,就像这样:
[mathjax-d]\frac{2.075}{205}=\frac{2075}{205000}[/mathjax-d]最后,为了去掉python 3.x的警告,我们可以把fraction gcd()的源代码复制过来用。
代码如下:
import math
from fractions import Fraction
# 直接从python源代码里复制过来的
def gcd(a, b):
if type(a) is int is type(b):
if (b or a) < 0:
return -math.gcd(a, b)
return math.gcd(a, b)
while b:
a, b = b, a % b
return a
# 一个不精确的计算方法
def rough_N(fs, f1, f2):
f1n = int(fs // f1)
f2n = int(fs // f2)
N = int((f1n * f2n) / (math.gcd(f1n, f2n)))
print('这个结果可能不是精确计算结果:N = ' + str(N))
# 可以输入整数、浮点数;如果真的要输入分数(真的会有人这么做吗?),要使用Fraction(a,b),而不是a/b
fs = 10000
f1 = 100
f2 = 106
rough_N(fs, f1, f2)
# 小数点后的位数,用于计算需要多少个10相乘。比如1.005就需要乘以1000变成1005
decimal_fs = 0
decimal_f1 = 0
decimal_f2 = 0
if not isinstance(fs, Fraction):
fs = float(fs)
decimal_fs = len(str(fs).split('.')[1])
if not isinstance(f1, Fraction):
f1 = float(f1)
decimal_f1 = len(str(fs).split('.')[1])
if not isinstance(f2, Fraction):
f2 = float(f2)
decimal_f2 = len(str(fs).split('.')[1])
# 分子分母都需要变成整数,所以需要同乘以较大的系数,1.15/10.5需要变成115/1050,而不是11.5/105
frac1 = Fraction(int(fs * max(decimal_fs, decimal_f1)), int(f1 * max(decimal_fs, decimal_f1)))
frac2 = Fraction(int(fs * max(decimal_fs, decimal_f2)), int(f2 * max(decimal_fs, decimal_f2)))
N_min = (frac1 * frac2) / (gcd(frac1, frac2))
print('精确结果:N = ' + str(N_min))
运行这段代码能得到:
“这个结果可能不是精确计算结果:N = 4700;精确结果:N = 5000”
我们可以尝试用FFT的这段代码验证这个结果,很容易就发现N=4700存在明显的频谱能量泄漏:
FFT frequency resolution
根据上文的代码,如果有正弦波及采样率如下:
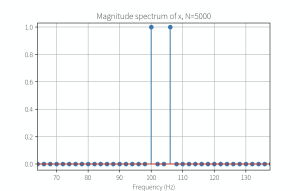
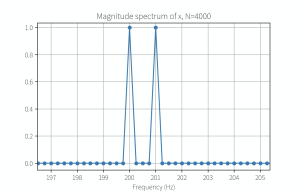
[mathjax-d]x=\cos(2\pi \times 200 t)+\cos(2\pi \times 201 t)\ ,\ F_s=1000H_z[/mathjax-d]那么可以用代码得出(或者手动算出),为了防止频谱能量泄漏,需要的最小采样次数为N=1000。如果在绘制频谱图的时候不使用matplotlib-stem(茎图/棉棒图/杆状图),而是使用常规的折线图,就会得出这个结果:
要进行缩放才能找到:
这个结果也许并不是我们想要的,所以我们可能需要考虑取更多的样本,比如2N, 3N, 4N...
取N个样本就一定会会导致上图所示的结果吗?并不是的。比如这个例子:
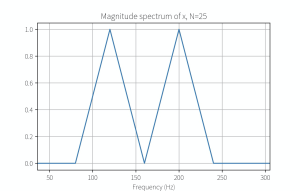
[mathjax-d]x=\cos(2\pi \times 200 t)+\cos(2\pi \times 120 t)\ ,\ F_s=1000H_z[/mathjax-d]计算出N=25,取N个样本计算出的频谱图如下:
这个结果可能是我们想要的。
注意:经过zero-padding处理后的信号不能直接套用下面的判断方法
事实上,当我们在计算出最小采样次数N以后,就可以用一个简单的计算公式来提前预知我们需要用N个采样点,还是2N, 3N...个采样点,来绘制频谱图。
[mathjax-d]\text{FFT\ frequency\ resolution}=\triangle R_{FFT}=\frac{F_s}{N}[/mathjax-d] [mathjax-d]k=\frac{N(\text{to\ minimize\ energy\ spread\ })}{\triangle R_{FFT}}-1[/mathjax-d]计算得到的[mathjax]k[/mathjax]就是两个峰值频率点之间的0幅值点的个数。
比如在上一个正弦波例子中,fs=1000, f1=200, f2=120, FFT frequency resolution=[mathjax]\frac{25}{2}[/mathjax], k=1,意味着频谱图中两个频率节点之间有1个幅值为0的点,所以使用采样数N绘制频谱图就可以得出我们想要的结果(更多采样点数当然也可以)。
而在前一个正弦波例子中,fs=1000, f1=200, f2=201, FFT frequency resolution=1000, k=0,意味着频谱图中两个频率节点之间没有幅值为0的点,我们可能要让采样点数[mathjax]\geq[/mathjax]2N才能得到想要的频谱图: