This post was published in 2021-07-11. Obviously, expired content is less useful to users if it has already pasted its expiration date.
本文是对ASPMA课程大纲复习的补充。
Table of Contents
ASPMA zero phase windowing
ASPMA的所有课程以及作业,都紧密围绕sms-tools -> dftModel.py来进行;dftModel.py里的那一段dft-synthesis以及dft-analysis代码总会被反复利用;“zero phase windowing”也成为这一系列课程中处理语音信号一定会涉及到的一个操作。
事实上,如果要在搜索引擎里更好地找到“zero phase windowing”,也许还应该搜索“zero phase zero padding”。它的重要流程大致如下:
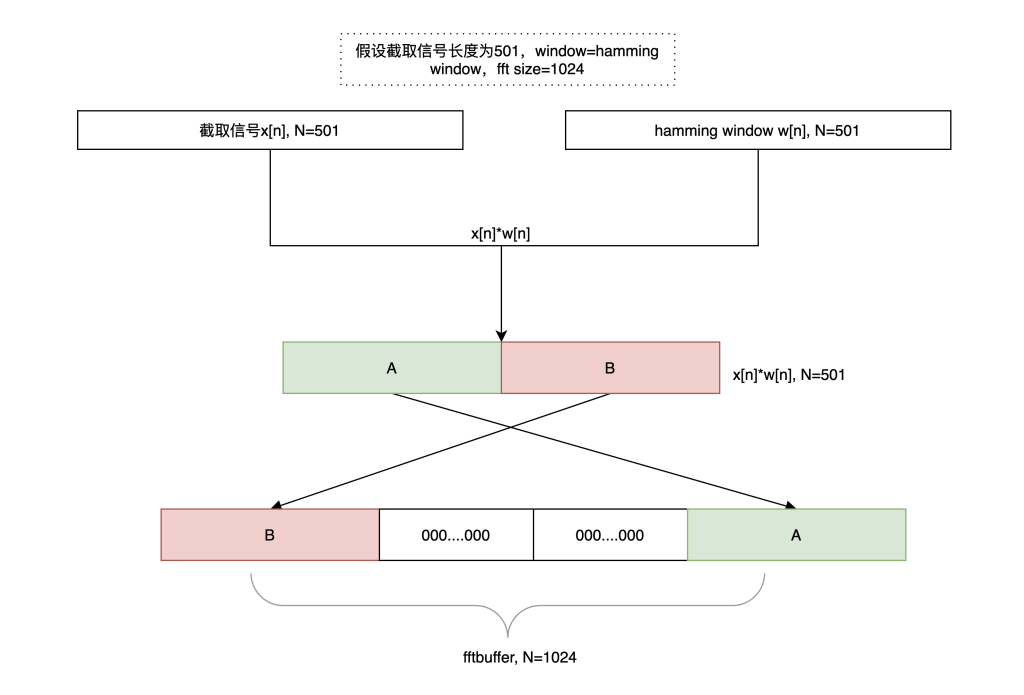
首先截取一段信号x[n]进行分析:
在实际应用中,我们几乎不可能让STFT的每一次截断都恰好截取周期为T的一段信号,所以我们需要用窗函数(比如这里的hamming window)与截取的信号相乘,使得信号的起始点、末尾点的相位[mathjax]\rightarrow[/mathjax]0 ,最大程度降低频谱泄漏的影响;
然后我们需要对信号x[n]*w[n]进行zero-padding处理,使得处理后的信号长度为2的指数次幂([mathjax]N=2^{n}[/mathjax]),使得每次DFT计算都能用FFT进行处理,提高运算效率;
这里的zero-padding也可以称之为zero phase zero padding,因为它能够最大程度让信号fftbuffer成为一个实偶信号(real and even signal)。严格的实偶信号经过离散傅里叶变换得到的结果里,所有复数的系数均为0或者[mathjax]\pm \pi[/mathjax],比如:
[mathjax-d]DFT([0,1,2,1])=[ 4.-0.j, -2.+0.j, 0.-0.j, -2.-0.j][/mathjax-d]当然,判断一个信号为even的条件也很苛刻:
[mathjax-d]X[n]=X[N-n], 1\leq n \leq N[/mathjax-d]判断信号为real的条件则为:
[mathjax-d]X[n]=X[N-1-n], 0\leq n \leq N[/mathjax-d]当然,实际分析音频信号的时候肯定是无法满足这一点的。
Zero padding
* 下面的这部分内容讨论不同zero-padding方法对magnitude spectrum的影响(不讨论phase spectrum).
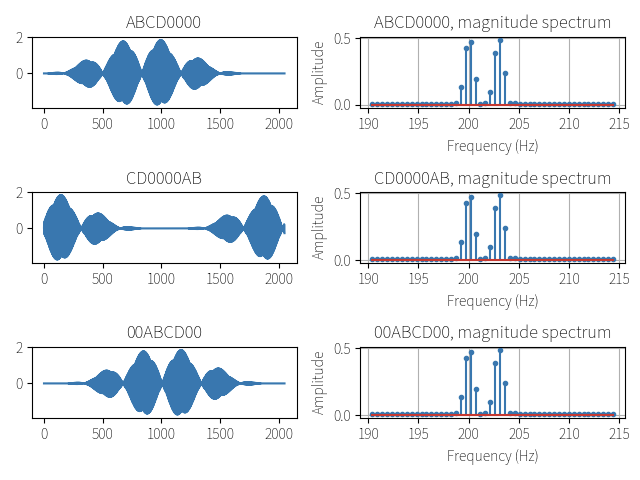
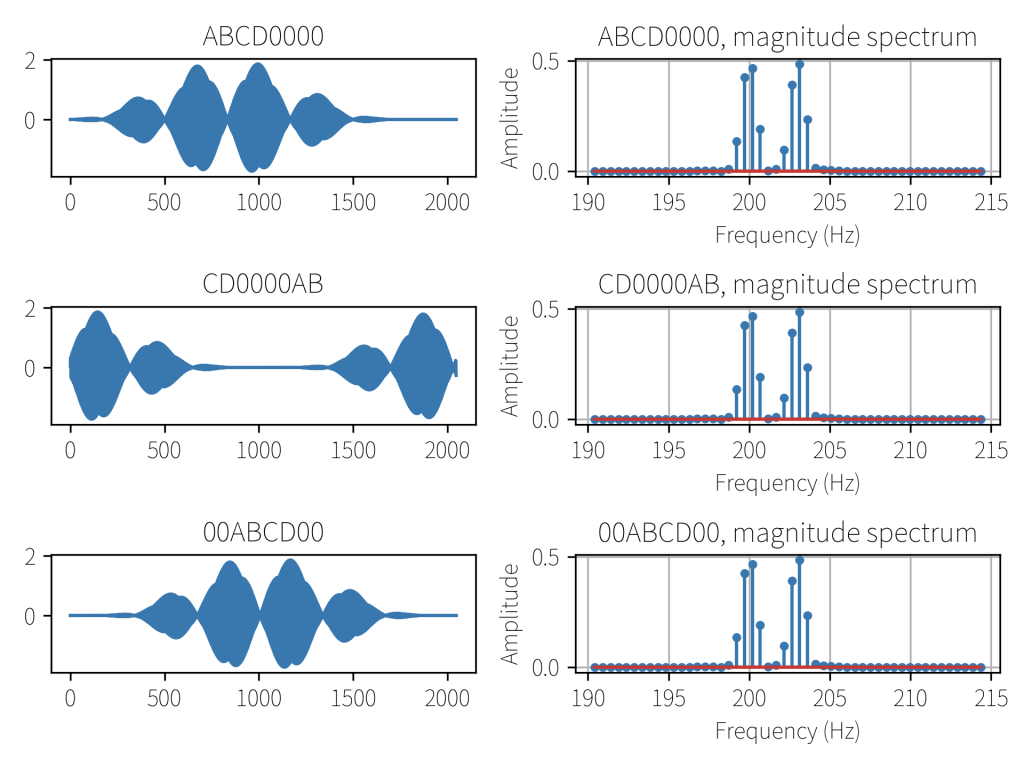
假定一段离散信号采样被标记为 signal ,那么以下几种zero-padding的方法得到的magnitude spectrum都是一样的(注意:下面这些zero-padding得到的[mathjax]N[/mathjax]都是一样的)
方法1: signal00000
方法2: 00000signal
方法3: 00signal000
方法4: nal00000sig
方法5: al00000sign
....(等等)
有限长度的离散傅里叶变换会假定输入序列长度[mathjax]N[/mathjax]就是补全后假想的周期信号的周期[mathjax]N[/mathjax]. 所以只要在输入采样的前后补充无数个相同的序列,在无限时间序列上构成这个样子:
000...00000signal00000signal00000signal00000signal...000
...就会得到相同的magnitude spectrum。
import numpy as np
from scipy.fftpack import fft
from scipy.signal import get_window
import matplotlib.pyplot as plt
import matplotlib as mpl
# dpi和中文字体
mpl.rcParams['figure.dpi'] = 300
plt.rcParams['font.sans-serif'] = ['Source Han Sans']
plt.rcParams['axes.unicode_minus'] = False
def plot_magnitude_spectrum(x, fs, N, title):
plt.title(title)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()
# 这里局部放大了magnitude spectrum
markerline, stemlines, baseline = plt.stem((np.arange(N) * fs / N)[195 * 2:220 * 2], x[195 * 2:220 * 2])
markerline.set_markersize(3)
def op1():
x_fft = np.zeros(N_fft)
x_fft[:N] = x
plt.subplot(321)
plt.title('ABCD0000')
plt.plot(x_fft)
mx_fft_x = np.abs(fft(x_fft))
mx_fft_x = mx_fft_x * 2 / (N)
plt.subplot(322)
plot_magnitude_spectrum(mx_fft_x, fs, N_fft, 'ABCD0000, magnitude spectrum')
def op2():
x_fft = np.zeros(N_fft)
hm1 = (N + 1) // 2
hm2 = N // 2
x_fft[:hm1] = x[hm2:]
x_fft[-hm2:] = x[:hm2]
plt.subplot(323)
plt.title('CD0000AB')
plt.plot(x_fft)
mx_fft_x = np.abs(fft(x_fft))
mx_fft_x = mx_fft_x * 2 / (N)
plt.subplot(324)
plot_magnitude_spectrum(mx_fft_x, fs, N_fft, 'CD0000AB, magnitude spectrum')
def op3():
x_fft = np.zeros(N_fft)
n_padding = (N_fft - N) // 2
x_fft[n_padding:n_padding + N] = x
plt.subplot(325)
plt.title('00ABCD00')
plt.plot(x_fft)
mx_fft_x = np.abs(fft(x_fft))
mx_fft_x = mx_fft_x * 2 / (N)
plt.subplot(326)
plot_magnitude_spectrum(mx_fft_x, fs, N_fft, '00ABCD00, magnitude spectrum')
if __name__ == '__main__':
fs = 1000
f1 = 200
f2 = 203
N = 1701
N_fft = 2048
t = N / fs
tn = np.linspace(0, t, N, endpoint=False)
# 生成Sinewave
x = np.cos(2 * np.pi * f1 * tn) + np.cos(2 * np.pi * f2 * tn)
w = get_window('hann', N)
x = x * w
op1()
op2()
op3()
plt.tight_layout()
plt.savefig('savefig.png')
运行结果:
“栅栏效应“ / Picket Fence Effect
import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
import matplotlib as mpl
# dpi和中文字体
mpl.rcParams['figure.dpi'] = 300
plt.rcParams['font.sans-serif'] = ['Source Han Sans']
plt.rcParams['axes.unicode_minus'] = False
fs = 100
f1 = 2
f2 = 3
N = 80
N2 = 800
t = N / fs
tn = np.linspace(0, t, N, endpoint=False)
# 生成Sinewave
x = np.cos(2 * np.pi * f1 * tn) + np.cos(2 * np.pi * f2 * tn)
plt.figure(1)
mx = np.abs(fft(x))
# amplitude scaling
mx = mx * 2 / (N)
plt.subplot(211)
plt.title('Magnitude spectrum of x, N=80, "栅栏效应"')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()
plt.stem((np.arange(N) * fs / N)[0:5], mx[0:5])
x_padding = np.zeros(N2)
x_padding[:N] = x
mx_padding = np.abs(fft(x_padding))
# amplitude scaling
mx_padding = mx_padding * 2 / (N)
plt.subplot(212)
plt.title('Magnitude spectrum of x,N=800, zero padding')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()
plt.stem((np.arange(N2) * fs / N2)[0:int(5 * N2 / fs)], mx_padding[0:int(5 * N2 / fs)])
plt.tight_layout()
plt.savefig('savefig.png')
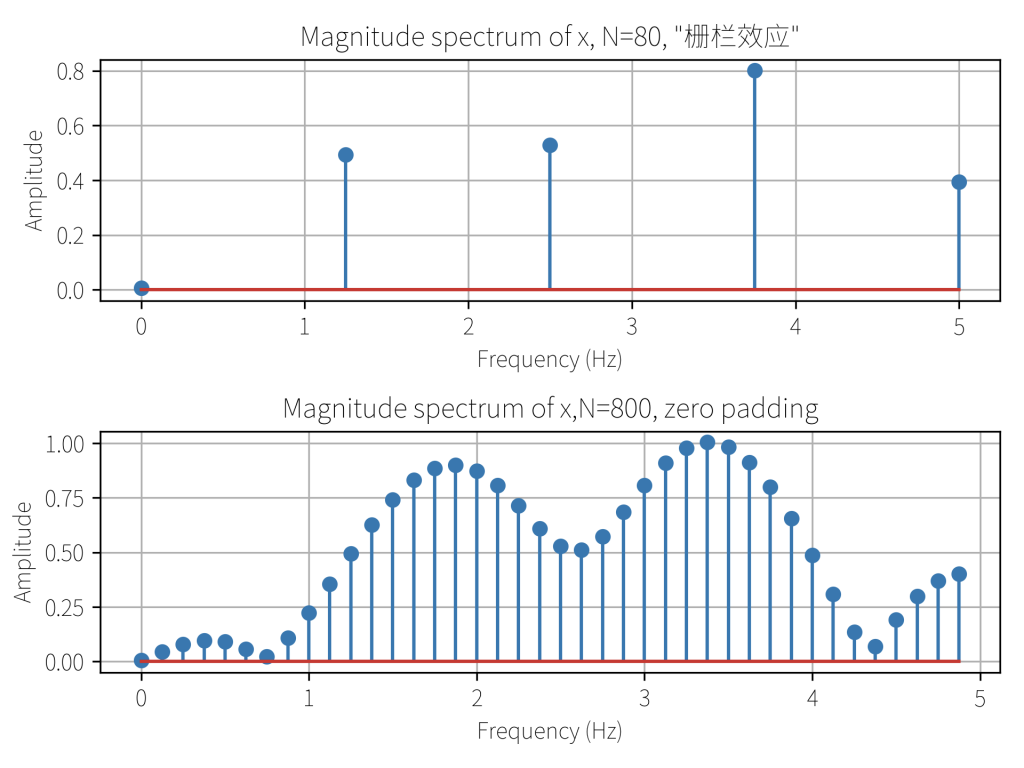
运行结果:
我们只能通过有限个点来观察离散傅里叶变换得到的频谱图,就像透过栅栏观察(频率数值点)一样。像上图中N=80那样,如果取样点过少,栅栏效应就会很严重,f1=2 Hz和f2=3 Hz “就好像被栅栏的板条遮住一样”,我们透过栅栏的缝隙只能观察到f=1.25, f=2.5 ... 的离散频率点。