This post was published in 2022-03-29. Obviously, expired content is less useful to users if it has already pasted its expiration date.
这篇文章是3月底写的,但是没搞定,留了一地垃圾。先放出来,6月份开始逐步修改没写的内容
Table of Contents
后续补充
本文涉及到了chord recognition,对这个流程现在有了更清晰的认知,见:🔗 [Chord recognition - Truxton's blog] https://truxton2blog.com/chord-recognition/
本文对音乐识别领域的部分难度认知有偏差。
主要内容
HMM模型在音乐识别领域的知识
前两天学习的是general HMM model:🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/
主要参考资料
《fundamentals of music ....》
TODO
envelop,ADSR model,顺便补充一下以前写的aspma
术语中英文对照
Timbre,音色
"Timbre allows a listener to distinguish the mu- sical tone of a violin, an oboe, or a trumpet even if the tone is played at the same pitch and with the same loudness." (《fundamentals of...》 P26)
ADSR model/ADSR envelop
以下内容来自《fundamentals of...》 P27开始
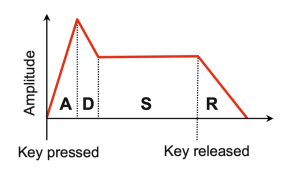
A: attack
D: decay
S: sustain
R: release
补充1:sustain并不一定要是严格的水平线,它可以是一个轻微衰减的曲线。
补充2:attack和release是一定会有的,而decay和sustain对有些乐器而言并不存在。具体补充内容见:🔗 [合成器基础:ADSR包络线 - 知乎] https://zhuanlan.zhihu.com/p/81771109
补充3:有关sustain跳转到attack的情况,见这篇笔记的PDF第2页:🔗 [论文阅读:《Real-Time Audio-to-Score Alignment of Music Performances Containing Errors and Arbitrary Repeats and Skips》 - Truxton's blog] https://truxton2blog.com/paper_reading_real_time_audio-to-score_alignment_of_music_performances_containing_errors_and_arbitrary_repeats_and_skips/,简而言之就是,(举一个例子)使用钢琴踏板保持sustain的状态(但手指已经抬起),然后手指重新按下去对应attack,所以就是sustain->attack.
temporal
这并不是什么音乐领域的专业术语词汇:“和时间相关的;时间的”
Music is typically organized into temporal units, referred to as beats.
《the fundamentals ...》P32
有待补充的内容
measured notes, grace note
artic
单音符泛音和三和弦的频谱问题
三和弦
先学习:12 major triads + 12 minor triads,除此之外当然还有其他triads,但这里暂时不讨论 .
除去严谨的枚举定义,要想快速理解也是非常容易的:中国业余钢琴考级的基本练习,9级和10级:(6*2)+(6*2)=24
所以只要演奏不错音,绝大部分场合都可以用识别出来的feature vector直接匹配24个预先准备好的三和弦的模型,从而识别和弦!
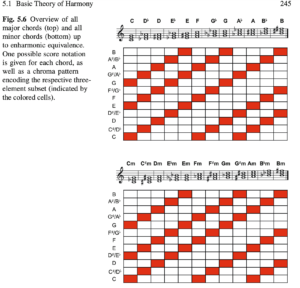
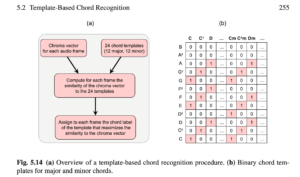

相似度判别方法包括欧式距离、余弦距离(等)。
单音符的频谱图
首先复习了一遍sinusoidal model和harmonic model,并补充了一些笔记:🔗 [ASPMA课程大纲复习(2021-06初版) - Truxton's blog] https://truxton2blog.com/aspma-syllabus-review/
第一个问题:弦乐器演奏单个音符的音频,是否属于harmonic model?
属于!下面的频谱图来自真实小提琴(而不是midi键盘合成小提琴声音)演奏的A4:
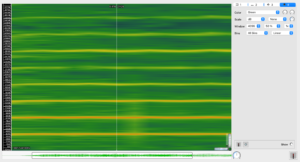
可以看到,能量峰值非常接近:440, 880, 1320, 1760 ...(Hz),都是整数倍,符合harmonic model .
为什么会有这样的结果?见:🔗 [2021-12-31 - Truxton's blog] https://truxton2blog.com/2021-12-31/
此外,这种现象(指乐器的harmonic series)会对chord recognition的准确性造成影响。(见《fundamental...》p261)
三和弦的频率叠加问题
十二平均律、频率、弦的物理振动,这些内容都有一定的联系。那么三和弦的产生是否也和频率有关联?
首先是一个非常生物学的回答:为什么大三和弦使人类有愉悦感? - 海阳的回答 - 知乎 https://www.zhihu.com/question/455070995/answer/1840037649
也可以参考这个回答:🔗 [不协和音程使人感到不和谐的原理是什么? - 知乎] https://www.zhihu.com/question/20010040
然后是为什么小二度非常难听的笔记:🔗 [论文阅读:《Real-Time Audio-to-Score Alignment of Music Performances Containing Errors and Arbitrary Repeats and Skips》 - Truxton's blog] https://truxton2blog.com/paper_reading_real_time_audio-to-score_alignment_of_music_performances_containing_errors_and_arbitrary_repeats_and_skips/#零碎知识

所以结论就是:

如何量化叠加频谱的“稳定、整齐”?🔗 [Plomp_Levelt_Tonal_1965.pdf] https://www.mpi.nl/world/materials/publications/levelt/Plomp_Levelt_Tonal_1965.pdf
三和弦的推导
我无法确定下面列举的方法是正确的,因为我还没有在任何一本正规书籍或大型教学网站上发现它。
并且:先计算整数倍频率再筛选的方法看起来非常滑稽,有的地方逻辑无法自洽(都用上major third, minor third和perfect five了为什么还要先计算频率啊?那干嘛不直接套perfect five?)
注意这里讨论的是 triads ,更具体化的chord.
现在已经知道了harmonic series,也知道了三和弦频谱叠加的规律,那么:给定一个C,如何用整数倍频率(harmonic series)推导出C major: C E G呢?
先计算整数倍频率,再筛选
首先使用harmonic series进行整数频率乘法计算:
(注:下面这张表偷懒了,直接从C4开始算)

然后牢记下面这个major triad的原则:
The interval between the root note and the second note is a major third, and the interval between the second note and the third note is a minor third ... the interval between the root note and the third note is a perfect fifth.
《Fundamentals of …》P243
那么什么是major third,什么是minor third呢?
查表!

所以现在放出前面那张推导了一半的图的完整版:
(注:下面这张表偷懒了,直接从C4开始算)
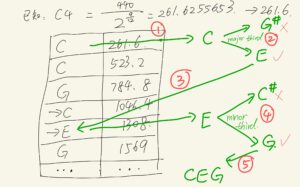
所以现在我们得到了C E G,其中C和E之间是major third,E和G之间是minor third!
现在开始推导minor triad,比如f小调:
root和second note之间是minor third,second note和third note之间是major third;同样,root和third note之间是perfect fifth.
但是会遇到一点问题,比如:

看起来不是很妙,查表都快查完了,为什么我还没有遇到[mathjax]A^b[/mathjax]?
这是因为root的频率选得太高了。之前计算major triad没有遇到类似的问题可能是因为运气。
如果还要用这种方法计算f minor triad,需要从F(0)=21.83开始计算,直到发现[mathjax]\mathbf{A}^{b}(5)[/mathjax]=830.6,而830.6/21.83=38.048557,确实是整数倍。
另一种方法:用major/minor triad的定义推导note,再验证频率
这个方法就是各大乐理书中常见的方法,只是在这里多加了最后一步:验证频率是否满足harmonic series的整数倍关系。
本文的前置知识
前置条件:在此之前,我们假定我们已经可以做到“seperate chroma”的识别:
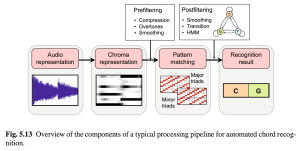
看书范围
由于之前的内容(HMM的3个基本问题)已经学过了,所以从5.3.4开始看
HMM模型的细致程度
2022-07-21更新:在《Fundamentals of …》chord recognition一章里,使用的HMM模型为discrete HMM model,但作者提到了“基于PDF的连续概率模型效果应该更好”的观点。
考虑以下3种场景的异同:(尤其是考虑使用GMM还是discrete model)
场景1:训练、识别声音0~9
场景2:训练、识别major C和弦
场景3:训练、识别一系列和弦,主要研究和弦之间的跳转问题
| 盒子抽球的HMM模型 | 和弦识别模型 | |
| 状态 | 盒子 | 12 major triads + 12 minor triads(见表格后的公式) |
| “隐藏“ | 盒子是隐藏的, 我们不知道抽出来的球到底来自哪个盒子 | 真正的和弦是隐藏的, 人耳只能听到演奏和弦带来的音频信号 |
| emission | 抽出的是(离散的)球, 我们一般会给盒子抽球HMM模型建立一个离散的emission probability model. | 虽然和弦是固定的,但演奏和弦带来的音频信号不是固定的,会存在快慢、频率差异等变化。 所以会有2种建模方式: 1. 我们给观测到的音频信号强行做一个quantization,分类完毕以后再输入到模型里,这样就可以大大简化这个模型(又称discrete HMM model)。这种模型可以考虑用Viterbi training,因为模型简单 2. 用GMM建模,执行常规的、使用soft EM算法的HMM-GMM模型。 |
附:和弦识别模型的状态:
[mathjax-d]\mathcal{A}=\left(\alpha_{1}, \ldots, \alpha_{I}\right):=\left\{\mathbf{C}, \mathbf{C}^{\sharp}, \ldots, \mathbf{B}, \mathbf{C m}, \mathbf{C}^{\sharp} \mathbf{m}, \ldots, \mathbf{B m}\right\}[/mathjax-d]为什么音乐音频分析仍然具有难度
(划掉)ASR:即使是同一个人说同一个字/同一句话,音频信号仍然有相当大的区别,所以ASR比较难;音乐音频分析:呃,以钢琴为例,一共就那些键,还遵循12平均律,那理论上来说对频域信号的分析应该相对简单一些才对。为什么还能见到很多HMM识别音符的论文呢?(划掉)
更新:这个说法有点问题,见:preview 🔗 [2022-07-19 - Truxton's blog] https://truxton2blog.com/2022-07-19/#对错误识别的容忍程度
后验概率/Posterior probability
🔗 [后验概率 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/后验概率
串联多个HMM模型
现在的模型适用的范围被扩大了,可以看作是“对每一个 Note/音节 视作一个HMM模型,然后把这些HMM模型依照一定限制串起来”。这个问题在ASR领域是language model的一部分,但是我们现在先从最简单的模型开始学习。
配套的NTU公开课:[單元 8.第八章 Search Algorithms for Speech Recognition]
DTW
补充:因为遗忘,后面又复习了一遍,进行了一些补充:🔗 [2022-07-21 - Truxton's blog] https://truxton2blog.com/2022-07-21/#ASR和MIR的DTW应用场景与建模方法
防止走失,台大公开课提到DTW的地方:🔗 [數位語音處理概論 - 臺大開放式課程 (NTU OpenCourseWare)] http://ocw.aca.ntu.edu.tw/ntu-ocw/ocw/cou/104S204/8
除了NTU公开课,还可以复习以前写过的DTW程序:🔗 [Audio Thumbnailing - Truxton's blog] https://truxton2blog.com/2020-12-15-audio-thumbnailing/
DTW是HMM开始流行之前的ASR方法。
场景举例(*来自NTU公开课):现在要辨别一个单词"thumbnailing",可以先收集很多"thumbnailing"发音的音频(p.s. 这里暂时假定这些音频都是同一个人发出来的,因为这样的场景比较简单),它们的长短各不相同。我们从中间挑选出一个长度比较合适的,然后以它为基准,对剩下所有的音频进行DTW配对,通过调整DTW参数从而做到全局较为良好的匹配。接下来任何新加进来的音频都会与这个模型进行匹配,计算相似度,从而达到语音识别的目的。
补充:加上下面2张图一起理解效果更佳,要注意理解DTW坐标轴上的数字到底代表ASR的哪一个抽象层(是MFCC,还是triphone,还是识别出来的单个字,还是...?):
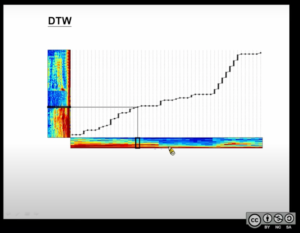

DTW参数:DTW模型的参数和HMM-Viterbi模型的参数略为不同,主要体现在部分“走法”的距离计算上:
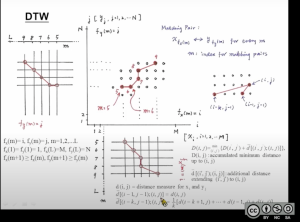
优势场景:儿童玩具,用于识别简单的、固定的读音,比如"hello/goodbye"这种。由于儿童玩具使用的硬件资源非常有限,所以只能做到这些。
Viterbi回溯查找
又发现了知识点记不牢固的问题,赶紧记下来,见:🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/#Viterbi_algorithm和Forward_algorithm的对比
从[單元 8.第八章 Search Algorithms for Speech Recognition]38分左右开始
先来一个简单的例子:发音0~9,反复说
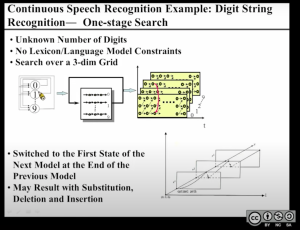
其实就是堆叠/排布一系列HMM模型,对每一个模型使用Viterbi算法,每当一个HMM模型使用的Viterbi算法走完了以后就马上跳转到下一个HMM模型的开头。
计算出预测序列以后再使用DTW和正确答案进行匹配:
(注意:此处建议先联动🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/#有关HMM自旋等结构的思考)

然后是现实场景中真正的例子,要复杂很多
(这里先跳过)
Viterbi back-tracking与”重复阅读练习“
(鸽了)
OCR辅助查找工具
epny|du 5 AD S R Key pressed Key released Prefiltering Postfiltering Compression Smoothing Overtones Transition Smoothing HMM Audio Chroma Pattern Recognition representation representation matching result Major triads C Minor triads Fig. 5.13 Overview of the components of a typical processing pipeline for automated chord recog- nition. DTW C3;. 191, 2, -NI N f y lm)= j Matching Pair ^ tylm) ** 3 ty lim) fw every m m m : index for malthing pates C-1, j-1) M: 5 f, Cm) = i (8-k. j-1) 1y (m)2 j M [%: . 191,2,- M] f,(m)= i, f,(m) = j, m=1,2,..L £, (1) = f,(1)= 1, f,(L) -M, f, (L) = N D(i,j)=, 5, (D(1, 5 ) + d101, J): (1, 5)]), f,(m+1) ≥ f(m), f,(m+1) ≥ f,(m) 5, (m) = i D(i, j) : accumulated minimum distance up to (i, j) d [Mi’, j); (1, j)] : additional distance extending (1’, j’) to (i, j) d (i, j) = distance measure for x, and y d[(i - 1, j - 1); (i, 0)] = d(i, j) m d[(i - k, J - 1): (1, j$ -[d(i- k +1, J) + .. + d(i-1, A ad BY NC SA Continuous Speech Recognition Example: Digit String Recognition- One-stage Search Unknown Number of Digits No Lexicon/Language Model Constraints Search over a 3-dim Grid 00,0; Switched to the First State of the Next Model at the End of the Previous Model May Result with Substitution, optimal poth Deletion and Insertion BY NC SA Recognition Errors Reference: 67341163 208 (T) \ 11 \ Aligned Recognized: 570814014 insertion deletion substitution (I) (D) (S) T-D-S-1 X100 T 100% = Accuracy BY NC SA