This post was published in 2022-03-20. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
写在最前面
这篇笔记不知不觉变成了一个肥胖臃肿的巨无霸,各种更新、纠正、补充都想往里面塞。但即使如此,还是尽量不要大改这篇文章的内容,有不满意或补充的内容可以另开一篇笔记,但错误的内容还是要改的:本篇笔记经历了若干次大改,为了保持逻辑自洽而增删了很多内容。
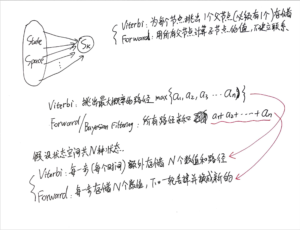
两种Forward Algorithm以及它们的转换
最开始,在跟随NTU公开课记录了这篇笔记的时候,forward-backward algorithm的表达公式和李航《统计学习方法》一致:


这个Forward/Backward algorithm被用来计算likelihood(单独的forward或单独的backward,以及两者的结合都可以),forward-backward algorithm用来构建EM算法。
很多时候大家都喜欢直接用forward-backward algorithm,而不是单独的forward algorithm;所以如果看到forward-backward,那么基本上就是上面这个算法。
但是在2022-07~2022-08,在学习Bayes net和bayesian filtering以后,又学到了另一种类型的forward algorithm(主要来自一个CMU的slide):
定义[mathjax]P(S_t \mid O_{1:t}, \lambda)[/mathjax]为forward algorithm,这个表达式其实是个bayesian filtering.
如果要做bayesian smoothing,那就要加上一个 看起来拥有backward精神 的"backward" algorithm:
preview 🔗 [贝叶斯网络 - Truxton's blog] https://truxton2blog.com/bayesian-network-introduce/#HMM_variable_elimination(Forward-Backward算法的推导原型)
在极少数教学资源里,推导bayesian smoothing的算法也会被称为forward-backward algorithm.(比如上面笔记里CMU slide),但很少很少,我就见过CMU slide那一个例子。
wikipedia怎么说?
在wikipedia里面,Forward algorithm被认为是bayesian filtering,而(另一种,不是bayesian filtering的)Forward/Backward algorithm被用来计算likelihood,forward-backward algorithm用来构建EM算法。(和李航、NTU等绝大多数网络资源一致)
本篇笔记怎么说?
本篇笔记毕竟是一篇Garbage笔记,不希望做太多的改动,以最开始的版本(Forward-backward algorithm被用来计算likelihood和EM算法)一致,且默认forward algorithm不是bayesian filtering.
事实上,这2种Forward algorithm的表达式是可以相互转换的:
forward-backward中的forward:[mathjax]\text{(Forward-Backward)}\alpha_t(i)=P(O_{1:t}, S_t=i \mid \lambda)[/mathjax];
bayesian filtering,单独的forward:[mathjax]\text{(Bayesian-Filtering)}\alpha_t(i)=P(S_t=i \mid O_{1:t}, \lambda)[/mathjax].
转换:
[mathjax-d]\text{(Bayesian-Filtering)}\alpha_t(i)=\frac{\text{(Forward-Backward)}\alpha_t(i)}{\sum_{S_t}\text{(Forward-Backward)}\alpha_t(i)}[/mathjax-d]在本笔记后面也会提到这方面的内容。
今天的主要内容
更系统地学习ASR,主要参考课程:🔗 [數位語音處理概論 - 臺大開放式課程 (NTU OpenCourseWare)] http://ocw.aca.ntu.edu.tw/ntu-ocw/ocw/cou/104S204/1
本篇文章主要记录以下章节的学习内容:#1, #2, #3(#3没有视频,因为只有10分钟,所以在#2视频的末尾),#4
本文的绝大部分截图和PDF都来自NTU课程,遵循🔗 [Creative Commons — 姓名標示-非商業性-相同方式分享 3.0 台灣 — CC BY-NC-SA 3.0 TW] https://creativecommons.org/licenses/by-nc-sa/3.0/tw/
联合概率和条件概率 *
上一次提到:🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
(李航统计学习方法p197)[mathjax]P(O, I \mid \lambda)=P(O \mid I, \lambda) P(I \mid \lambda)[/mathjax]
🔗 [probability - Why is P(A,B|C)/P(B|C) = P(A|B,C)? - Cross Validated] https://stats.stackexchange.com/questions/258379/why-is-pa-bc-pbc-pab-c
用“0~9声音识别”的场景来套用3个HMM基本问题
一张老图:

现在重新审视整个ASR项目,用“一个人发0~9的音”的场景来套用这3个HMM基本问题:
现在有10组训练数据,第一组训练数据收集了1000个人说“0”的声音,第二组数据收集了1000个人说“1”的声音,...;用这10组数据分别训练10个模型:
训练的时候,(对每个训练模型而言)是“学习问题”(尽管实际情况要比这个复杂一些):我们要训练出每个发音对应的模型[mathjax](A, B, \pi) [/mathjax] . 大部分情况下这个过程中需要用到forward-backward algorithm.
HMM模型可能只有3或5个状态,但是要“产生”很多observations,所以必定会存在“自身跳转到自身”的情况。给定observations,要找出对应的state状态,这是“解码问题”。大部分情况下这个过程中需要用到Viterti algorithm.
训练完10个模型以后,再找一个发音丢到这10个模型里去分别计算(用来寻找匹配度最高的模型),这是“概率计算问题”。大部分情况下这个过程中需要用到forward-backward algorithm.
有关HMM“自旋”等结构的思考
这一节是补充内容,放在forward/backward等算法之前,方便更好地理解HMM项目的应用。
如下图所示,很多时候我们会看到各种各样的HMM结构图,这些结构图都有什么区别呢?
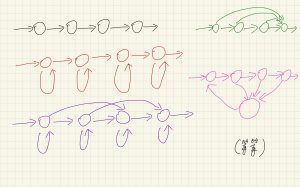
首先来思考一个奇怪的问题:在盒子抽球模型里,如果幕后抽球的人「抽到第2个红球以后,下一步一定会转向第#2个盒子开始抽球,然后遵循正常转移规律抽好几次」,那这样的情形还能被HMM模型较好地抽象出来吗?
是不可以的。要注意到HMM模型[mathjax](A,B,\pi)[/mathjax]本身承载的信息量有限,无法精准地压缩出上面的信息。
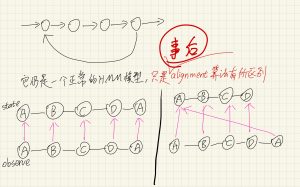
在这种情况下:HMM模型的建立、训练、测试都没有任何变化,有变化的只是「拿到观测数据以后和原始数据进行对比」。
为什么说“HMM的训练没有变化”?它应该如何训练?
⚠️注意一个容易搞混的地方:
在《Real-Time Audio-to-Score Alignment of Music Performances Containing Errors and Arbitrary Repeats and Skips》论文中,有这样的空间估计:

乍一看,空间复杂度为[mathjax]\mathcal{O}(4(N-1))[/mathjax],是不是说明[mathjax](A,B,\pi)[/mathjax]有变化呢?不是的,仔细阅读原文括号中的注释可知,多占用的空间并没有分给[mathjax]A[/mathjax],而是分给了HMM模型以外的超参数。
对比两个简单HMM模型(盒子抽球,语音识别)
对比“(这是一个pdf文件的链接)盒子和球的模型(可以简化这个模型里的跳转概率)”与“简单的语音识别模型”:
| 盒子和球的模型 | 简单的语音识别模型 | |
| 3种颜色的球 | 很多基本的发音单位 | |
| 3个盒子,隐藏了编号 | 3个或5个隐藏的状态,我们无法直接得知状态,因为我们用人耳只能“听” | |
| 不可观测的state | 盒子的编号 | 由一个phoneme或者一个tri-phone拆分出来的3个/5个状态 |
| 由state产生的observation | 从(不知道哪一个,也就是随机)盒子里随机抽球 (所以是两个随机) | “状态“并不是音频信号,我们只能听到产生的音频特征向量(MFCC),不能听到“状态”; 由于“状态”之间会跳转(或者自跳转),跳转基于概率(随机),所以我们也不知道目前到底是哪一个状态; 即使是同一个state(比如英文字母'c')也会产生不同的发音(比如Car和Chevrolet),再加上人耳对发音频率有一定浮动的容忍度(音调高点低点都能认出来),所以可以简化为:从一个GMM模型里随机抽一种读音读出来。 |
| 两层随机 | 从(不知道哪一个,也就是随机)盒子里随机抽球 (所以是两个随机) | 所以有两层随机: 1,状态的跳转是随机的(当然也有一定限制,有些状态序列出现的概率非常非常低) 2,状态产生的音频信号是随机的(我们可以想象它根据某个指定的GMM模型产生) |
| “突破口“ | EM | EM |
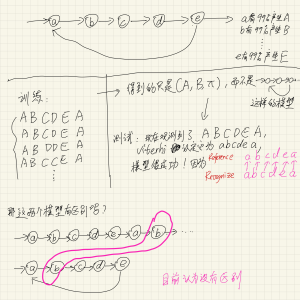
Likelihood问题:常规暴力算法
尽管这个算法几乎没有任何使用场景,但仍然要学一下:通过了解这个算法,能够更好地带入ASR使用场景,更容易理解“为什么这个模块要这样优化”。
首先我们有一个用烂了的公式:
[mathjax-d]\begin{split} S* & =\underset{S}{argmax}P(S|O) \\ & = \underset{S}{argmax} \frac{P(O|S)P(S)}{P(O)} \\ & = \underset{S}{argmax} P(O|S)P(S) \end{split}[/mathjax-d]现在观察这个公式,解释如下:已知观测序列[mathjax]O[/mathjax],我想求最有可能的状态序列,但我不知道怎么求,所以我把这个公式拆成了两部分:[mathjax]P(S)[/mathjax]和[mathjax]P(O|S)[/mathjax] . 乍一看这两部分还是不好求,但我们可以通过暴力枚举的方法,列举所有可能的[mathjax]S[/mathjax],然后对其中的每一种[mathjax]S[/mathjax],都求一次[mathjax]P(O|S)P(S)[/mathjax],最后我们把所有枚举情况中的最佳结果找出来就可以。

HMM和Posterior probability的联系
下面这张图的前半部分来自:🔗 [后验概率 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/后验概率
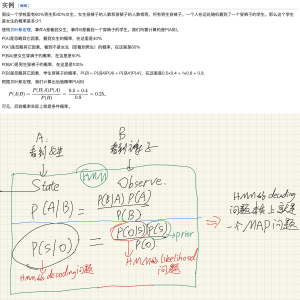
上面这张图最后的结论也可以参考这个wikipedia:
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models (HMM).
https://en.wikipedia.org/wiki/Viterbi_algorithm
Forward algorithm
再次注意本笔记开头部分的双重概念提醒:preview .
要解决的问题
Forward algorithm要解决的是什么问题/要求出什么东西?要解决的是Likelihood问题/概率计算问题,也就是求[mathjax]P(O|\lambda)[/mathjax]. 需要注意的是,单独拉一个forward algorithm出来就可以解决likelihood问题!
参考资料:NTU公开课或者李航统计学习方法p198-p199
* 还可以解决的问题:搜索问题
注意:下面这段文字是2022-08-02写的,原计划是用来反驳2022-03-20的笔记,但我在2022-08-23复习的时候不太同意我当时写的东西
* 这段话是2022-08-02写的;原来写的东西有点问题,暂时先折叠起来。
* 即使是新写的文字,我仍然觉得大有问题:主要是这段东西我没找到什么可靠的reference,当初貌似是自己空想出来的一个理想场景。
假设现在有一段很长的乐谱和一个已经建好的HMM模型(用整个note来作为时间单位,而不是time frame),我也知道整个乐谱的note序列。现在我听到了这段乐谱其中的一小部分:从note NO.0开始,我一直听到了note NO.T,但我并不知道我真正听到的是什么序列,更不知道这段序列在乐谱的什么位置。现在我需要猜测听到的这一段音频信号到底在乐谱的什么位置。
首先,这个算法不是Viterbi,因为我们不回溯!我们从note NO.0开始,每次听到一个新的note,就进行一次forward algorithm的计算,并且绝对不会在听完所有note以后回溯判断整个序列。
note 0:我们听到了note 0,我们使用forward algorithm对每个State(真正的note)都赋一个概率;
note 1:我们听到了note 1和note 0,我们使用forward algorithm对每个State(真正的note)都赋一个概率,这个计算是在note 0的基础上继续进行的;
note 2:我们听到了note 0,note 1和note 2,我们使用forward algorithm对每个State(真正的note)都赋一个概率,这个计算是在note 1的基础上继续进行的;
.....
note T:我们听到了note 0,note 1,note 2,... note T,我们使用forward algorithm对每个State(真正的note)都赋一个概率,这个计算是在note (T-1)的基础上继续进行的;
结束了。在理想情况下(HMM建模比较准确,且不错音),当我观测到note 0~note T的某个note x时,我应该会得到一个比较“有信心”的信念分布,就像一个很瘦的Gaussian model ,现在我就可以大胆推测:note x的实际状态应该是:???,因为我得到了一个很有信心的概率分布。如果不错音的话,下一个note (x+1)我也应该很有信心,以此类推...在note x之后的所有note我都应该很有信心才对。
这样就能够在乐谱上找出这段音频信号所在的位置了(当然,搜索的方法也很多样化)。
但是得到了这个结果似乎也没有什么用,因为...太理想化了,稍微出点问题就嗝屁。相比于viterbi,唯一有好处的地方在于:大大节省了空间,理想情况下根本不需要存储过去判断出来的note和state,只需要「Forward递推->大胆判定->继续Forward->丢掉所有用过的数据->...即可」。
注意:下面这段文字是2022-03-20前后写的,但我在2022-08-02复习的时候不太同意我当时写的东西
假设现在有一段乐谱记为「EDCDEEEDDDEEE」,对这段乐谱使用HMM建模(每一个note代表一个状态),然后我听到了一段音乐:这段音乐实际上计划发出「CDEEED」的声音,但目前我只听到了「CDE」,现在我需要找出当前听到的「CDE」位于乐谱的什么位置。
一个非常暴力的方法如下:
比较「EDC」和「CDE」,使用Forward algorithm计算概率(注意:这里可以使用Forward algorithm,因为并没有听到完整的序列);
比较「DCD」和「CDE」,使用Forward algorithm计算概率;
比较「CDE」和「CDE」,使用Forward algorithm计算概率;
比较「DEE」和「CDE」,使用Forward algorithm计算概率;
...
有点类似于substring搜索算法,这里使用的是原始的暴力匹配算法。当然实际识别乐谱不会像这样简单,这里只是举一个非常理想的例子。
完整公式

推导
(参考了徐亦达老师 https://www.bilibili.com/video/BV1BW411P7gV?p=4)


笔记1
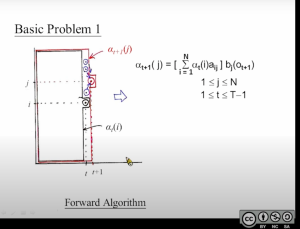
对前向概率[mathjax]\alpha_{t}(i)[/mathjax]的解释:
注:本文同时拥有2种表述「状态」的数学符号:[mathjax]q[/mathjax]和[mathjax]s[/mathjax].
[mathjax-d]\alpha_{t}(i)=P\left(o_{1}, o_{2}, \cdots, o_{t}, q_t=i \mid \lambda\right)[/mathjax-d]我从时刻[mathjax]1[/mathjax]开始观察,一直观察到时刻[mathjax]t[/mathjax]。在时刻[mathjax]t[/mathjax]的时候,我已经观察到了这些状态:[mathjax]o_1, o_2, o_3, … , o_t[/mathjax],且我对时刻[mathjax]t[/mathjax]真实状态的概率分布情况有了清楚认知。那么我(在时刻[mathjax]t[/mathjax]的时候)实际观测到[mathjax]o_1, o_2, o_3, … , o_t[/mathjax]的几率是多少?[mathjax]\sum_{i=1}^{N} \alpha_{t}(i)[/mathjax] .
等等,上面所述的「几率」到底是什么几率?事实上在学习forward algorithm的过程中我不止一次犯了愚蠢的认知错误。我们要求的概率是[mathjax]P\left(O_{1:t}, q_t=i \mid \lambda\right)[/mathjax],而不是[mathjax]P(O_{1:t} \mid O_{1:T})[/mathjax]!
在forward algorithm递推到最后一个时间[mathjax]T[/mathjax]的时候,终于可以求出[mathjax]P(O \mid \lambda)[/mathjax]了:此时:
[mathjax-d]P(O \mid \lambda)=\sum_{i=1}^{N} \alpha_{T}(i)[/mathjax-d]笔记2
看起来非常类似Dynamic programming的一个子步骤:
可以把这张图看作是”一个竖着的扫描线,从左扫到右“
这个扫描线每向右移动一步,就更新这条线上的所有点;
如何更新?对于时间线[mathjax]t+1[/mathjax]扫描线上的任意一点[mathjax]j[/mathjax],都需要使用上一条扫描线上的所有点进行计算:由于上一条扫描线上的所有点都可以到达[mathjax](t+1,j)[/mathjax]这个点,所以需要统计跳转概率之和;
再观察这个公式:
[mathjax-d]\alpha_{t+1}(i)=\left[\sum_{j=1}^{N} \alpha_{t}(j) a_{j i}\right] b_{i}\left(o_{t+1}\right), \quad i=1,2, \cdots, N[/mathjax-d]为什么求和公式之后还需要乘上一个发射概率?每一步都乘上发射概率,最后会得到什么?注意这是一个递推公式,而HMM模型【每一步都需要统计出一个观测结果,而不是只统计最后一个观测结果】。
笔记3
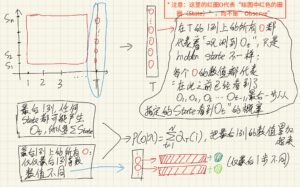
现在我执行了一遍forward algorithm,从第一列“扫描”到了最后一列,得到最后一列数值,接下来我应该怎么做?
应该把最后一列的数值累加起来,这样就能得到最终概率。
Backward algorithm
要解决的问题
单独拉一个Backward algorithm就可以解决likelihood问题;和forward algorithm结合可以解决:EM训练问题。
完整公式

结合Forward algorithm和Backward algorithm
总结公式
结合forward probability和backward probability可以用来计算:Bayesian filtering和Likelihood. 虽然单独的forward或backward也能解决likelihood问题,但它们需要递推计算到各自的终点(forward需要递推到t=T,backward需要递推到t=1)。

推导上面的公式推荐看徐亦达老师的slide:

接下来是NTU课程里的内容(上面的内容是2022-08-23补充的,下面的内容是2022-03-20跟随NTU课程一起记录的原始笔记)

蓝色:forward algorithm;红色:backward algorithm,注意forward algorithm “包含”目标计算点,而backward algorithm “不包含”目标计算点。

注意到上图的最后一行公式凭空出现的[mathjax]t[/mathjax]:
[mathjax-d]\mathrm{P}(\overline{\mathrm{O}} \mid \lambda)=\sum_{\mathrm{i}=1}^{\mathrm{N}} \mathrm{P}\left(\overline{\mathrm{O}}, \mathrm{q}_{\mathrm{t}}=\mathrm{i} \mid \lambda\right)=\sum_{\mathrm{i}=1}^{\mathrm{N}}\left[\alpha_{\mathrm{t}}(\mathrm{i}) \beta_{\mathrm{t}}(\mathrm{i})\right][/mathjax-d]由于[mathjax]\mathrm{P}(\overline{\mathrm{O}} \mid \lambda)[/mathjax]是固定的,这就意味着:无论[mathjax]t[/mathjax]如何变化,代入公式求出来的[mathjax]\mathrm{P}(\overline{\mathrm{O}} \mid \lambda)[/mathjax]结果都是一样的。
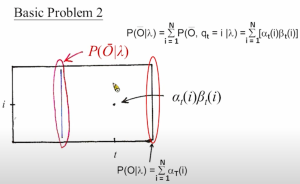
更直观地:在这张图上,对竖着的“扫描线”求和,无论“扫描线”的位置如何变动,都能求出一样的[mathjax]\mathrm{P}(\overline{\mathrm{O}} \mid \lambda)[/mathjax] .
现在单独分析某一条“扫描线”:这条扫描线上的任意一点,代表“我已经观测完整个序列,但我想知道在时间[mathjax]t[/mathjax]的时候,序列处于这个状态的几率是多少”。结果很显然,取这条扫描线上数值最大的点就会得到时刻[mathjax]t[/mathjax]最有可能处在的序列状态。事实上这就是下面所阐述的“Viterbi有缺陷的前置算法”的一部分:如果我们对每条扫描线,都求它们各自的“最有可能的状态”,那么把这些点连起来,看上去就求出了“已知观测序列,求最有可能的状态序列”的一种算法。
和单独Forward algorithm的本质区别
等等!好像有点迷糊,对“扫描线”任意一点的描述,怎么感觉和Forward Algorithm的描述长差不多,难道笔记记错了?再次重温Forward Algorithm的描述:
Forward Algorithm
我从时刻1开始观察,在时刻[mathjax]t[/mathjax],我已经观察到了这些状态:[mathjax]o_1, o_2, o_3, … , o_t[/mathjax] ;时刻[mathjax]t[/mathjax]的任何一个状态都有概率产生观察[mathjax]o_t[/mathjax],那么“已经观测到[mathjax]o_1, o_2, o_3, … , o_t[/mathjax],且时刻[mathjax]t[/mathjax]的状态是[mathjax]i[/mathjax]“的几率是多少?[mathjax]\alpha_{t}(i)[/mathjax] .
区别就在于:Forward + Backward algorithm的条件是“观察完所有的序列”,而Forward algorithm的条件仅仅是“观察到时刻[mathjax]t[/mathjax]为止(后面能观察到什么也不知道)”。
这篇博客里有一个例子:🔗 [从零学习Belief Propagation算法(三)_你通透就好 别问我是谁的博客-CSDN博客_belief propagation算法] https://blog.csdn.net/qq_23947237/article/details/78389188

对与这个队列中的任何士兵而言,想要知道整队人数,都必须经历一个“发射询问消息,等待询问消息到达队列末端并返回”这样一个完整流程。以最左边的士兵为例,他发送了一条询问消息以后,这条消息向右传递:传递路径上的任何士兵(最右边的士兵暂时排除)都不可能知道整队到底有多少人。
Viterbi的前置算法(有缺陷的算法,一般不用)
在Viterbi algorithm之前,还有一种(有缺陷,一般不会拿来用)简单算法,即:结合了forward和backward的算法:

(重复一遍之前的文字)* 现在单独分析某一条“扫描线”:这条扫描线上的任意一点,代表“我已经观测完整个序列,但我想知道在时间[mathjax]t[/mathjax]的时候,序列处于这个状态的几率是多少”。结果很显然,取这条扫描线上数值最大的点就会得到时刻[mathjax]t[/mathjax]最有可能处在的序列状态。事实上这就是下面所阐述的“Viterbi有缺陷的前置算法”的一部分:如果我们对每条扫描线,都求它们各自的“最有可能的状态”,那么把这些点连起来,看上去就求出了“已知观测序列,求最有可能的状态序列”的一种算法。*
Viterbi algorithm
要解决的问题
Decoding问题

学习问题 (Viterbi training)
Viterbi也可以拿来解决学习问题(称为Viterbi training/hard EM),这部分写在本文后面。
模型匹配问题(能达到和Likelihood相似的结果)
* 特别注明:这里的Forward algorithm计算的是Likelihood:[mathjax]P(O \mid \lambda)[/mathjax] .
(这个在后面有提到)实际使用场景
Viterbi和Forward algorithm看起来解决的问题完全不同(一个是Likelihood问题,一个是decoding问题),但实际使用场景中经常比较它们两个。
(这个场景出自于NTU公开课)如果我训练好了1~9发音的9个model,接下来我输入一个声音(实际上是7,但我们并不知道),要辨别这个声音最有可能属于哪个model。
Forward algorithm:我们把声音丢进model 1,询问“这个声音属于数字1的概率有多大”(Likelihood),同理丢进2~9;
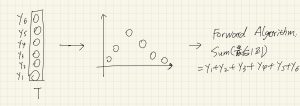
Viterbi:我们把声音丢进model1,询问“给我一个数值,这个数值越大表示这个声音越接近1”,同理丢进2~9;Viterbi要做的其实是 强行 让每个模型给出一条最接近自己的状态路径(以及这个“最优”状态路径的概率).
在绝大多数建模合理的实际应用场景里,Viterbi返回的数值已经足够用来判断模型匹配程度了,不需要用Forward algorithm计算“真正的概率”。见下图左下角:用Forward algorithm计算得到的“紫色、黄色、蓝色 ... 线段上所有点的累加”,而viterbi只会计算“紫色、蓝色、黄色 ... 的最高点”。可以很明显看出,由于紫色的位置过于“突出”,无论是用Forward algorithm还是用Viterbi,都会选出紫色作为最佳匹配模型,而Viterbi计算量明显低了很多,所以Viterbi就足够对付这种情况了。(Viterbi会翻车的案例暂时忽略不计)
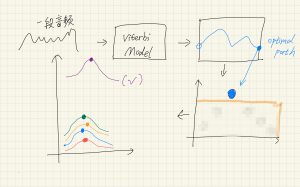
在下文还有1个关于Viterbi和Forward algorithm的例子。
为什么Viterbi可以累加局部最佳结果,从而代表全局最佳结果?
关于Viterbi路径选择的一个举例:
假设现在你正在玩一个类似巫师3这样的RPG游戏,你在某次任务中发现一个不起眼的山洞,顺着山洞一路走下去你意外地触发了一系列特殊的事件,你永远地留在了这个山洞中,游戏结束了,你得到了隐藏结局Z;反之,如果你不进这个山洞,那么你将会永远错过这个特殊事件,无论之后怎么玩都永远不可能走向隐藏结局Z了。
上面这个RPG任务模型就不能套用Viterbi。
另一个可以套用Viterbi的例子:
还是一个RPG游戏:你前往一个宫殿,打算去问4个问题,门口站了若干个卫兵。这些卫兵里面没有特殊NPC,不会特殊对话,他们也都知道你的4个问题的答案,你可以把他们看作几乎相同的NPC。现在你可以找其中1个卫兵询问4个问题,也可以用别的顺序问问题,反正一定要把4个问题问完。无论用什么方法问,最后得到的答案都是一样的。(当然这个例子并不是很严谨,只是肯定要比上面那个例子更适合Viterbi)
这个任务模型就可以套用Viterbi。得益于HMM模型的“无后效性”,一个state只会对接下来的state产生影响,不会对未来的state产生影响(类比于“一个公正的、不记仇的、没有累积惩罚机制的判决系统”)。
还是那个卫兵场景,假如现在修改这个场景:卫兵4有点精神疾病,连续问他3个问题会被他赶出宫殿,导致问题D问不出答案了。这种情况就不能用Viterbi。
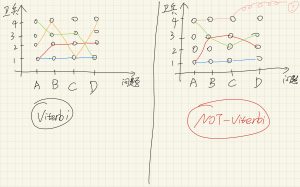
Viterbi和Forward Algorithm的对比(重复了)
其实下面的内容和前面的内容撞车了(下面的内容是前一天写的,前面的内容是后面新增的)
注:即使是重复内容,里面的观点我也并不认可:目前我认为在处理这类模型上,Viterbi和Forward algorithm的计算量应该差不多才对。
重复内容(有错误,不是很认可)

注意上面这张图,forward algorithm和viterbi之间并不是等价的。(在NTU公开课里可以找到类似的例子),用一个例子说明如下:
现在假设一个高中有50个班,这50个班里有一个班特别强大,平均水平远超其他49个班,现在你要通过一次考试成绩把这个班找出来。Forward algorithm的方法就是计算每个班的平均分,然后比较50个班的平均分;viterbi的方法是:让每个班分别拿出一个最高分,如果有一个班的最高分远超其他班,那么这个班大概率就是那个最强的班。当然这样做存在翻车的可能,即:
班1: 最高分100,其他的人平均分30
班2: 最高分90,其他的人平均分80
这样还是会翻车(只是存在理论上翻车的可能),但在现实场景里我们基本上见不到这样的例子,因为现实中基本上不会存在这样的班级分配(好学生肯定会被挖到好班里去,使得每个班的分数分布都近似于正态分布)。
Viterbi algorithm和Forward algorithm的对比
写完这篇文章过了几天又发现了新的问题,对Viterbi的掌握仍然不牢固,需要重新复习一些很容易搞混淆的内容。
”既然Viterbi算法非常高效,那么Viterbi的计算量应该要比forward的计算量小很多,对吗?“ 这个看法是错误的。虽然Viterbi和Forward解决的问题并不同,大多数场合下也比不到一块去,但如果硬要比较一下计算量也是可以的:Viterbi和Forward的时间复杂度应该是几乎一样的(目前认为计算机处理max(a1, a2, a3...an)的速度和计算(a1+a2+a3+...+an)的速度是一样的),而Viterbi还要额外占用空间来存放“最优候选路径”。
“我印象里Viterbi对每一步都可以用一个argmax这样的方法求局部最优,那么是不是Viterbi只需要像Forward algorithm那样从左往右扫描一遍,用一个数组把每一步的最优结果存起来,就可以结束了?“ 这个看法是错误的。首先,Viterbi algorithm一定会有一个"backtracking / 回溯",这是因为每一小步用argmax求得的结果只能代表“如果xxx,那么上一个时间最有可能”,而不能代表“它就是全局的最有可能”。换句话说,Viterbi的时间扫描线只有走到最后一步了才能正式确定最佳结果,然后才能开始回溯正确答案。
2022-08-23对Viterbi的补充笔记
做例题🔗 [2022-01-18 - Truxton's blog] https://truxton2blog.com/2022-01-18/ 的时候写的笔记。主要内容有:
再次复习Viterbi;对比Viterbi和Forward algorithm的不同(* 这里的Forward Algorithm是bayesian filtering版的forward algorithm)
笔记有点迷糊,先凑合用吧:



Baum-Welch Algorithm
现在面临一个全新的问题:学习问题。
什么是EM
首先我们要搞清楚"EM"在Baum-Welch中的含义:

假设我们一开始有一个很粗糙的model,我们要用一段声音去训练这个model:我们先把这段声音倒进去,学习到了新的model(具体学习方法见后面的内容)。但是这个更新后的model到底好不好呢?我们可以把更新后的model当作下一次学习的初始model,然后把同一段声音倒进去再训练一次,如此循环,直到这段声音再也不能对这个model产生任何显著改进。到了这时我们可以认为“这段声音真正融入了这个model,这个model真正学会了这段声音”。注意以上内容都是“同一段声音”的训练,这个model也只是“学会了”这一段声音,没有学会其他的声音。
更新跳转几率

公式中里红色标注的地方可以用下面2张图来理解:
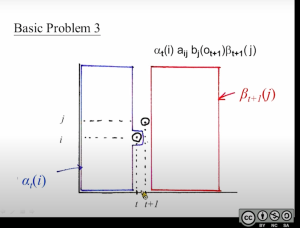
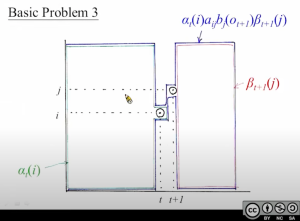
上面提到的两个公式,其中[mathjax]\gamma_t(i)[/mathjax]是先前已经学过的:在forward+backward的那一部分:观察完了整个序列,且要求时间[mathjax]t[/mathjax]的状态为[mathjax]i[/mathjax],其他时间的状态无所谓。
[mathjax-d]\gamma_{\mathrm{t}}(\mathrm{i})=\mathrm{P}\left(\mathrm{q}_{\mathrm{t}}=\mathrm{i} \mid \overline{\mathrm{O}}, \lambda\right)[/mathjax-d]新添加的概念[mathjax]\varepsilon_t(i,j)[/mathjax]可以理解为在[mathjax]\gamma_t(i)[/mathjax]的基础上进行了一些限制:不仅要在时刻[mathjax]t[/mathjax]的时候处于状态[mathjax]i[/mathjax],还要在时刻[mathjax]t+1[/mathjax]的时候处于状态[mathjax]j[/mathjax]. 有了这个限制似乎可以搞一个大胆的猜测:既然[mathjax]\varepsilon_t(i,j)[/mathjax]比[mathjax]\gamma_t(i)[/mathjax]更为“严格”,那么[mathjax]\frac{\varepsilon}{\gamma}[/mathjax]是不是可以粗略理解为“从状态[mathjax]i[/mathjax]跳转到下一个状态[mathjax]j[/mathjax]的概率”呢?
事实上是的:

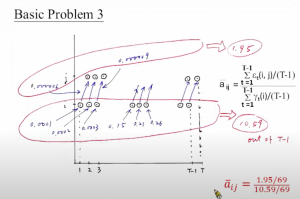
到目前为止的计算流程如下:
首先我搞一个初始化的模型[mathjax]\lambda[/mathjax],然后我用Forward algorithm求出[mathjax]\alpha[/mathjax],然后用Backward algorithm求出[mathjax]\beta[/mathjax],然后把[mathjax]\alpha[/mathjax]和[mathjax]\beta[/mathjax]拿过来结合初始化模型可以求[mathjax]{\gamma}[/mathjax]和[mathjax]\varepsilon[/mathjax]。最后我们算出了一个新的跳转几率,但我们还不知道怎么利用这个跳转几率做更多的事。
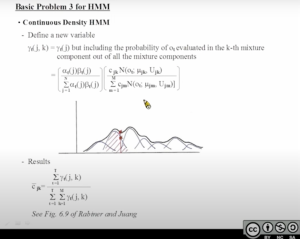
更新GMM模型的3个参数
现在已经搞定了[mathjax]\alpha[/mathjax](跳转几率)的更新,接下来还要处理“emission probability”的更新。这一部分涉及更新的变量有3个:mean, covariance, weight. (详细内容以后再补充)
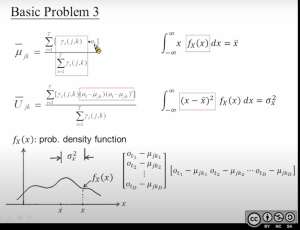

更新模型的初始状态
最后我们要更新HMM模型的初始值:[mathjax]\bar{\pi}_{\mathrm{i}}=\gamma_{1}(\mathrm{i})[/mathjax]
Baum-Welch Algorithm步骤概述
到目前为止我们的进度:
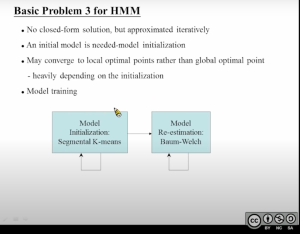
首先我搞一个初始化的模型[mathjax]\lambda[/mathjax],然后我用Forward algorithm求出[mathjax]\alpha[/mathjax],然后用Backward algorithm求出[mathjax]\beta[/mathjax],然后基于这两个结果更新了一系列HMM模型[mathjax](A,B,\pi)[/mathjax]的参数。接下来我们把新的模型参数代回原来的初始化模型,再做一遍Forward+Backward,再一次更新HMM模型[mathjax](A,B,\pi)[/mathjax]的参数 .... 直到迭代的模型几乎不再变化为止。现在遗留的一个问题在于:这个初始化的模型应该怎么搞?
HMM模型的初始化
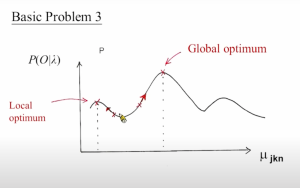
现在HMM Model Training的步骤可以描述为:先反复迭代segmented k-means得到一个初始化模型(初始化模型也是需要具有一定精确度的,具体原因见👇第2张图);然后把初始化模型送到Baum-Welch算法迭代中,得到更精细的模型。
重新理解Viterbi training (hard EM)和soft EM
模型初始化的segmented k-means放到后面再学习,先解决一个之前没完全懂的问题,然后结束本篇文章。
在此之前,Viterbi能够用来解决什么问题?Decoding问题。把观测序列塞到模型里去得到最有可能的路径。获得的这点信息也能用来更新模型参数吗?是可以的。(事实上,NTU的公开课里也提到了这个,只是把它称作“已经很落后的discrete HMM”)
在Baum-Welch算法里,我们使用GMM模型来套用emission probability;而更为“原始”的方法是,不使用Gaussian模型,我们直接计算每一个点的概率:(这个公式和GMM模型更新参数的公式很像)

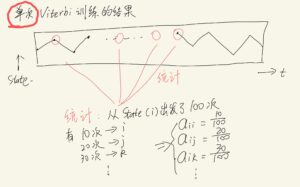
使用Viterbi进行训练的时候,每进行一次完整的Viterbi算法,都可以更新一次HMM模型。(2022-07更新:差点又误以为“把多次Vierbi的结果叠加在一起进行统计”,这是错误的!)(2022-08更新:把多次Viterbi的结果叠加在一起的做法也不是不行,但这样做已经很接近 有监督学习 了(见李航统计学习方法P203,或本笔记后面的内容),但它又不完全等于有监督学习,所以只能把它看作一个异类。)
GMM模型:用一些数据训练出GMM模型,但我们最后要利用的是“这个GMM模型生成的离散结果”。
Discrete HMM模型:用一些数据(往往需要很多)训练出一个离散模型(有点像是查表法/枚举法),训练完毕后这个模型发射的数据永远来自已经塞进去训练的数据。所以说这个模型高度依赖于训练塞进去的数据,而且占用空间很大。
更极端的例子:有监督学习
见李航统计学习方法P203
与之对应的是Baum-Welch:无监督学习。
有一点像“多个Viterbi结果的叠加(必须是不同观测数据得到的不同Viterbi path,否则没有意义)”,但实际上并不是:有监督学习使用的数据是 已经人工标注好的数据 :


注意上面这张图的第3条,使用多个标注好的数据可以用来估计HMM初始模型[mathjax]\lambda[/mathjax].
NTU slide
(遵循🔗 [Creative Commons — 姓名標示-非商業性-相同方式分享 3.0 台灣 — CC BY-NC-SA 3.0 TW] https://creativecommons.org/licenses/by-nc-sa/3.0/tw/)
OCR辅助查找工具
隐马尔可夫模型由初始状态概率向量开、状态转移概率矩阵A和观测概率矩阵B决定。丌和A决定状态序列,B决定观测序列。因此,隐马尔可夫模型入可以用三元符号表示,即入= (A, B,T) (10.7) A, B,①称为隐马尔可夫模型的三要素。状态转移概率矩阵A与初始状态概率向量丌确定了隐藏的马尔可夫链,生成不可观测的状态序列。观测概率矩阵B确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。 10.1.3隐马尔可夫模型的3个基本问题隐马尔可夫模型有3个基本问题: (1)概率计算问题。给定模型入=(A,B,T)和观测序列◎=(ol,02,⋯,0T),计算在模型入下观测序列◎出现的概率P(OIA)。 10.2概率计算算法197 (2)学习问题。已知观测序列◎=(o1,02,⋯,07),估计模型入=(A,B,元)参数,使得在该模型下观测序列概率P(OIA)最大。即用极大似然估计的方法估计参数。 (3)预测问题,也称为解码(decoding)问题。已知模型入=(A,B,元)和观测序列◎=(ol,02,⋯,or),求对给定观测序列条件概率P(IIO)最大的状态序列I=(i,i2,…,)。即给定观测序列,求最有可能的对应的状态序列。给定模型入=(A,B,元)和观测序列◎=(o1,02,⋯,or),计算观测序列◎出现的概率P(OIN)。最直接的方法是按概率公式直接计算。通过列举所有可能的长度为T的状态序列1二(n,2,⋯,T),求各个状态序列【与观测序列O = (ol, 02, ,oT)的联合概率P(O,IIA),然后对所有可能的状态序列求和,得到P(OIA)。 Basic Problem 1 Q+0 1Z Ca(j) = [.Z,ci)an J b(om) i=1 j 1≤j≤N 1 ≤t≤ T-1 - @,( 1 1+1 Forward Algorithm 000 BY NC SA首先定义前向概率。定义10.2(前向概率)给定隐马尔可夫模型入,定义到时刻七部分观测序列为o1,02,⋯,06且状态为Q:的概率为前向概率,记作 ar(i) = P(ol,o2,,0t,it = gal入) 可以递推地求得前向概率ot()及观测序列概率P(OIA)。 (10.14) 算法10.2(观测序列概率的前向算法)输入:隐马尔可夫模型入,观测序列◎;输出:观测序列概率P(OIN)。 (1)初值 a1()=不;bi(o1), {=1,2,⋯,N (2)递推对t=1,2,⋯,T-1, (10.15) 0t+1()= M or(i)aji b(ot+1), {=1,2,,N (10.16) (3)终止 N P(ON= 2ar() i=1 (10.17) S, S 200 ③9⑨O在下1到上站所有口都 2代表看现见洲到01”只是 (」专意现州到9%疑是hicen state不一样; 最台|列仁個每个D的教值都代花 Shate都可能多生‘在化之前己经看砂3 ,所以要三Siate 0.0,0-0-,最台-步从益台到上的新有排定的Stte為到l的顺室仅仅茶台[到字效級值不同Pen- So,G,把家么品表值路超果t=/ WIZZA+D {仅最后|步不司) DO⋯ -7zz2/z定义10.3(后向概率)给定隐马尔可夫模型入,定义在时刻t状态为q:的条件下,从t+1到工的部分观测序列为0141,0442,⋯.,07的概率为后向概率,记作 Br(a) = P(ot+1,0t+2,, or lit = gi,入) (10.18) 可以用递推的方法求得后向概率Be()及观测序列概率P(OIA)。算法10.3(观测序列概率的后向算法)输入:隐马尔可夫模型入,观测序列◎;输出:观测序列概率P(OIA)。 (1) 6r(i)=1, i=1,2,,N (10.19) (2)对t=工-1,公-2,.,1 NO- RoMlro.or {=1,2,,N (10.20) (3) Y P(OIA)= Znb(o)6®) (10.21) i=1 B.i). P(O, qt= i l) a(i) = Prob [observing 01, 02, Ot, …, o1, 9t=in] = OrO)p() Combining Forward/Backward Variables P(O, qt = i 2) Prob Tobserving 01,02; Or, or.qt=iln] oi)B(i) PON-g PO. 9-i2) -g Io.OB①] Basic Problem 2 ROn) 一PoM) -po. a=ih) -aOR N a,(DB(i) P(OI2)=2 QT(i) mMz i=1 Basic Problem 2 for HMM Approach 1 - Choosing state q.* individually as the most likely state at time t Define a new variable Y(i) = P(qt=i l 0, 2) Q①B ① Y①)=- P(O, qEin) 20⑥3① i=1 PON) Solution 9t= arg max V (il, 15 K≤T 15isN in fact 9t arg max KisN [P(O, qein) = arg max ISiSN [OOBOl Problem maximizing the probability at each time t individually q= quq2….qu may not be a valid sequence (e.g. agr. 0) ⑥③③ BY NC SA (3)预测问题,也称为解码(decoding)问题。已知模型入=(A,B,㓁)和观测序列◎=(ol,02,,0m),求对给定观测序列条件概率P(IO)最大的状态序列[三(i1,iz,…,i)。即给定观测序列,求最有可能的对应的状态序列。 16兴文大产OOOOO farvuond Algor/iehm Sum(泰台l3D Y =7+92+¥+/+¾+%一段音数1wn/l Vterbi Model optimek Perth (v)卫乐卫红, 4+ + S O 3 2 2 O ABCID问是A B Viterb (noT-Wrerb Basic Problem 2 for HMM Application Example of Viterbi Algorithm Isolated word recognition入. =(Ao.Bo.元,) A=(A,B,元) 2.=(A.,B.,元.) observation 0=(0,0…0) K’= arg max PIOl 2,J~ arg maxIP 12] 1sisn 1sisn Basic Problem Basic Problem 2 Forward Algorithm Viterbi Algorithm (for all paths) (for a single best path) -The model with the highest probability for the most probable path usually also has the highest probability for all possible paths. BY NC SA Iterative Procedure 入=(A, B,元)一元=(A,B.元) O= 0,02..0r It can be shown (by EM Theory (or EM Algorithm)) PO2≥PO2 after each iteration Basic Problem 3 Ye(i (D Be _ P(o.9t = il2) Za.OR.O] P(OIA) P(qt = il0, A) ct(i) ai b(Ot+1) Br+iG) &t(i,j= 2 (i) ay b (Ot+1) Pe+i() — P(O,qt L.Q=J- P(Qe = i,9c+1 = 10,7) P(OIA) Basic Problem 3 a(i)a,b(o+DB+/) -. B4ri a(i) t t+1 BY NC SA Basic Problem 3 0. rvoye 9 T-1 )OO 6. wwvo. N ® za(i, j)/(T-1)的-号DOo 00o o Z Y()/(T-1) t =1 0. ubol ^个公0. 15 0.2/ 0.26 0 vDt ’0.033 cwt o T-! T.I ai 1.95/69 10.59/69 Basic Problem 3 for HMM Continuous Density HMIM - Define a new variable YG.k=YG) but including the probability of or evaluated in the k-th mixture component out of all the mixture components GGBO) CAkN(OE HL U了n-1 NoRO J & Su Noe Wu. Uo) Results ZYG.k ,l z zrG,k) (-lkl See Fig. 6.9 of Rabiner and Juang Basic Problem 3 T Y,(j.k) H t=l L* f(x) dx =x ZY.0,k) (=1 T U, Zy,G.AKo,-4p(o—4A) (x• E) f(x) dx = G ZY,j.k) 1=1 fx(x): prob. density function好k -Ots -Hjki’ Ot2 Kjk2 x(x) or, Njki Ot,一Hjk2 Otp Mko LOtp一Rjkp. X x X BY NC SA ZyG, k C 1=1 M Z zM.k t-l kl See Fig. 6.9 of Rabiner and .Juang Basic Problem 3 for HMM • No closed-form solution, but approximated iteratively • An initial model is needed-model initialization May converge to local optimal points rather than global optimal point heavily depending on the initialization Model training Model Model Initialization: Re-estimation: Segmental K-means Baum-Welch BY NC SA Basic Problem 3 P Global optimum POIZ Local optimum Hjkn直接找到最优的参数使得P(OI1A)最大比较困难,但是如果我们知道观察序列◎对应的状态序列Q的话,问题就容易很多了。比如我们需要估计跳转概率ai,它的最大似然估计就是: aii C(i j Zgeo C(一q) 这个公式很符合直觉:要知道从状态i跳转到的概率,首先数一下从i到跳转的次数,然后再除以所有出发的跳转,从而使得二,aj二1。类似的我们可以估计发射概率: 6(up)= zL Ilo,=Dkands,=j Z 11sn 其中函数11s,二刀是indicator函数,如果t时刻的状态为,它的值为1,否则为0。因此分母就是状态出现的次数。类似的, 1to,=weands,-,是t时刻的状态为并且观察是uk,因此分子就是状态为j并且观察是D出现的次数。情景一:若干士兵排成一个队列,每个士兵只能与他相邻的士兵交流,问如何才能使每个士兵都知道总的士兵数?心實典黃覺第显然,对里面的任意一位士兵,他们只能与相邻的人交流传递信息。比如最左边的第一位向第二位传递:第二位左边只有1个。第二位向第三位传递:第三位左边有2个。一直依次传递到最右边最后一位,最后一位获得的信息是他的左边有5个人。但是这个时候只有最右边那个人知道总人数(5+1=6),还不能使其他人知道总人数。其他人只知道他的左边有多少人,右边有多少并不知道。 这个时候怎么办呢? 最右边的人可以再依次往左边传递消息。比如最右边第一位告诉第二位说:第二位的右边只有他1个。依次传递。这样正向和反向各传递-遍,使得每个人拥有两个消息,一个是该士兵的左边有L个人,一个是右边有R个人。总人数=L+R+1。(加上他本人)实例〔编辑〕假设一个学校里有60%男生和40%女生。女生穿裤子的人数和穿裙子的人数相等,所有男生穿裤子。一个人在远处随机看到了一个穿裤子的学生。那么这个学生是女生的概率是多少?使用贝叶斯定理,事件A是看到女生,事件B是看到一个穿裤子的学生。我们所要计算的是P(AIB)。 P(A)是忽略其它因素,看到女生的概率,在这里是40% P(A)是忽略其它因素,看到不是女生(即看到男生)的概率,在这里是60% P(BIA)是女生穿裤子的概率,在这里是50% P(BIA’)是男生穿裤子的概率,在这里是100% P(B)是忽略其它因素,学生穿裤子的概率,P(B)=P(BA)P(A) + P(BA)P(A),在这里是0.5x0.4+ 1×0.6= 0.8.根据贝叶斯定理,我们计算出后验概率P(A/B) , P(BA)P(A) 0.5 × 0.4. P(AB) = P(B) =0.25。 0.8 可见,后验概率实际上就是条件概率。 A:看到女生B:后到一个穿裤子品学生 HMM HMM tate S Obseration D Pso) Pos) p(s) Plo Pals P(s)