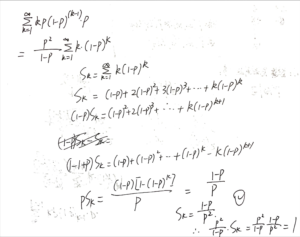This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
本篇笔记的主要内容
本篇笔记的主要内容是：
令人绝望（且最终放弃了的）kalman filter标准公式的推导；
从另一个角度简单理解kalman filter和bayesian filtering.
Geometric Series, Geometric Distributions （等比级数 / 几何级数）
Geometric Series, Geometric Distributions （等比级数 / 几何级数）
最开始在这里看到的：🔗 [论文阅读：《Real-Time Audio-to-Score Alignment of Music Performances Containing Errors and Arbitrary Repeats and Skips》 - Truxton's blog] https://truxton2blog.com/paper_reading_real_time_audio-to-score_alignment_of_music_performances_containing_errors_and_arbitrary_repeats_and_skips/
通过做这道例题判断自己是否遗忘了这方面的知识！
求
[mathjax-d]\sum_{n=1}^{\infty} \frac{2 n}{3^{n+1}}[/mathjax-d]答案
[mathjax]\frac{1}{2}[/mathjax]，见：https://math.stackexchange.com/questions/30732/how-can-i-evaluate-sum-n-0-inftyn1xn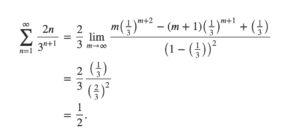
再做一道题：求：
[mathjax-d]\sum_{k=1}^{\infty} k p(1-p)^{(k-1)} p[/mathjax-d]答案
答案就是[mathjax]1[/mathjax]
过程：
其他参考资料：
🔗 [probability - Why does $\sum_{k=1}^{\infty} kp (1-p)^{(k-1)} p$ converge to 1 for all probabilities p? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/3681183/why-does-sum-k-1-infty-kp-1-pk-1-p-converge-to-1-for-all-probabil
更加一般化的公式推导：preview 🔗 [sequences and series - How can I evaluate $\sum_{n=0}^\infty(n+1)x^n$? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/30732/how-can-i-evaluate-sum-n-0-inftyn1xn
其他常见公式总结：preview 🔗 [series.pdf] https://people.math.osu.edu/husen.1/teaching/530/series.pdf
微积分Lim x->0 [log(1+ax)+log(1+bx)]/x
微积分Lim x->0 [log(1+ax)+log(1+bx)]/x
🔗 [Lim x->0 [log(1+ax)+log(1+bx)]/x =? | Socratic] https://socratic.org/questions/lt-x-0-log-1-ax-log-1-bx-x
（几乎没有学进去）继续在kalmanfilter.net上面学习kalman filter
继续在kalmanfilter.net上面学习kalman filter
今天从这里开始：🔗 [State Extrapolation Equation] https://www.kalmanfilter.net/stateextrap.html
要学习STATE EXTRAPOLATION EQUATION，也就是这张图的这个方程：
有点眼熟，是不是和这个差不多？（对应的笔记）
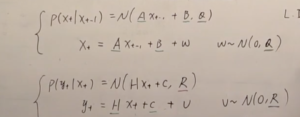
这部分的内容看起来很多，但本质上还是没有引入新的公式，毕竟这是「和物理相关的内容」：
匀加速运动，预测下一时间的位置、速度、加速度。其中加速度保持不变。本质上就是把多个公式融合成了矩阵乘法。
在这个页面的末尾出现了一个新的概念需要学习：Linear Time-Invariant（LTI）（线性时不变）系统。
A time-invariant system is one where a time delay (or shift) in the input sequence causes an equivalent time delay in the system's output sequence.
https://www.kalmanfilter.net/stateextrap.html
接下来看下一章：🔗 [Modeling linear dynamic system] https://www.kalmanfilter.net/modeling.html
先跳过
接下来看下一章：🔗 [Covariance Extrapolation Equation] https://www.kalmanfilter.net/covextrap.html
对比2022-08-07学的入门公式和现在的公式：
等一下！注意到这句话：
covariance matrix和uncertainty有什么关系呢？
🔗 [不确定度与协方差矩阵的关系_linxigjs的博客-CSDN博客] https://blog.csdn.net/linxigjs/article/details/93064354
等等，上面两张图（分别来自CSDN和kalmanfilter.net）的公式是不是有点像？先继续学下去，后续再总结规律。
对这部分证明有所疑惑，但还是先跳过了：
.....
看不下去，跳过了很多章节
再次总结kalman filter的5个基本公式
先看看这个能不能看懂：🔗 [Summary] https://www.kalmanfilter.net/multiSummary.html
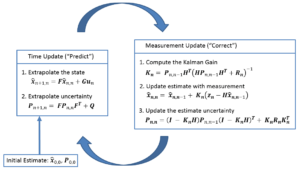
这张流程图的大致思路当然可以看懂，因为沿用了之前学习的[mathjax]\alpha-\beta-(\gamma)[/mathjax]滤波器的思路。
已知的3个学习资料（kalmanfilter.net, B站徐亦达，https://truenobility303.github.io/Filter/）都遇到了麻烦！
从另一个角度简单理解kalman filter
看一下这个：如何通俗并尽可能详细地解释卡尔曼滤波？ - 司南牧(李韬)的回答 - 知乎 https://www.zhihu.com/question/23971601/answer/770830003
对红圈里的文字产生了一点疑惑：
后来想明白了（蓝色高亮文字）：
使用forward algorithm的目的是「把求得的数值拿来用」，当然需要对当前状态进行判定。最简单的方法当然就是「当前时刻哪个状态概率最大就判定为哪个状态」。
接下来是结论：
这部分内容（尤其是Bayesian filtering的引导公式）可能会引起疑惑，补充笔记见：
preview 🔗 [2022-08-02 - Truxton's blog] https://truxton2blog.com/2022-08-02/#（补充）Bayesian_Filtering到kalman_filter过渡的关键公式
