This post was published in 2022-03-19. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
Linux指定进程进行cpu占用监控
比如,监控这个python程序: $ python3 /path/to/run.py :
# xxxxx是PID
# 每5秒更新一次结果
$ pidstat 5 -p xxxxxx
# 更进一步
$ pidstat 5 -p $(ps -f -C python3 | grep "/path/to/run.py" | awk '{print $2}')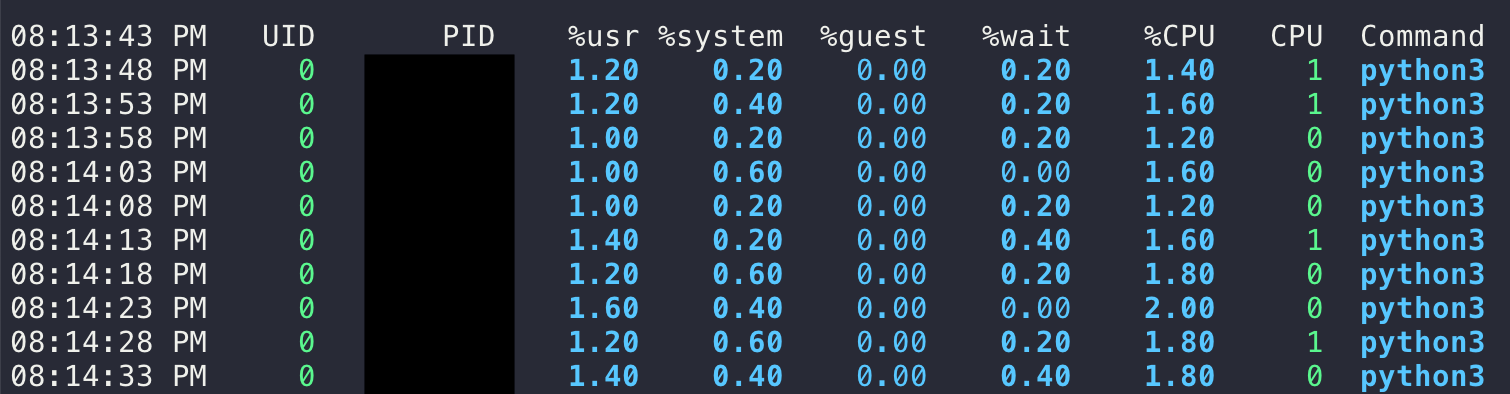
Git repo按修改时间排序文件
学习到了新的git小技巧:
假设这里有一个prismJS的git库:🔗 [prism/components at master · PrismJS/prism] https://github.com/PrismJS/prism/tree/master/components,我的wordpress站点使用了这些代码高亮js文件中的一小部分。出于个人喜好,我习惯定期检查这些文件的更新情况。
在github.com上,这些language-*.js文件都拥有last modified date,但git clone以后这些last modified date都变成了另一个(统一的)时间,很难直接找出“最近修改了哪些文件”。
解决方案:🔗 [Retrieve and set the last modification date of all files in a git repository. Solution for https://stackoverflow.com/a/55609950/4063462] https://gist.github.com/HackingGate/9e8169c7645b074b2f40c959ca20d738#file-restore_last_git_modified_time-sh (stackoverflow原回答)
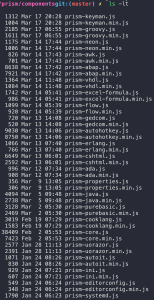
这样就能很容易挑出需要更新的文件了。
备份,防止404
#!/bin/sh -e
OS=${OS:-`uname`}
if [ "$OS" = 'Darwin' ]; then
get_touch_time() {
date -r ${unixtime} +'%Y%m%d%H%M.%S'
}
else
# default Linux
get_touch_time() {
date -d @${unixtime} +'%Y%m%d%H%M.%S'
}
fi
# all git files
git ls-tree -r --name-only HEAD > .git_ls-tree_r_name-only_HEAD
# modified git files
git diff --name-only > .git_diff_name-only
# minus https://stackoverflow.com/questions/1370996/minus-operation-on-two-files-using-linux-commands
# only restore files not modified
comm -2 -3 .git_ls-tree_r_name-only_HEAD .git_diff_name-only | while read filename; do
unixtime=$(git log -1 --format="%at" -- "${filename}")
touchtime=$(get_touch_time)
echo ${touchtime} "${filename}"
touch -t ${touchtime} "${filename}"
done
rm .git_ls-tree_r_name-only_HEAD .git_diff_name-onlyHMM *
主要参考资料:
继续上次(2022-03-02)的内容,阅读以下博客:
🔗 [基于HMM的语音识别(一) - 李理的博客] https://fancyerii.github.io/books/asr-hmm/
🔗 [基于HMM的语音识别(二) - 李理的博客] https://fancyerii.github.io/books/asr-hmm2/
🔗 [基于HMM的语音识别(三) - 李理的博客] https://fancyerii.github.io/books/asr-hmm3/
同时本文slide截图主要来自:🔗 [李宏毅深度学习语音识别(2020最新版)_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1q5411V7tT?p=4
矢量量化(Vector Quantization VQ)
来自:🔗 [基于HMM的语音识别(二) - 李理的博客] https://fancyerii.github.io/books/asr-hmm2/
HMM后续阅读(先丢这里,暂时还没读到)
这篇文章有很多以前没接触过的概念需要学习:🔗 [HMM acoustic modeling -] https://maelfabien.github.io/machinelearning/speech_reco_1/
🔗 [E6820-L10-ASR-seq.fm] https://www.cs.ubc.ca/~murphyk/Software/HMM/E6820-L10-ASR-seq.pdf
三状态HMM
第一次接触是在这里:🔗 [基于HMM的语音识别(三) - 李理的博客] https://fancyerii.github.io/books/asr-hmm3/
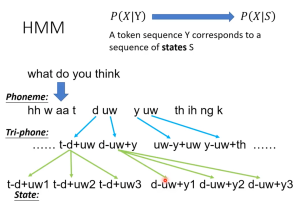
(本文后面有更详细补充)
语音识别:phone (本文后面有更详细补充)
语言(Language)是用于沟通的符号系统。语音(Speech)是由语言产生的声音,唱歌或者汽车的刹车声都不是语音。音素(Phoneme)是语言学的概念,比如/a/就是一个音素,英语有四五十个音素。因子(Phone)是一个声学(Acoustic)概念,表示不同的发音。一个音素可能对于多个不同的发音,比如/t/在”cat”和”stop”的发音是不同的,我们把不同的发音叫做allophone。
https://fancyerii.github.io/books/asr-intro/
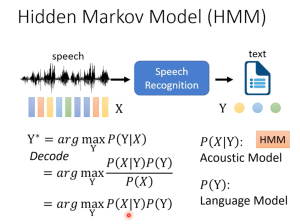
语音识别HMM模型里的“不可观测”到底是什么?
“不可观测“永远是相对于”观测者“(人)而言的:“状态“并不是音频信号,我们只能听到产生的音频特征向量(MFCC),不能听到“状态”。
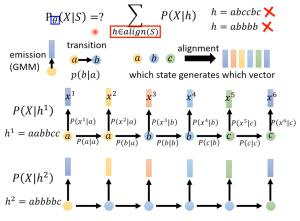
(本图来自李宏毅hmm语音识别,详细内容在本文后面)
从音频分析到NLP处理的全过程
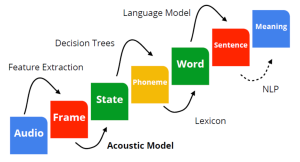
李宏毅 HMM 语音识别
视频:🔗 [李宏毅深度学习语音识别(2020最新版)_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1q5411V7tT?p=4

Phoneme,音素,是发音的基本单位;一个Phoneme会组合前后的phoneme,变成tri-phone,这是因为一个phoneme的发音会受到前后phoneme的影响(*这种现象又被称为协同发音 / Coarticulation);一个tri-phone还会被分得更细致,拥有3个state(s),这就是HMM-GMM模型中使用的state.
从State这里就可以看到“三状态HMM”的模型。为什么是“三状态”?这是语言学家制定的,和44100Hz一样都拥有漫长的历史研究。(其实“五状态”也是可以的)
附:phoneme表,来自 🔗 [1: Phonetic Alphabet for IPA and ARPAbet symbols. | Download Table] https://www.researchgate.net/figure/1-Phonetic-Alphabet-for-IPA-and-ARPAbet-symbols_tbl1_2865098
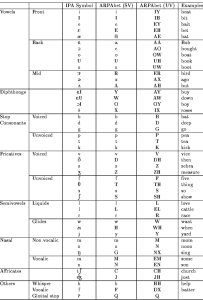
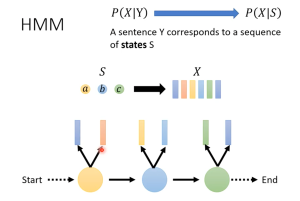
S:state;X: 音频信号Vector
所以就是:每一个state都有可能产生一些音频信号vector片段,把这些state连起来产生的音频信号片段组合就是音频。
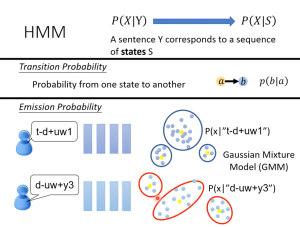
transition probability:从一个state转移到另一个state(也可以是state转移到自身)的概率分布
emission probability:对每一个state,【所有可能】产生的音频信号vector满足一个分布,这就是需要套用GMM模型解决的问题
这就是为什么HMM-GMM模型不使用phoneme作为基本单位,而要使用比phoneme精细的state作为基本单位:对每一个state而言,语言学家要保证它产生的音频信号vector构成一个固定的分布。
假设现在要使用phoneme作为基本单位,考虑这个例子:what do you think(前面的图片里有),对于uw这个phoneme,在do和you里面会产生两个不一样的GMM分布。
那么另一个问题来了:为什么不把一段连续的语音切分成离散的单词形式,然后再对每个单词进行HMM-GMM建模呢?这样是不是可以直接用phoneme了?当然还是很困难/几乎不可行的,因为:

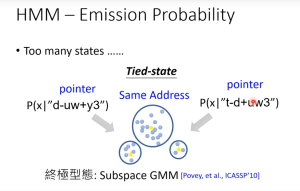
现在的一个问题是:对于语音识别而言,state的可用数量实在是太多了(“假设音子有40个,那么理论上可能有403=64,000403=64,000,实际上英语可能出现的triphone会有50,000左右”. 来源)。所以近10几年还有其他改进的方法(比如subspace GMM)来处理这个问题。

这就是HMM模型中“hidden”所代表的内容:state(s)的排列方式(当然需要正确的排列方式)。
所以最后HMM-GMM模型解决语音识别问题的步骤就变成了:穷举所有可能的排列方式,找出最后可能的那种排列方式。当然这个穷举空间实在是太大了,所以这种方法仅仅是学习理论所用。
由于这个视频课程的主要内容是深度学习语音识别,所以HMM的内容就到这里停止了。当然传统HMM-GMM模型的内容远不止这些,所以本视频的作用是“正确理解HMM-GMM模型的建模意义”。
MFCC的生理学意义
阅读本文开头几段即可:🔗 [MFCC特征提取教程 - 李理的博客] https://fancyerii.github.io/books/mfcc/
不严谨地,可以这样描述:
从256个离散音频信号到39维的MFCC,MFCC用39维的数组来描述各个人体发音器官(唇/齿/舌)的 开/闭/半开... 等状态。
viterbi, viterbi training, soft EM, hard EM, k-means, Baum-Welch
后续补充:更详细的内容参考这篇:🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/
阅读这篇文章,以及这篇文章的时候发现了viterbi training/hard EM/soft EM这样的概念。

所以:
1,viterbi training又被称为hard EM,它是由多个viterbi动态规划算法反复进行参数迭代得到最优结果的一种EM算法;
1.5,Viterbi training没有使用GMM模型,它直接对离散的观察数据进行概率计数统计;
2,Baum-Welch又被称为soft EM,它是viterbi training的改良版;
2.5,Baum-Welch使用了GMM模型;
3,k-means也是一种特殊的hard EM算法(来源)
本日最后总结,HMM-GMM模型流程(之一)

目前看来对这个流程的理解仍然很模糊,所以需要在接下来的garbage草稿里继续理解这个问题。(见:🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/)
OCR辅助查找工具
HMM P(XIY) PXS) A token sequence Y corresponds to a sequence of states S what do you think Phoneme: hh w aat d uw y UW th ih ng k Tri-phone: t-d+uw d-uw+y uw-y+uw y-uw+th t-d+uw1 t-d+uw2 t-d+uw3 d-iw+y1 d-uw+y2 d-uw+y3 State: Ha(xIS) =? P(X h) h = abccbc healign(S) h = abbbb父 transition emission alignment Q (GMM) a+b p(bla) which state generates which vector P(Xlh) h1 aabbcc Tperlo) perio) Tpaeiy Tpastb Toesio Peto a P(ala) P(bla) P(blb) P(clb) P(clc) P(XIh2) _LL1_1 h2 = abbbbc Language Model Meaning Decision Trees Sentence Feature Extraction Word Phoneme NLP State Frame Lexicon Audio Acoustic Model Hidden Markov Model (HMM) speech text Speech Recognition X Y Y* = arg max P(YIX) P(XIY): HMM Decode Y P(XIYP(Y) Acoustic Model二arg max Y P(X) P(Y): = arg max P(XIY)P(Y) Language Model Y HMM PXY) PXIS) A token sequence Y corresponds to a sequence of states S what do you think Phoneme: hh w aa t Uw y uw th ih ng k Tri-phone: t-d+uw d-uw+y uw-y+uw y-uw+th t-d+uw1 t-d+uw2 t-d+uw3 d-uw+y1 d-uw+y2 d-uw+y3 State: p EI L 13 | d cL 2 2 S e 1277 a 8 §l 8 LIn E e Iden e tal 2 178 4 19 - 3 all L 18 d 18 1 & s 13 00 8: 00 P pe 3 Lee On + 3 F .% an O 9 g & 8 8 19 g & B A--OR@ @ sop== x4/30x07 00 0+ - ›O AN -H O n 1 n 3 incl 5 -. l 8 P S H e Ren s Canno l 118 68 & 3 n 619 N M4 ‹ Ic 1’6 un 5 E ‘ 2 L o 89 c O la 53 E 32=45339655471468-20-4-505-805-8=35 =7≥365=350 6043: 6-00800+44 - XO 00 48 5 e Absinahßondeesedededeksdesiden.detnronindininel E 9 d e e 3 895-022058 < 28 - -- s - IT I e Ze cen E - -B 8-E-98:304 g gen 8§ g le S a 8 a g To- A S 8 Lil 44 a P(X]S) HMM P(X|Y) A sentence Y corresponds to a sequence of states S S X a 11 Start End HMM P(X|Y) P(X]S) A sentence Y corresponds to a sequence of states S Transition Probability Probability from one state to another *b p(b|a) Emission Probability t-d+uw1 P(x|”t-d+uw1”) Gaussian Mixture Model (GMM) d-uw+y3 P(x|”d-uw+y3”)当然我们可以用人来标注每个时刻对应哪个状态,但是要人来标注这种对齐是非常困难而且容易出错的。因为很多音素的边界是很难区分,比如下图,让非专业的人通过看波形或者频谱是很难准确的区分其边界的。 Speech recognition: The input can be a spectrogram or some other frequency based feature extractor. HMM - Emission Probability Too many states Tied-state pointer pointer Same Address P(xI”d-uw+y3” P(xI”t-d + LW 3”) 終極型態:Subspace GMM Povey, et al., ICASSP’10] PaX|S) : P(X]h) h = abccbc hEalign(S) h = abbbb transition alignment emission a-~b (GMM) p(b|a) which state generates which vector 21 * x x4 25 x’ P(X]h+) P(x*|5) h1 = aabbcc parta) Proray x4|b) porto prono a P(ala) a b P(b|a) P(b|b) P(c|b) P(c|c) P(X]h2) . _LL_Li h2 = abbbbc现在的问题是我们并不知道观察◎对应的状态序列。回忆一下前面的解码问题:如果我们知道模型的最优参数,那么我们可以使用Viterbi算法找到“最优”的状态序列,假如有了这个状态序列,我们就可以估计模型的最优参数。这似乎是一个鸡生蛋蛋生鸡的问题一一知道模型参数就可以通过Viterbi算法找到隐状态,知道隐状态就可以学习模型参数。 现在两者都不知道怎么办?我们可以先随机初始化一组模型参数,根据这组模型参数估计最优的状态序列;有了状态序列,我们又可以最大似然估计模型的参数。可以证明(但这里不会证明))新的模型参数要比之前的更好,这样我们就可以不断的循环这个过程一一用新的模型参数再去求最优序列,然后再用新的状态序列估计更新的参数。直到新参数和旧参数一样才停止,实际的停止条件是超过一定迭代次数或者新1旧参数差不多。这个时候可以证明我们找到了局部最优的解(但不是全局最优解)。 注意:上面描述的算法通常叫作Viterbi训练算法。那什么是前向后向算法?它和Viterbi算法有什么区别? Viterbi训练算法的问题在于它会为每一个时刻找一个固定的“最优”的状态,但很多时候某个观察到底是属于哪个状态是很难确定的。尤其在迭代的早期,本来模型就不好,用它来找到的“最优”状态序列就不准,然后用不准的状态来估计模型参数就更不准了。所以更好的办法是用当前的模型计算每个时刻的状态的概率分布,这样可以避免前面的问题。那怎么计算每个隐状态的概率分布呢?这就需要用到前向后向算法了。我们最后总结一些使用训练HMM-GMM声学模型的过程: 首先初始化一个flat-start的monophone的单高斯模型用EM(前向后向)算法估计参数把训练数据的monophone扩展到triphone,把单高斯的monophone模型的参数作为triphone参数的初始值用EM算法重新估计triphone模型的参数使用决策树对triphone的状态进行聚类,然后再用EM算法对聚类后的状态再进行参数重估计