WARNING: This article may be obsoleteThis post was published in 2022-02-28. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
继续复习C语言（鸽了）
花了一段时间纠正了昨天笔记中的严重错误：关于C语言array在内存中的分配问题。
多维数组
（可能要鸽）
复习马尔可夫
复习：🔗 [2021-12-21 - Truxton's blog] https://truxton2blog.com/2021-12-21/
时间长了有所遗忘，对这张图产生了疑问：https://truxton2blog.com/wp-content/uploads/2021/12/20211221_170350_v3ycl-768x582.jpg，但其实这张图应该没有什么大问题（还是要多看浙大概率论对Markov的基本定义）
复习：隐马尔可夫-Viterbi算法：🔗 [2022-01-18 - Truxton's blog] https://truxton2blog.com/2022-01-18/ 补充了一道例题（https://truxton2blog.com/wp-content/uploads/2022/03/20220301_081738_YgCjq.pdf）
HMM: Baum-Welch算法（讨论和Viterbi的区别）
注意：下面这些笔记讨论得太浅显了，几乎没有参考价值，更具体的笔记见：🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/
注意：Viterbi和Viterbi training是不一样的，见：🔗 [2022-03-19 - Truxton's blog] https://truxton2blog.com/2022-03-19/
区别于之前学习的Viterbi算法，本文主要比较它们的不同
这两个算法解决的是两个不同类型的问题：
Baum-Welch算法解决的是学习问题；Viterbi算法解决的是预测问题。
当然这样解释并不是100%令人信服（两种算法的输入输出存在一些交集），所以还需要更仔细地查找它们的不同之处：
🔗 [machine learning - What are the differences between the Baum-Welch algorithm and Viterbi training? - Cross Validated] https://stats.stackexchange.com/questions/581/what-are-the-differences-between-the-baum-welch-algorithm-and-viterbi-training
以及：🔗 [hidden markov models - Viterbi training or Baum-Welch algorithm to estimate the transition and emission probabilities? - Stack Overflow] https://stackoverflow.com/questions/13360892/viterbi-training-or-baum-welch-algorithm-to-estimate-the-transition-and-emission
以及：🔗 [lsa352.lec7.ppt] https://nlp.stanford.edu/courses/lsa352/lsa352.lec7.6up.pdf
从上面的回答可以看出，尽管Baum-Welch要求的输入数据没有Viterbi多（Viterbi需要已知完整的模型[mathjax]\lambda=(A, B, \pi)[/mathjax]），但在绝大多数情况下，Baum-Welch算法的准确率反而更高（这听起来似乎有些反常理，但确实如此）。所以目前得到的结论是：
尚未解决的问题（更新：已解决）
🔗 [HMM acoustic modeling -] https://maelfabien.github.io/machinelearning/speech_reco_1/#introduction-to-hmm-gmm-acoustic-modeling ，这里出现了一些新概念需要区分：
hard EM, soft EM, Viterbi EM
当然这些问题还是解决了，见：🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/
乐理的中英文对照 *
前几次的内容：🔗 [You searched for 乐理 - Truxton's blog] https://truxton2blog.com/search/乐理/
另外找到了一个中英文对照总结：🔗 [音乐术语英文名称汇总（一） - 知乎] https://zhuanlan.zhihu.com/p/35999407
又找到了一个中英文对照总结：🔗 [音乐术语列表 - 维基百科，自由的百科全书] https://zh.wikipedia.org/zh/音乐术语列表
转调：transposition，“ ... a concept used in music to shift a melody or an entire piece of music to another key ...” （《fundamentals of music ....》）
音程：interval，“In music, an interval may be loosely defined as the difference between two pitches. The most basic interval in music is the octave.” （《fundamentals of music ....》）
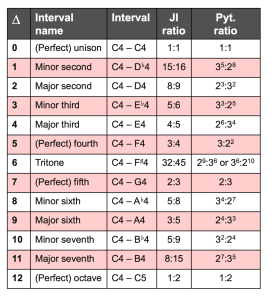
音阶/音级：scale/musical scale，“a scale can be regarded as a set of notes, where the elements are typically ordered by ascending pitch” （《fundamentals of music ....》）
staccato 断音，断奏
Computer Vision论文阅读
🔗 [ResNet变体：WRN、ResNeXt & DPN - 知乎] https://zhuanlan.zhihu.com/p/64656612
🔗 [WRNS：Wide Residual Networks 论文笔记_小时候贼聪明-CSDN博客] https://blog.csdn.net/wspba/article/details/72229177
OCR辅助查找工具
隐马尔可夫模型由初始状态概率向量丌、状态转移概率矩阵A和观测概率矩阵B决定。〔和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型入可以用三元符号表示，即入=(A, B,元) (10.7) A,B,T称为隐马尔可夫模型的三要素。状态转移概率矩阵A与初始状态概率向量个确定了隐藏的马尔可夫链，生成不可观测的状态序列。观测概率矩阵B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。 10.1.3隐马尔可夫模型的3个基本问题隐马尔可夫模型有3个基本问题： (1）概率计算问题。给定模型入=(A,B,r）和观测序列(ol,o2,⋯，07)，计算在模型入下观测序列◎出现的概率P(OIA)。 10.2概率计算算法197 (2）学习问题。已知观测序列◎=(o1,02，⋯,o7)，估计模型入=（A,B,T）参数，使得在该模型下观测序列概率P(OIA)最大。即用极大似然估计的方法估计参数。 (3）预测问题，也称为解码(decoding）问题。已知模型入=（A,B,元）和观测序列◎=(o1,02，⋯，07)，求对给定观测序列条件概率P(IIO)最大的状态序列[二(l,i2,，)。即给定观测序列，求最有可能的对应的状态序列。 Viterbi Training Much faster than Baum-Welch But doesn’t work quite as well But the tradeoff is often worth it. Primus Secundus Tertius Quartus Quintus Sextus Septimus Octavus Fist Second Third Fourth Fifth Sixth Seventh Eighth (a) C4 D4 E4 F4 G4 A4 B4 C5 Perfect Augmented Minor Major Augmented Minor Major Perfect Tritone unison unison second second second third third fourth (b) A=0 A A=1 A=2 A=3 A=3 A=4 A =5 A=6 Diminished Perfect Augmented Minor Major Augmented Minor Major Perfect fifth fifth fifth sixth sixth sixth seventh seventh octave A=6 1 =7 A=8 A=8 A=9 A= 10 A=10 A= 11 A=12 Fig. 5.2 (a) C major scale and enumeration of its constituent notes using ordinal numbers (in Latin and English). (b) Score representation of various intervals. Because of enharmonic equivalence, there may be musically different intervals having the same distance 4 (given in semitones). Interval Interval J Pyt. name ratio ratio (Perfect) unison C4 C4 1:1 1:1 Minor second C4 - Db4 15:16 35:28 2 Major second C4 - D4 8:9 23:32 Minor third C4 -Eb4 5:6 33:25 Major third C4 - E4 4:5 96.24 5 (Perfect) fourth C4 - F4 3:4 3:22 Tritone C4 -F#4 32:45 29:36 Or 36:210 7 (Perfect) fifth C4 - G4 2:3 2:3 8 Minor sixth C4 -Ab4 5:8 34:27 Major sixth C4 A4 3:5 24:33 10 Minor seventh C4 - Bb4 5:9 32:24 11 Major seventh C4 B4 8:15 27:35 12 (Perfect) octave C4 - C5 1:2 1:2
