WARNING: This article may be obsoleteThis post was published in 2022-06-22. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
本篇笔记总结
本篇写的很跳跃且很乱，主要学习了一个（实际上很简单的）Viterbi空间压缩优化算法；最后得出的结论见：文末。
继续学习Viterbi
首先还是复习一遍经典老题：🔗 [2022-01-18 - Truxton's blog] https://truxton2blog.com/2022-01-18/#隐马尔可夫-Viterbi
值得注意的是，这道题很容易犯错，看来还是不够熟练，需要每次都做一遍。
顺便搞点笔记：
接上面的PDF笔记可知，常规Viterbi所需要占用的空间为[mathjax]m \times n[/mathjax]. （[mathjax]m[/mathjax]为state数量，[mathjax]n[/mathjax]为时间）
更高效（节省空间）的改进型Viterbi算法
🔗 [[0704.0062] On-line Viterbi Algorithm and Its Relationship to Random Walks] https://arxiv.org/abs/0704.0062
本篇论文的主要作用在于：
1：压缩空间
2：on-line Streaming Viterbi：
这个总结很重要，为什么on-line viterbi不容易实现？因为（传统viterbi算法）越到后面，每新增一次observe数据，都要从头推算optimal path，这也就意味着程序需要存储全部路径！如果我们能找到很多「Coalescence point」，就能每次都从「Coalescence point」开始切片，这样就省去了大量存储空间和计算时间。
这是论文里的一张Viterbi表格图：
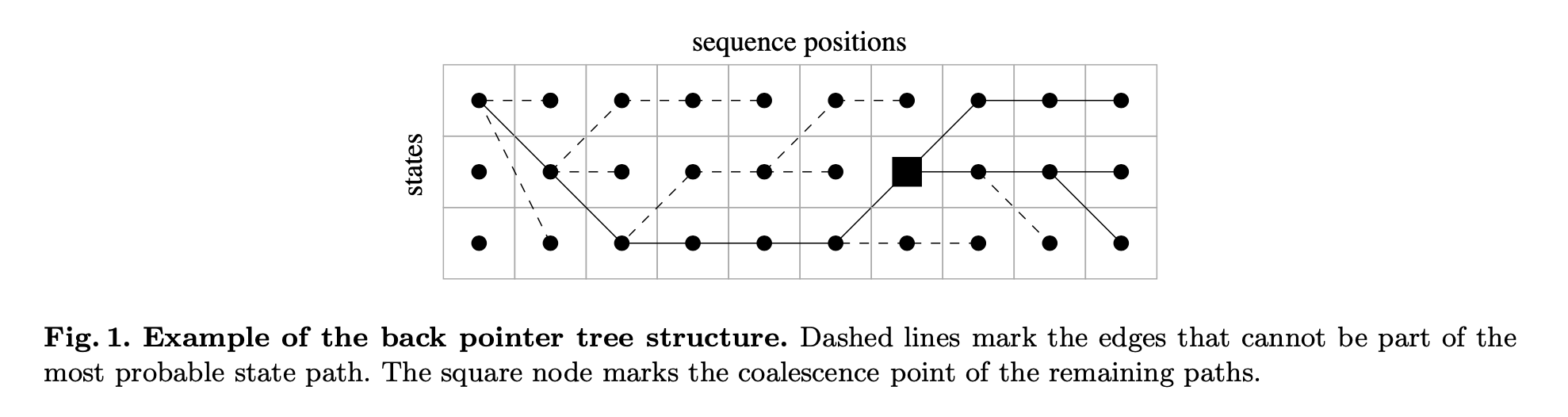
等等，仔细观察上面这张图：这张图里的「虚线」是不是少画了几条？并没有。重复Viterbi graph的特质：“每个子节点都必须指向唯一的1个父节点”，所以虚线并没有少画！
先做一点预先笔记：
但是上面这条笔记和论文里的内容还不一样，论文里的discard更狠，但是需要找出一个「Coalescence point」.
等等，有一篇更老的论文讲述这个，见：🔗 [viterbi_algorithm.pdf] https://www2.isye.gatech.edu/~yxie77/ece587/viterbi_algorithm.pdf
是的！首先，由过去的笔记可知，Viterbi Algorithm本质上是一个MAP算法。
前置知识：K-best Viterbi Algorithm
来自：🔗 [thesis.pdf] https://uwspace.uwaterloo.ca/bitstream/handle/10012/4603/thesis.pdf
可以参考：🔗 [解码算法：N-best viterbi - 知乎] https://zhuanlan.zhihu.com/p/83525045
再等等，本篇笔记最开始的论文 🔗 [On-line Viterbi Algorithm and Its Relationship to Random Walks] 就是为了找那个「Coalescence point」的，暂时不需要其他论文的算法，还是先看完这篇论文吧。
有点难理解，还是再看看[The Viterbi Algorithm]吧。
注明：下面这个网页没啥新鲜的东西，反而多了一些奇怪疑惑的内容。
再找到一个教学网页：🔗 [Title Page] http://www.cim.mcgill.ca/~latorres/Viterbi/va_title.htm
首先就遇到了一个非常令人疑惑的东西：
临时查阅了这个概率论复习PPT：🔗 [§1.5 条件概率] https://web.xidian.edu.cn/lnzhu/files/20180912_200706.pdf
由于上面那个网页没什么用，现在重新回到资料[2]：
先放一个资料在这里，以后有机会再看：
🔗 [beam search 和viterbi对比] https://puluwen.github.io/2019/01/beam-search-vs-viterbi/
下面2张图来自李宏毅2020语音识别课程：（从p3第28分钟开始：🔗 [[DLHLP 2020] 李宏毅老师2020春课程-语音识别-语音合成-语音分离_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1hZ4y1w7j1?p=3）（另：对这门课的入门部分总结博客可以看这里）
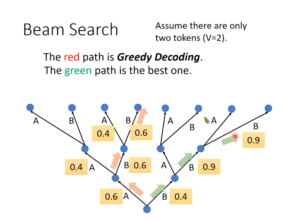
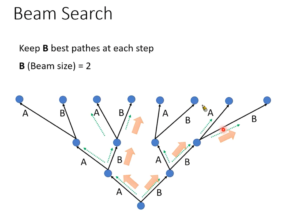
可以看到，beam search和k-best Viterbi有一点...相似。
那么beam search和k-best Viterbi到底有什么区别呢？还是说它们就是同一个算法？
等等！在搜寻资料的过程中又发现了「A* 搜索算法」，见： 🔗 [A*搜尋演算法 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/A*搜尋演算法 ，以及这个解释得更清楚的博客：🔗 [A*搜索 · ACM Book] https://hrbust-acm-team.gitbooks.io/acm-book/content/search/a_star_search.html
资料1：🔗 [ACL12_decoding.pdf] http://www.yichang-cs.com/yahoo/ACL12_decoding.pdf
资料2：🔗 [natural language - What is the difference between the Viterbi algorithm and beam search? - Cross Validated] https://stats.stackexchange.com/questions/536249/what-is-the-difference-between-the-viterbi-algorithm-and-beam-search
来自资料2的结论：是的，如果算力足够，把beam search的存储空间设置为HMM state space，那么它们两者是一样的。
这也印证了下面的结论：
seq2seq的简单介绍
这篇文章非常容易理解：🔗 [一文看懂 NLP 里的模型框架 Encoder-Decoder 和 Seq2Seq] https://easyai.tech/ai-definition/encoder-decoder-seq2seq/
浏览资料有点偏离大主题了，现在重新回到重点：「如何寻找那个Coalescence point」？
不妙，我好像想太多了，「Coalescence point」是不是可以直接判断出来？如果某个时间点上的所有节点都指向同一个父节点，那么就可以删掉父节点之前的存储空间，从父节点开始计算...至于Coalescence point到底有多大几率出现，那就是另一个问题了，但至少我们简化了很多东西！
所以现在的算法就变成了这个样子：
- 首先执行一个最常规的Viterbi算法；
- 算法进行过程中突然发现：时间[mathjax]t[/mathjax]里的所有节点都指向同一个父节点（把这个父节点称为 Coalescence point ）；
- 把[mathjax]t-1[/mathjax]之前的所有Viterbi graph全部丢弃，继续进行Viterbi算法；
- 其余内容保持不变，但整个过程大大节省了存储空间和back tracking消耗的时间。 Coalescence point 找的越多就越节省空间和时间。
所有阅读过的资料
[1] On-line Viterbi Algorithm and Its Relationship to Random Walks: https://arxiv.org/abs/0704.0062
[2] The Viterbi Algorithm: https://www2.isye.gatech.edu/~yxie77/ece587/viterbi_algorithm.pdf
[3] Viterbi Algorithm in Text Recognition: http://www.cim.mcgill.ca/~latorres/Viterbi/va_title.htm
