WARNING: This article may be obsoleteThis post was published in 2022-08-02. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
从Edge换回Chrome
上一次是从chrome换到edge：🔗 [2021-11-20 - Truxton's blog] https://truxton2blog.com/2021-11-20/
用了半年多以后，又一次从Edge换回了Chrome，主要原因是：
明明是chromium内核的浏览器，edge却死活不肯支持avif格式的图片，令人感到非常失望；
最近Edge打开PDF特别卡，严重影响了使用体验；
有很长一段时间Edge打开bilibili的部分视频会中途卡住，不得不使用Safari播放，现在换到Chrome再试一段时间。
2023年1月：我已经差不多忘记Edge了，今天偶然发现Edge还是不支持avif格式的图片。
今天从哪里开始？Bayesian Filtering
今天从哪里开始？
昨天刚刚完结了bayesian network - introduce，今天不知道该从什么地方继续了（）
决定：从这里继续：一篇没有发表的笔记，因为几乎没有任何内容 🔗 [2022-07-24 - Truxton's blog]
卡尔曼滤波器！
🔗 [卡尔曼滤波与隐马尔可夫模型 - TrueNobility303] https://truenobility303.github.io/Filter/
Filtering, smoothing and prediction
滤波，平滑和预测
思路有点散乱，先贴点链接：
preview 🔗 [Lars Hammarstrand - YouTube] https://www.youtube.com/channel/UCI9oKvg_1Q2-JpKGwMp4Peg/videos
🔗 [3.1 Filtering, smoothing and prediction - YouTube] https://www.youtube.com/watch?v=pVyltJnXlAI
* 下面的内容从笔记p=7733整合进来
从这里开始：🔗 [卡尔曼滤波与隐马尔可夫模型 - TrueNobility303] https://truenobility303.github.io/Filter/
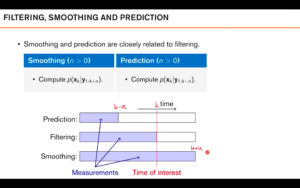
注意下面的图：
虚线标注的「time of interest」只是「我们希望研究的时间点（的状态）」；
紫色条对应的是「已经走过的时间」，很显然，紫色条的最右端为「当前的时刻」。
那么prediction就是「采集所有时序数据，但希望对未来的某个时间点（的状态）进行推测」；
filtering就是「采集所有时序数据，对当前时间（的状态）进行推测」；
smoothing就是「采集所有时序数据，对过去的某个时间点（的状态）进行推测」。
和这个知乎回答的内容要保持逻辑一致。
🔗 [滤波、预测和平滑之间的关系是什么？ - 知乎] https://www.zhihu.com/question/24877642
还有一个答案（核心内容是完全一致的，多一个补充）
🔗 [贝叶斯滤波（Bayesian filtering） - 知乎] https://zhuanlan.zhihu.com/p/139215491
和已学过的马尔可夫家族成员的联系
和一些学过的马尔可夫家族成员的联系：
滤波，filtering，利用当前观测到的所有结果推测当前的状态：对应Forward algorithm；
平滑，smoothing，利用当前观测到的所有结果推测过去某一时刻的状态：可以是Forward-backward，也可以是viterbi. 注意单独backward是不行的，因为「要观测所有结果」。
预测，prediction，利用当前观测到的所有结果推测未来某一时刻的状态：看起来还没接触过，但实际上接触过！在bayesian filtering的一个子步骤中，我们首先会对下一刻时间的状态进行先验预测，然后等“下一刻”到来之时，用观测出的结果更新我们的先验预测。红字的部分即为prediction .
写得差不多了，可以回来了，现在开始学习「贝叶斯滤波」
Parameters of interest / nuisance parameter
parameters of interest / nuisance parameter
🔗 [NARUTOACM-概率统计学相关笔记（八）] http://narutoacm.github.io/2014/09/19/prob-stati-notes8.html
Bayesian filtering
bayesian filtering
* 又称为recursive Bayesian estimation
滤波：采集到目前为止的数据，对当前时刻的状态进行推测。
阅读这部分内容：
但这一步拖了我非常长的时间：
.....
.....
.....
终于，过了很长时间我才差不多搞明白，可以回来继续写笔记了。
标题写成bayesian filtering，但目前看来，要想成功推导原博客里的公式，必须认定这是一个markov chain模型！
查了一下似乎大家都喜欢这么干：
同时，维基百科对bayesian filtering也是这样直接声明为markov process的：
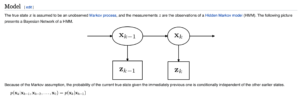
有了Markov chain的额外条件，现在终于可以推导出来了：
* 上面这个推导过程中有一个“如何正确拆分[mathjax]P(A, B, C)[/mathjax]”的问题，可以参考这张图：
似乎很像...Forward Algorithm！
通过对比2个wikipedia的公式：
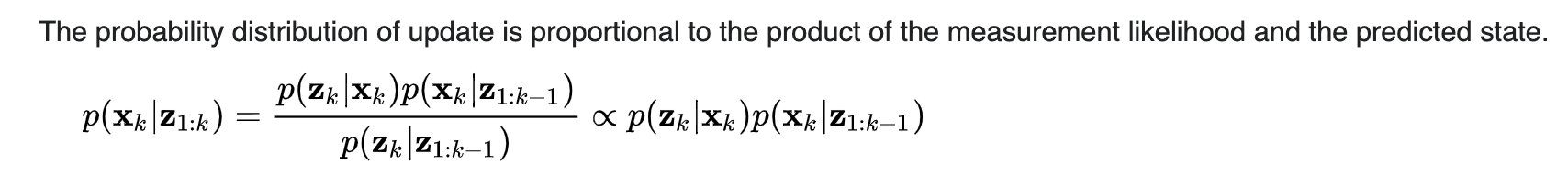
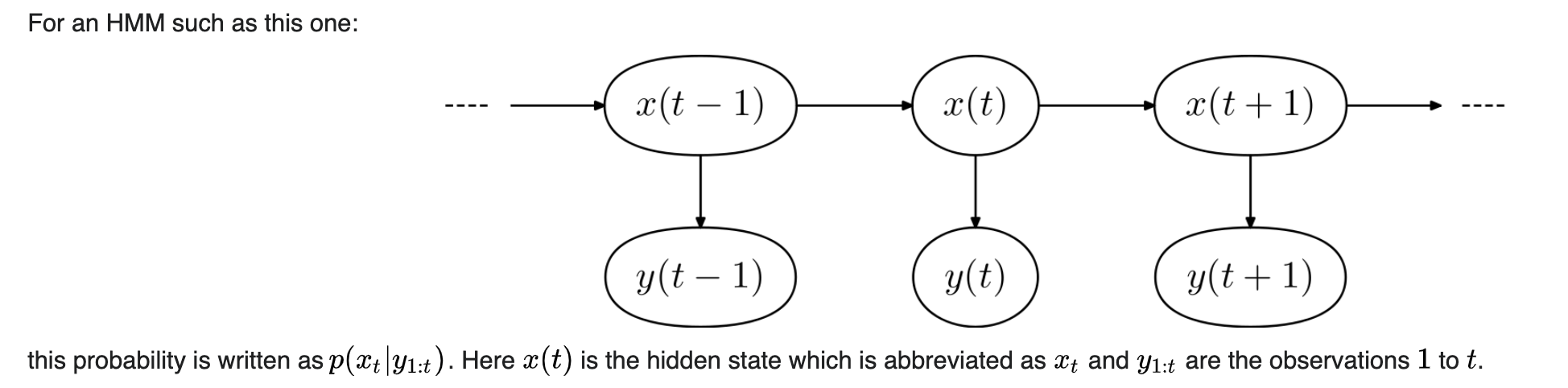
所以目前的结论就是：我发现过去的笔记又写错了，很生气，大改了一通：
🔗 [2022-03-20 - Truxton's blog] https://truxton2blog.com/2022-03-20/#笔记1
Bayesian filtering的prior和posterior
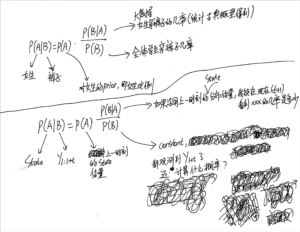
首先从最基本的贝叶斯公式开始：
在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率（Posterior probability）是在考虑和给出相关证据或数据后所得到的条件概率。同样，后验概率分布是一个未知量（视为随机变量）基于试验和调查后得到的概率分布。
https://zh.m.wikipedia.org/zh-hans/后验概率
在收到消息之前有个大致的估计，这是prior -> 又收到了某个消息 -> 更新了相关数据后得到新的概率分布，这是posterior
然后考虑刚刚学过的bayesian filtering：
prior -> 又观测到了新东西 -> 更新了对当前状态的估计，这是posterior
还是准备从最经常使用的一个例子开始：
然后推导到本篇笔记所学习的bayesian filtering：
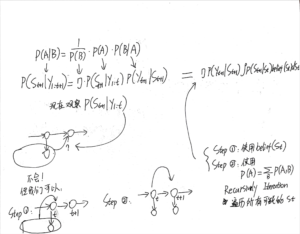
最后总结bayesian filtering的prior、posterior迭代顺序：
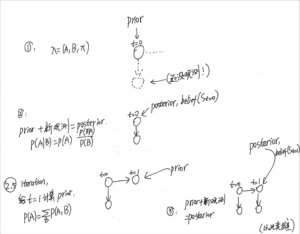
总之，就是一个不断循环的过程：先做prediction（使用先验prior），然后根据实际观测值修正模型（使用后验posterior），然后继续移动到下一个时间点...
（补充）Bayesian Filtering到kalman filter过渡的关键公式
2022-08-11补充内容
🔗 [【易懂教程】我是如何十分钟理解与推导贝叶斯滤波(Bayes Filter)算法？ - 知乎] https://zhuanlan.zhihu.com/p/75880143
[mathjax-d]P\left(x_{t} \mid z_{t}, u_{t}, x_{t-1}\right)=\eta P\left(z_{t} \mid x_{t}\right) P\left(x_{t} \mid u_{t}, x_{t-1}\right)[/mathjax-d]对比不含[mathjax]u[/mathjax]的公式（推导在后面）：
[mathjax-d]P\left(X_{t} \mid Z_{t}, X_{t-1}\right)=\eta\ P\left(Z_{t} \mid X_{t}\right) P\left(X_{t} \mid X_{t-1}\right)[/mathjax-d]这个公式就是bayesian filtering和kalman filter的核心部分。
注意到多增加了一个变量：[mathjax]u[/mathjax]，它是「从t-1到t所进行的动作」。
总之现在多了一些东西，但总体推导方式还是不变的，具体内容：
另外，如果要推导不含[mathjax]u[/mathjax]的公式也可以利用相似的方法（在本篇笔记之前应该推导过了，但还是再推导一次）：
试图过渡到Kalman，但没有完成
* 试图在一天之内从bayesian filtering过渡到kalman filter，但发现根本学不会，只能另开一篇笔记慢慢学了。下面记录了一些学习过程：
接下来是kalman filtering
以及：
稍微复习一下高斯过程：🔗 [2021-11-18 - Truxton's blog] https://truxton2blog.com/2021-11-18/#高斯过程
* 下面的内容好像有点问题，先划掉
今天的笔记暂时不推导kalman filter了，但一定要记住一点：
kalman filter的 Gaussian 表现在“预测状态的概率分布是Gaussian”，而不是GMM模型里的“发射概率是Gaussian mixture model“.
preview 从这里开始看：🔗 [Kalman filter - Wikipedia] https://en.wikipedia.org/wiki/Kalman_filter#Relationship_to_recursive_Bayesian_estimation
🔗 [4.2 Bayesian derivation of the Kalman filter - YouTube] https://www.youtube.com/watch?v=u_xRUxwlaFY
好久没看GP了，复习起来非常头大。
给2021-11-18更新了一些笔记，现在看起来更容易入门了：
现在还是搞不懂的一个问题就是：kalman filter有哪些变量是Gaussian？有没有可能包含GMM？
