This post was published in 2021-10-22. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
2022-08-20补充笔记
2022-08-20,我把本篇笔记又复习了一遍,很多例题进行了重新推导计算(已经生疏)。2022-08-20的笔记与本笔记之间是互补关系。见:🔗 [2022-08-20 - Truxton's blog] https://truxton2blog.com/2022-08-20/
Bayesian Inference/贝叶斯推断(包含一些基础概率论知识)
Bayesian Inference/贝叶斯推断
从这个视频开始:🔗 [How Bayes Theorem works - YouTube] https://www.youtube.com/watch?v=5NMxiOGL39M , 接下来出现的一系列⚫️内容都和该视频相关,且出现顺序和视频基本一致。
⚫️ 复习正态分布:
[mathjax-d]f(x|\mu,\sigma^2)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}}[/mathjax-d]重要性质:[mathjax]\text{mean/median: }\mu[/mathjax]; [mathjax]\text{variance: }\sigma^2[/mathjax].
⚫️ 复习条件概率:🔗 [2021-09-29 - Truxton's blog] https://truxton2blog.com/2021-09-29/
⚫️ 复习联合概率:
[mathjax]P(A\ \text{and}\ B)[/mathjax] is the probability that both [mathjax]A[/mathjax] and [mathjax]B[/mathjax] are the case.
Also written [mathjax]P(A, B)[/mathjax] or [mathjax]P(A \cap B)[/mathjax].
[mathjax-d]P(A\ \text{and}\ B)=P(B\ \text{and}\ A)[/mathjax-d]⚫️ 复习边缘概率
假设有概率分布[mathjax]P(x,\ y)[/mathjax], 那么有边缘分布:
[mathjax-d]P(x)=\sum_{y} P(x, y)=\sum_{y} P(x \mid y) P(y)[/mathjax-d]⚫️ 联合概率、边缘概率与条件概率之间的关系
[mathjax-d]P(X=a \mid Y=b)=\frac{P(X=a, Y=b)}{P(Y=b)}[/mathjax-d]
⚫️ 上述内容的总结博客:🔗 [联合概率、边缘概率、条件概率之间的关系&贝叶斯公式_tick_tock97的博客-CSDN博客_联合概率] https://blog.csdn.net/tick_tock97/article/details/79885868
⚫️ standard deviation 和 standard error
standard deviation:
[mathjax-d]\sigma=\sqrt{\frac{1}{N}\left[\left(x_{1}-\mu\right)^{2}+\left(x_{2}-\mu\right)^{2}+\cdots+\left(x_{N}-\mu\right)^{2}\right]}, \text { where } \mu=\frac{1}{N}\left(x_{1}+\cdots+x_{N}\right)[/mathjax-d]standard error:
[mathjax-d]\sigma_{x}^{-}=\frac{\sigma}{\sqrt{n}}\ , \sigma : \text{standard deviation}[/mathjax-d]⚫️ bayesian theorem
[mathjax-d]P(A \mid B)=\frac{P(B \mid A) \cdot P(A)}{P(B)}[/mathjax-d]❓ ⚫️ marginal likelihood
⚫️ 如果bayesian prior取uniform分布,那么计算得到的MLE=MAP,见视频16:30开始。
🔗 [machine learning - How does a uniform prior lead to the same estimates from maximum likelihood and mode of posterior? - Cross Validated] https://stats.stackexchange.com/questions/64259/how-does-a-uniform-prior-lead-to-the-same-estimates-from-maximum-likelihood-and
接下来学习这个视频:🔗 [Bayesian Inference: An Easy Example - YouTube] https://www.youtube.com/watch?v=I4dkEALQv34
⚫️ 中心极限定理
🔗 [中心极限定理 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/%E4%B8%AD%E5%BF%83%E6%9E%81%E9%99%90%E5%AE%9A%E7%90%86
⚫️ 点估计/point estimation
这道例题的答案在下面;
首先可以入门点估计的一些例题:🔗 [参数估计之点估计(矩估计,最大似然估计) 详解+例题_Joker-Tong的博客-CSDN博客最大似然估计法例题] https://blog.csdn.net/Weary_PJ/article/details/106525960
⚫️ 泊松分布
🔗 [泊松分布 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/%E5%8D%9C%E7%93%A6%E6%9D%BE%E5%88%86%E5%B8%83
[mathjax-d]P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !}[/mathjax-d]标记为[mathjax]X \sim \pi(\lambda)[/mathjax]或者[mathjax]X\sim Pois(\lambda )[/mathjax] .
泊松分布的参数[mathjax]\lambda[/mathjax]是单位时间(或单位面积)内随机事件的平均发生率;[mathjax]E(x)=\lambda[/mathjax].
⚫️ 方差和期望
期望:[mathjax]E(X)[/mathjax],方差:[mathjax]D(X)[/mathjax] [mathjax-d]D(X)=E\left(X^{2}\right)-[E(X)]^{2}[/mathjax-d]
推导过程:
[mathjax-d]\begin{aligned} D(X) &=E[X-E(X)]^{2} \\ &=E\left[X^{2}-2 X \cdot E(X)+(E(X))^{2}\right] \\ &=E\left(X^{2}\right)-2 E(X) \cdot E(X)+[E(X)]^{2} \\ &=E\left(X^{2}\right)-[E(X)]^{2} \end{aligned}[/mathjax-d]给定均匀分布[mathjax]X \sim U[a,b][/mathjax],则
[mathjax]E(X)=\frac{b+a}{2}[/mathjax], [mathjax]D(X)=\frac{(b-a)^2}{12}[/mathjax].
推导:
[mathjax-d]E[\varphi(x)]=\int_{-\infty}^{\infty} \varphi(x) f(x) d x[/mathjax-d] [mathjax-d]\begin{aligned} E\left(x^{2}\right) &=\int_{a}^{b} x^{2} \frac{1}{b-a} d x \\ &=\frac{1}{3(b-a)}\left(b^{3}-a^{3}\right) \\ &=\frac{1}{3(b-a)}(b-a)\left(b^{2}+a b+a^{2}\right) \\ &=\frac{b^{2}+a b+a^{2}}{3} \end{aligned}[/mathjax-d] [mathjax-d]{[E(x)]^{2}=\left(\frac{a+b}{2}\right)^{2}} [/mathjax-d] [mathjax-d]\begin{aligned} D(x)=E\left(x^{2}\right)-[E(x)]^{2} &=\frac{b^{2}+a b+a^{2}}{3}-\left(\frac{a+b}{2}\right)^{2} \\ &=\frac{(b-a)^{2}}{12} \end{aligned}[/mathjax-d]⚫️ 矩估计/矩估计量
🔗 [矩估计 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/%E7%9F%A9%E4%BC%B0%E8%AE%A1
⚫️ 最大似然估计量
通过这些例题来复习:🔗 [参数估计之点估计(矩估计,最大似然估计) 详解+例题_Weary_PJ的博客-CSDN博客_求最大似然估计量例题] https://blog.csdn.net/Weary_PJ/article/details/106525960
▪ 重要例题(来自上面的链接):
设[mathjax]X \sim N\left(\mu, \sigma^{2}\right)[/mathjax] ; [mathjax] X_{1}, \cdots, X_{n}[/mathjax]是来自[mathjax]X[/mathjax]的一个样本,求参数[mathjax]\mu, \sigma^2[/mathjax]的最大似然估计量。
答案(如果推导生疏就去原链接看过程):
[mathjax-d]\left\{\begin{array}{l} \hat{\mu}=\frac{1}{n} \sum_{i=1}^{n} x_{i}=\bar{x} \\ \hat{\sigma^{2}}=\frac{\sum\limits_{i=1}^n \left(x_{i}-\bar{x}\right)^{2}}{n} \end{array}\right.[/mathjax-d]▪️ 另一个习题(比上面的简单一些):
答案:
[mathjax-d]\hat{\theta}=-\frac{\sum\limits_{i=1}^{n} \ln x_{i}}{n}[/mathjax-d]⚫️ 除法求导公式
[mathjax-d]\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-v^{\prime} u}{v^{2}}[/mathjax-d]⚫️ 重新回到最开始 I4dkEALQv34视频的MLE,现在这道题的解答就很容易得出了:
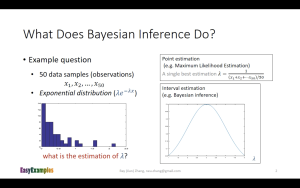
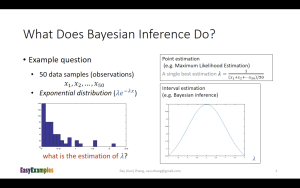
▪️ 设[mathjax]X[/mathjax]的概率密度为[mathjax]\lambda e^{-\lambda x}[/mathjax],[mathjax] X_{1}, \cdots, X_{n}[/mathjax]是来自[mathjax]X[/mathjax]的一个样本,求参数[mathjax]\lambda[/mathjax]的最大似然估计量。
过程:
[mathjax-d]\begin{gathered} L(\lambda)=\prod\limits_{i=1}^{n} f\left(x_{i}\right)=\lambda^{n} e^{-\lambda \sum\limits_{i=1}^{n} x_{i}} \\ \ln L(\lambda)=n \ln \lambda-\lambda \sum\limits_{i=1}^{n} x_{i} \\ \frac{\partial}{\alpha \lambda} l(\lambda)=\frac{n}{\lambda}-\sum\limits_{i=1}^{n} x_{i}=0 \\ \hat{\lambda}=\frac{n}{\sum\limits_{i=1}^{n} x_{i}}=\frac{1}{\bar{x}} \end{gathered}[/mathjax-d]⚫️ 在之前的视频(https://www.youtube.com/watch?v=5NMxiOGL39M)里,作者用他的狗举了一个例子:
[mathjax-d]\displaylines{p(w|m)=\frac{p(m|w)\cdot p(w)}{p(m)} \cr p(w|m)\propto p(m|w)\cdot p(w) \cr w: \text{weight, } m: \text{measure of weight}}[/mathjax-d]如果把先验概率[mathjax]p(w)[/mathjax]视为均匀分布,那么上式就可以写为:
[mathjax-d]p(w|m)\propto p\left(m=m_{1} \mid w=w_{0}\right) * p\left(m=m_{2} | w=w_{0}\right) * \cdots * p\left(m=m_{n} \mid w=w_{0}\right)[/mathjax-d]看起来和[mathjax]L(\lambda)=\prod\limits_{i=1}^{n} f(x_{i})[/mathjax]的形式有些类似,事实上,[mathjax]p(w)[/mathjax]为均匀分布的时候这个例子变成了上文提到的习题“求参数xxx的最大似然估计量”,MLE和MAP之间建立了联系。
From the point of view of Bayesian inference, MLE is a special case of maximum a posteriori estimation (MAP) that assumes a uniform prior distribution of the parameters.
https://stats.stackexchange.com/a/329553
同时,在2022-08-20的笔记里补充了一张图片:
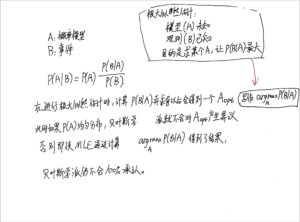
本笔记后面的这张2图片也对这个性质进行了补充。
⚫️ 视频https://www.youtube.com/watch?v=I4dkEALQv34的bayesian inference步骤:
注:
这里第一张图的MLE的解法步骤写在本笔记前面。
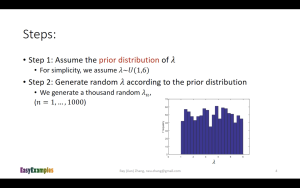
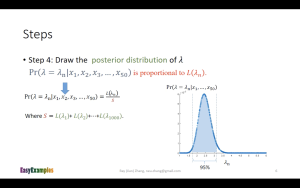
对下面的slide进行一点推导注解:


这个slide在进行bayesian inference的时候,对prior生成的是uniform distribution数据,也就是说这个slide所做的内容仍然是MLE,只是换了一种方法来进行:一种方便计算机编程计算的方法。这样可以避免进行公式推导(缺点就是单纯用计算机很难搞出解析解)。
一个类似的场景是用计算机求一元三次方程的近似解。在大致确定定义域后,直接对定义域里的每一个可能的取值进行计算,直到找出那个/那些 近似解为止。比如要从0~10里面找出近似解:把0, 0.000001, 0.000002, 0.000003, .... 9.999998, 9.999999, 10 丢进去计算。
Bayesian Inference的python demo
代码和运行结果
用代码复现上面的一系列步骤
import math
import random
import matplotlib.pyplot as plt
import numpy as np
real_lambda = 3
print("real lambda: " + str(real_lambda))
x = np.random.exponential(scale=1 / real_lambda, size=50)
# plt.figure()
# plt.hist(x)
# plt.show()
MLE = 1 / (sum(x) / len(x))
print("lambda using MLE: " + str(MLE))
guess_lambda = []
L_lambda = []
posterior = []
for i in range(0, 1000):
guess_lambda.append(random.uniform(0.0, 6.0))
for lambda_n in guess_lambda:
L_lambda_n = lambda_n * (math.e ** ((-1) * lambda_n * x[0]))
for i in range(1, len(x)):
L_lambda_n *= lambda_n * (math.e ** ((-1) * lambda_n * x[i]))
L_lambda.append(L_lambda_n)
L_lambda_sum = sum(L_lambda)
for item in L_lambda:
posterior.append(item / L_lambda_sum)
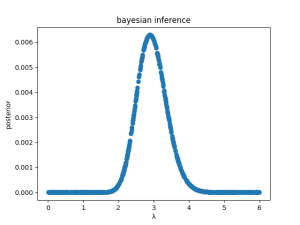
plt.figure()
x_axis = [guess for guess in guess_lambda]
plt.scatter(x_axis, posterior)
plt.title("bayesian inference")
plt.xlabel('λ')
plt.ylabel('posterior')
# plt.show()
plt.savefig('bayesian_inference.png')
print("max lambda in posterior: " + str(guess_lambda[np.argmax(posterior)]))
结果:
real lambda: 3
lambda using MLE: 2.892228772723222
max lambda in posterior: 2.893595478188743如果反复运行多次,会发现:
1,程序存在一定误差(在上述程序的参数下,误差普遍0.1~0.5之间);2,尽管有的时候程序猜测[mathjax]\lambda[/mathjax]的值有一定偏差,但使用点估计-MLE直接计算的[mathjax]\lambda[/mathjax],和使用bayesian inference直接计算的[mathjax]\lambda[/mathjax],是近似相等的。
❓ 仍然具有一定偏差(无论是猜测[mathjax]\lambda[/mathjax]与真实[mathjax]\lambda[/mathjax]之间的偏差,还是两种方法计算[mathjax]\lambda[/mathjax]得到结果的略微不一致)的主要原因:大概是因为使用 random.uniform() 得到的数据不够uniform(可以通过增大 len(guess_lambda) 来减小误差);同时, x 使用大量散点替代真实曲线,也具有一些误差(可以通过增大 len(x) 来减小误差)。
如何生成prior distribution data?
那如果我给prior设定一个比较复杂的概率分布函数(而不是像上面python程序那样使用Uniform Distribution),怎么生成这些数据?
这类问题统称 sampling ,比如Monte Carlo抽样 / 蒙特卡洛抽样。