This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
为什么会有这篇笔记？
本笔记写于2023年8月，原因是发现自己时隔一年无法盲背prior/posterior/MLE/MAP的一些概念，尤其是MLE和MAP.
所以本笔记不怎么涉及贝叶斯网络/贝叶斯滤波/卡尔曼滤波 等内容，能重新学会就可以，并不一定需要把所有的笔记列举完毕，因为过去2年写的笔记里和条件概率挂钩的东西有点多，各个角落里都有。更新：甚至不需要专门做一个笔记整理集合。
下面是从零开始回顾这些概念的学习笔记：
最开始根据惯性记忆写出了这个公式：
[mathjax-d]P(A \mid B)=\frac{P(B \mid A) \cdot P(A)}{P(B)}[/mathjax-d]知道[mathjax]P(A \mid B)[/mathjax]是posterior，[mathjax]P(A)[/mathjax]是prior，然后剩下的就记不得了，尤其是对[mathjax]P(B \mid A)[/mathjax]和[mathjax]P(B)[/mathjax]解释不清。所以本篇笔记也就是从这里开始的。
重新理解Likelihood，MLE，MAP等概念
[mathjax-d]P(A \mid B)=\frac{P(B \mid A) \cdot P(A)}{P(B)}[/mathjax-d]通过复习现在知道了[mathjax]P(B \mid A)[/mathjax]是"Likelihood", [mathjax]P(B)[/mathjax]是"Evidence"，接下来要完全理解这些概念：
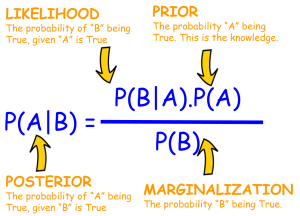
现在一个关键的问题在于如何重新理解Likelihood
先搜集一些wikipedia的严谨定义：
The likelihood function (often simply called the likelihood) is the joint probability of observed data viewed as a function of the parameters of a statistical model.
https://en.wikipedia.org/wiki/Likelihood_function
好了，现在开始解释：
一枚正反面均匀的硬币随机扔50次，你认为扔出“正面25，反面25”的可能性有多大？可以用[mathjax]{{50}\choose{25}}(0.5)^{25}(0.5)^{25}[/mathjax]计算出这个概率，得到的结果就是likelihood.
那么，MLE - maximum Likelihood呢？当然就是 argmax(模型） ，也就是说“当这个概率模型长什么样的时候，它最有可能生成这些数据“。
比如硬币的问题：
一个硬币扔了10000次，其中5000次正面，5000次反面，那么我认为它最有可能是什么样子的硬币？我当然会认为它最有可能是一枚正反面均匀的硬币。
那么，MAP - maximize a posteriori（或者写成maximum a posteriori）呢？其实同样是对 模型 的估量（推测这个模型最有可能长什么样），只不过MAP属于贝叶斯学派，他们会先天的给这个模型添加一个prior作为“偏见”，仅此而已！
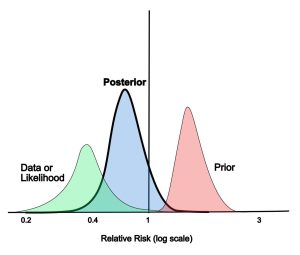
所以回到贝叶斯的公式：
[mathjax-d]P(A \mid B)=\frac{{\color{red}P(B \mid A)} \cdot P(A)}{P(B)}[/mathjax-d]整个公式是属于MAP的，而MLE只关心[mathjax]\color{red}P(B \mid A)[/mathjax]这一个东西而已！
接下来会继续建立MLE和MAP的联系：
前面学习MLE的时候已经知道了，MLE的本质就是argmax(模型)，那么具体是怎么做的呢？
当然我们学过点估计/矩估计这些：🔗 [2022-08-20 - Truxton's blog] https://truxton2blog.com/2022-08-20/
也学过贝叶斯估计：🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
在此之前同时了解一下 频率学派（Frequentist inference）/点估计/MLE/贝叶斯学派（Bayesian inference）/MAP/...的关系：
（作为标注，下面的图中有一些链接的字体颜色不太一样）
MLE和MAP之间的联系
uniform distribution prior（先验均匀分布）
接下来讨论MLE和MAP之间产生联系的条件：
- prior: uniform distribution，此时MLE=MAP
- observe data -> [mathjax]\infty[/mathjax]
先讨论第1个（prior: uniform distribution），这个东西其实在🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/ 就已经有过相关笔记：
在🔗 [2022-08-20 - Truxton's blog] https://truxton2blog.com/2022-08-20/ 也有提到：
观测数据趋于无限
再来讨论第2个：observe data -> [mathjax]\infty[/mathjax]
严谨的证明暂时不会，相关讨论可以后续有机会看：🔗 [Maximum likelihood equivalent to maximum a posterior estimation - Cross Validated] https://stats.stackexchange.com/questions/52395/maximum-likelihood-equivalent-to-maximum-a-posterior-estimation
先想象一些东西：
相比于政府发行的巨量硬币（正常硬币），地球上很难找到一枚明显正反面不均匀的硬币，所以贝叶斯学派有了一个相当强硬的prior，认为P（硬币随机扔出正面）= 0.5 . 但现在我们给贝叶斯学派送出了一组观测数据，
数据结果表明：扔了10次，4次正面，此时贝叶斯学派认为这只是观测数据太少，这枚硬币大概率还是正反面均匀的。
又来了一组数据：扔了100次，40次正面，此时贝叶斯学派的计算结果会继续靠近0.4（认为这枚硬币确实大概率是正反面不均匀的）
又来了一组数据：扔了100000次，40000次正面，此时贝叶斯学派的计算结果会非常非常靠近0.4
又来了一组数据：扔了10000000次，4000000次正面，此时贝叶斯学派的计算结果会非常非常非常靠近0.4
....
写个程序模拟一下这个硬币实验，其中贝叶斯学派的人认为硬币投出正面的prior是[mathjax]\mu=0.5[/mathjax]的正态分布
假设投出了这些结果：
5次-2正
10次-4正
50次-20正
500次-200正
代码是草稿，注意有很多问题：
- 生成normal distribution prior的代码是chatgpt写的，暂时懒得改进了（调了好几次才调好，最后用的还是我的思路，chatgpt似乎变笨了）
- 就算是调好的chatgpt代码仍然一堆问题：2024-02-14我又发现了2个问题，并整理了一篇笔记：🔗 [2024-02-14 有关numpy整数处理的一些问题 - Truxton's blog] https://truxton2blog.com/2024-02-14-numpy-integer-handling-issue/
- 画图看个大概就行，坐标轴没有调的
from math import comb
import matplotlib.pyplot as plt
import numpy as np
import random
result_group = []
for total in (5, 10, 50, 500):
prob = []
for p in np.arange(0, 1.01, 0.01):
front = int(total * 0.4)
back = total - front
prob.append(comb(total, front) * np.power(p, front) * np.power((1 - p), back))
result_group.append(prob)
plt.figure()
plt.plot(result_group[0], color="black", label="5")
plt.plot(result_group[1], color="green", label="10")
plt.plot(result_group[2], color="blue", label="50")
plt.plot(result_group[3], color="red", label="500")
plt.legend()
plt.savefig('MLE.png')
########################################################
# begin stupid chatgpt code
# 2024-02-14 我发现原本代码里的np.clip()有问题，进行了修改，同时增大了num_values，目的是让prior更精确
# 2024-02-14 我发现原本代码里的np.random.normal(mean, std_deviation, num_values).astype(int)有问题，会导致生成的0比1多（因为-0.x也被算成了0）
mean = 50
std_deviation = 15
num_values = 100000000
raw_integer_values = np.rint(np.random.normal(mean, std_deviation, num_values)).astype(int)
filtered_integer_values = raw_integer_values[(raw_integer_values >= 0) & (raw_integer_values <= 100)]
# Count the occurrences of each integer value
counter = np.bincount(filtered_integer_values, minlength=101)
# Normalize the counter array to get probabilities
probabilities = counter / np.sum(counter)
# Generate x values for the scatter plot (integer values)
x_values = np.arange(0, 101)
# Create a scatter plot
plt.figure()
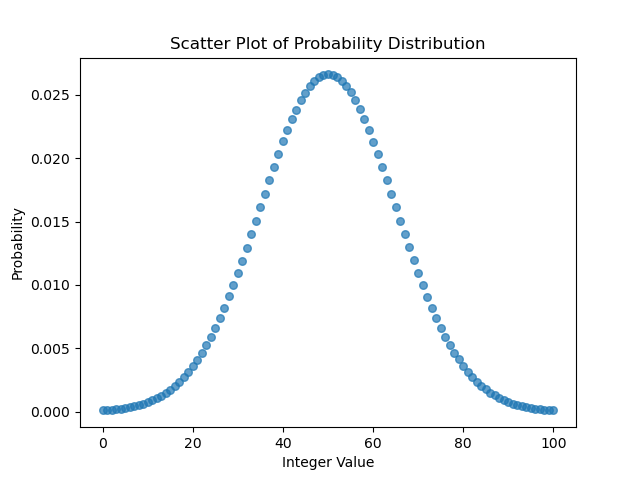
plt.scatter(x_values, probabilities, marker='o', s=30, alpha=0.7)
plt.xlabel("Integer Value")
plt.ylabel("Probability")
plt.title("Scatter Plot of Probability Distribution")
plt.savefig('prior.png')
# end stupid chatgpt code
########################################################
posterior_group = []
for group in result_group:
if (len(group) != len(probabilities)):
print('check your code')
exit(1)
temp = []
for i in range(0, len(group)):
temp.append(group[i] * probabilities[i])
posterior_group.append(temp)
plt.figure()
plt.plot(posterior_group[0], color="black", label="5")
plt.plot(posterior_group[1], color="green", label="10")
plt.plot(posterior_group[2], color="blue", label="50")
plt.plot(posterior_group[3], color="red", label="500")
plt.legend()
plt.savefig('MAP.png')
结果：
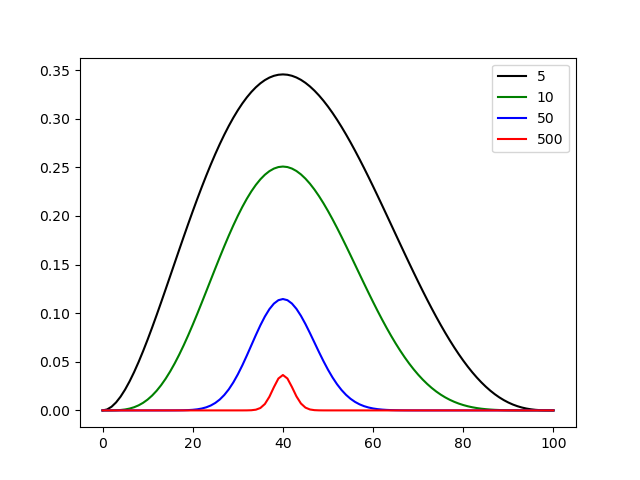
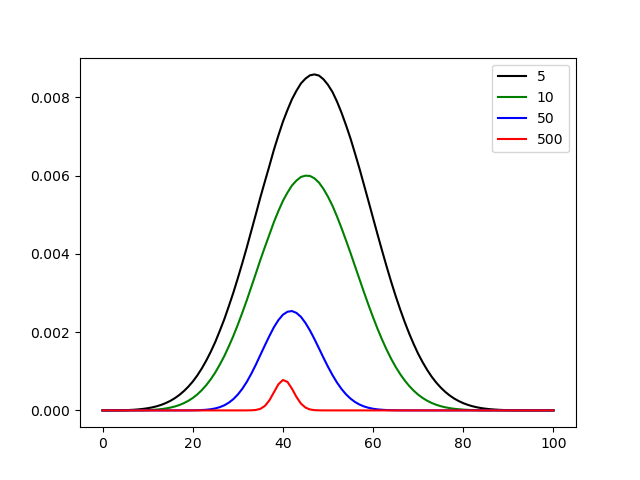
从MAP.png可以看出，随着数据的不断增多，贝叶斯学派对这枚硬币的看法会不断接近40（代表P=0.4，懒得改坐标轴代码了）
注意，MLE和MAP的纵坐标放在一起对比没什么意义，对模型的估计要的是argmax(模型)，也就是说模型分布的中心趋向于哪里就估计哪里。
