This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
参数估计与抽样方法
与另一篇笔记的关系
今天的笔记比较混沌，总结来说就是：
尝试学习（以前稍微学过一点的） 马尔可夫链蒙特卡洛算法 mcmc ，结果发现 点估计/矩估计/最大似然估计量/… 的内容更重要，所以重新学习这部分内容，并对以前的笔记（2021-10-22）进行了补充（主要是公式的推导）。
所以如果要复习 点估计/矩估计/最大似然估计量/… ，应该同时看这篇笔记和2021-10-22的笔记。
如果要复习 贝叶斯推断/Bayesian inference ，应该看2021-10-22的笔记。
截止到2022-12-08， 马尔可夫链蒙特卡洛算法 mcmc 暂时还没有在任何笔记里进行过详细的学习和推导。
今天从哪里开始？
整合笔记：p=8159
马尔可夫链蒙特卡洛算法 mcmc
先尝试搜索以前的笔记吧，我记得以前学过这个的：
🔗 [2021-12-03 - Truxton's blog] https://truxton2blog.com/2021-12-03/
同时有另一个相关性较强的概念：最大似然估计量 🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
学了跟没学一样，重新学吧：
🔗 [MCMC 蒙特卡罗马尔科夫算法 Metropolis–Hastings + Gibbs 采样 | Echo Blog] https://houbb.github.io/2020/01/28/math-05-mcmc
下面就是最核心的内容：MCMC到底用来做什么？
停！先去修这篇文章好了：🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
准备处理未完成的笔记：MCMC
p=8159
但是发现 点估计/矩估计/最大似然估计量/... 的内容更重要，翻出以前的老笔记：
preview1 preview2 preview3🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
先写在这里吧，写完了再决定要不要合并到2021-10-22的老笔记中。
参数估计、点估计、最大似然估计、极大似然估计、矩阵估量、矩估量…的关系
参数估计、点估计、最大似然估计、极大似然估计、矩阵估量、矩估量...的关系（这部分内容是不是应该移到前面？）
总结：（尽量使用通俗但不严谨的思路去理解）
点估计就是用观测的样本强行估计概率模型，里面包括 矩估计 和 最大似然估计量 .
矩估计就是用样本矩（[mathjax]E(X), E(X^2)...[/mathjax]）这些东西来估计概率模型。
最大似然估计（量）就是找出一个模型，恰好使得这个模型产出这些观测数据的可能性最大。比如我有观测数据：（硬币）5000正5000反，我肯定会从一堆歪瓜裂枣的不均匀硬币里挑出那个正反面均匀的硬币作为我们想要的模型。
接上面的硬币案例，如果我们生活在一个奇特的世界，90%的硬币都是非常不均匀的，而我们恰好有一个硬币，它产生了一组（正面投掷计数=反面投掷计数）的观测数据，那么即使通过最大似然估计量算出了硬币的模型（正反均匀），贝叶斯学派也不会100%承认/信任我们的结果。
点估计、矩估计、最大似然估计的一些例题推导
点估计
先学习矩估计：
首先明确一个重要概念：
样本矩：
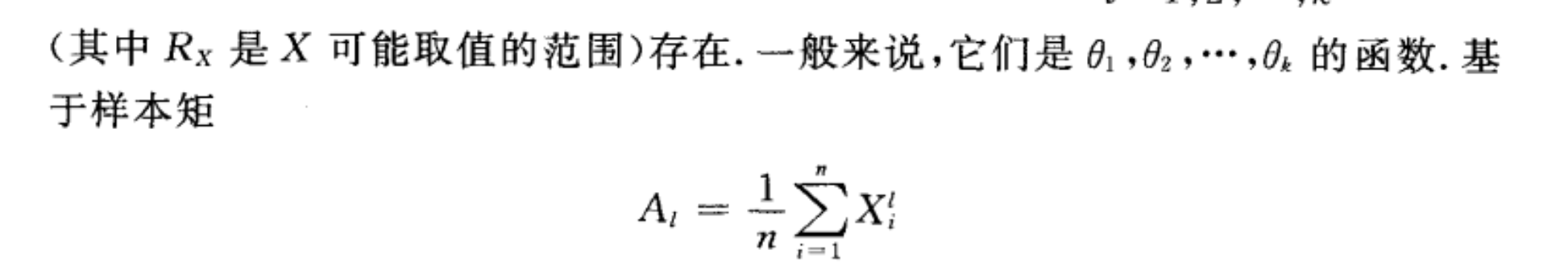
还是从这里开始：
也就是：
可以简单理解为：用观测推测概率模型。
比如我得知一个硬币抛了1000000次，有499999次正面和500001次反面，那么我可以估计这个硬币是正反面均匀的。P（正面）=1/2，P（反面）=1/2 .
矩估计：均匀分布
下面的笔记和以下内容有关：
均匀分布，均匀分布的期望，均匀分布的[mathjax]E(x^2)[/mathjax]，均匀分布的方差
且均和2021-10-22的笔记以及这个CSDN博客的内容有关，下面的内容在2021-10-22的笔记里已经有了，只是今天选择再做一遍。
求[mathjax]E(x^2)[/mathjax]的资料可以参考：🔗 [Expectations] https://www3.nd.edu/~rwilliam/stats1/x12.pdf
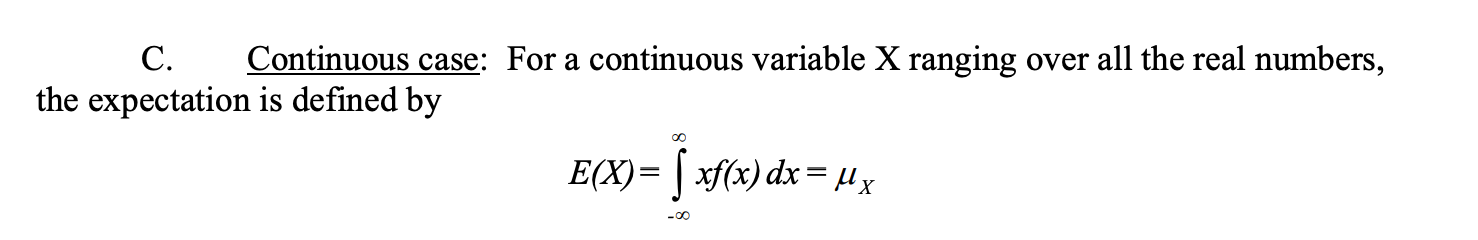
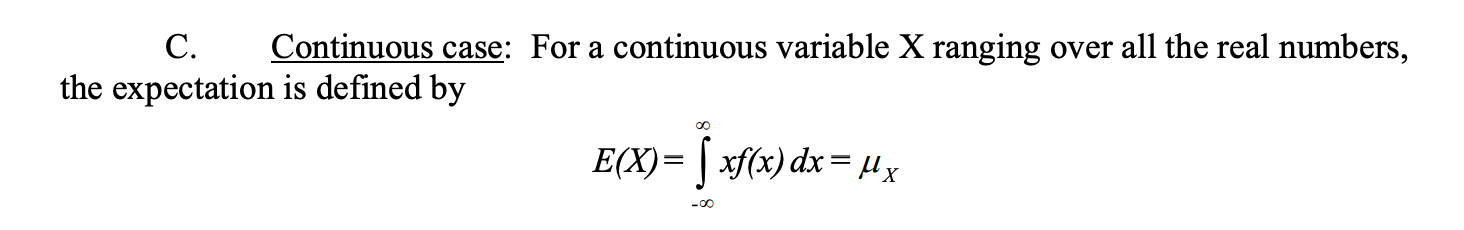
接下来是推导笔记：
在完成了上面的「均匀分布矩估计」以后，这道题应该是可以直接做出来的：
最大似然估计量
先列举一些基本例题，在这些例题里得到的结果和 矩估计量 的结果是相同的。
来自浙大概率论P153~P155
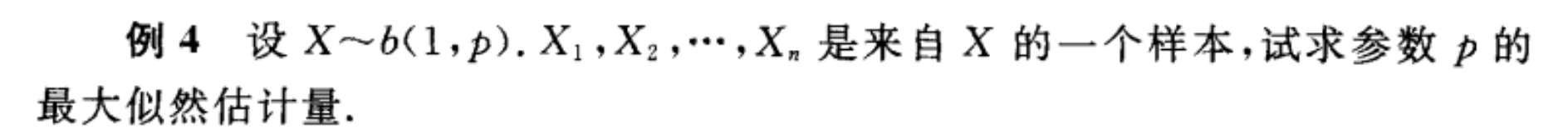
以及：
接下来是 最大似然估计量 和 矩估计量 结果不同的情况：
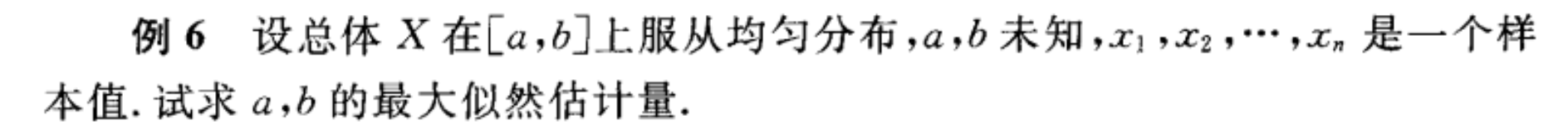
答案：
注意到红框里的内容，可以这么理解：最大似然估计参数[mathjax]a[/mathjax]和[mathjax]b[/mathjax]，首先一定要满足的条件是「估计出来的概率模型能够产生出这些观测数据（概率不能为0）」。所以[mathjax]a\leq \text{min}(\text{X series})[/mathjax]和[mathjax]b\geq \text{min}(\text{X series})[/mathjax]是必须的，否则产生[mathjax]x_1\sim x_n[/mathjax]的概率肯定为0 .
基本例题都做完了，先学到这里，然后回看一遍 🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/
还发现了一道例题：
以及一个补充结论：
对上面补充结论的笔记：
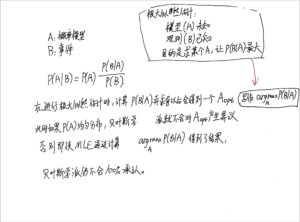
Bayesian Inference和抽样方法建立联系
接这里：
从这个例子接着往下想就到了bayesian inference的领域：
preview 直接去看2021-10-22的笔记就可以！
但是2021-10-22的笔记里面的例子使用的是Prior ~ Uniform distribution，也就是说，可以很容易用各类编程语言里的random()/randomInt()来生成。
那如果我给prior设定一个比较复杂的概率分布函数，怎么生成这些数据？
这类问题统称 sampling ，比如Monte Carlo抽样/蒙特卡洛抽样，Gibbs sampling，接受-拒绝采样。
如果不准备继续深入推导Monte Carlo，那么这一块的内容就暂时学到这里。
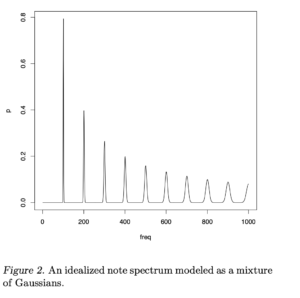
弦乐器频谱采集符合GMM模型吗？
（合并笔记，p=8197）弦乐器频谱采集符合GMM模型吗？
目前认为是符合GMM模型的，因为：采集声音无法避免噪声，而噪声可以认为是Gaussian，再加上harmonic series，总体就可以认定为GMM模型。
从这里开始：
