再次理解线性回归中的p-value
有老笔记🔗 [2021-09-21 - Truxton's blog] https://truxton2blog.com/2021-09-21/ 里面提到的链接:https://www.zhihu.com/question/23149768/answer/282842210
简单来说p-value就是“出意外的概率”.
p-value越小越好,越小的p-value代表“发生意外的概率越低”,也代表预测的结果越可信(意外=发生了预测结果之外的事情=预测失败)。

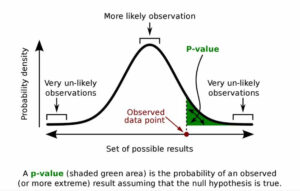
接下来就是linear regression中各个变量的p-value代表什么,”意外“代表什么
答案:”发生意外“代表[mathjax]H_0[/mathjax]:这个变量(predictor)的系数(coefficient)为0 . coef为0就代表这个变量在模型里不起任何作用。
所以一个很小的p-value的意思就是“这个变量经过预测,它现有的coef为xxx(反正不是0),而且这个变量的coef为0的概率极低(0.00001),所以这个变量在模型里应该是很有作用的“。
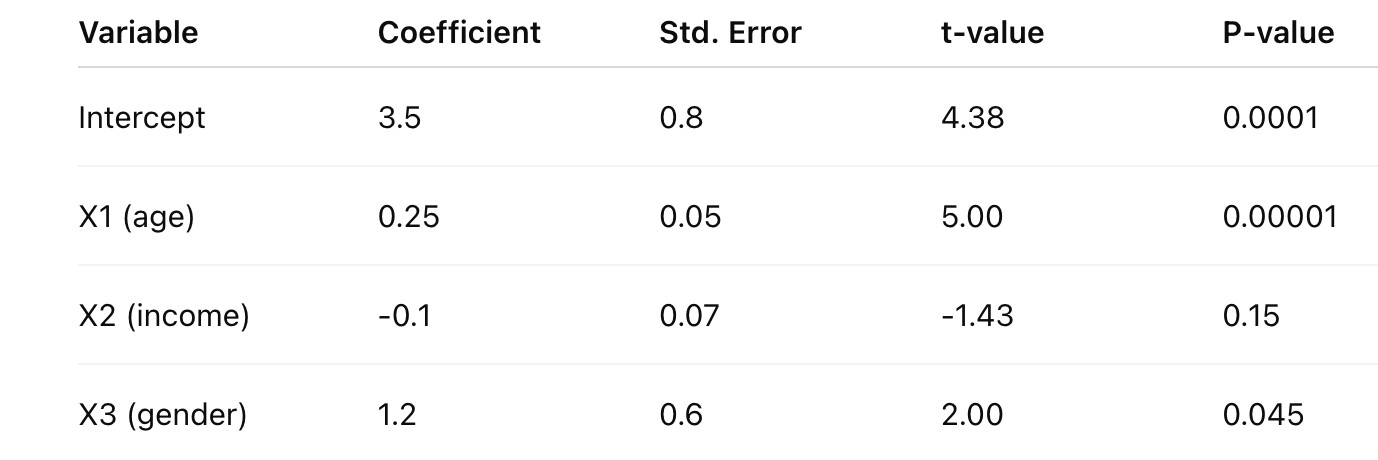
以上面的图的x1(age)为例,解释为:当前模型里我们认为它的系数为0.25,我们有很大把握这么说,因为发生意外(age的coef实际为0)的概率很低,为0.00001.
在linear regression流程中,t-value比p-value更早计算出来
t-value一般认为越大越好,比2大的可以认为是strong,所以上面的表中
x1(age)有大的t-value和小的p-value,这个predictor作用很大
x2(income)有负的t-value和大的p-value,这个predictor不是很可靠也没啥作用
x3(gender)还行,比较有用
再来学点p-value的计算过程,因为理解p-value的时候经常搞不清楚p-value和[mathjax]\mathcal{N} (\mu, \sigma^2)[/mathjax]的2个参数[mathjax]\mu, \sigma^2[/mathjax]之间有什么先后顺序的关联。(比如:是不是越肥的钟型曲线p-value就一定越低?)
看了一圈还是要从中心极限定理开始(已经搜过了在2025-06-21之前基本没有详细的相关笔记,基本上都是一笔带过)
中心极限定理
现在有一个0~10之间产生随机数(均匀分布)的机器,它产生了1000组数据,这1000组数之和大概是什么样子?
--- 近似于正态分布
现在有一个产生0或者10的机器(50%产生0,50%产生10),它产生了1000组数据,这1000组数之和大概是什么样子?
--- 近似于正态分布
现在有一个产生0或者10的机器(99%产生0,1%产生10),它产生了1000组数据,这1000组数之和大概是什么样子?
--- 近似于正态分布
(等等)
等于是说(排除一些平均数无限大方差无限大的特殊分布)绝大部分情况下能想到的各种分布产生的一堆数字,这些数字的和(sum)以及平均数都近似于一个正态分布。
(浙大概率论P122,第一张图片对应数字之和,第二张图对应数字的平均数)


代码验证:
例题
下面这道例题被区分为“第一种例题”因为它是用的是Z-test (z-test 和 t-test的区间见这道题之后的笔记)
浙大概率论P124

答案

解题步骤里的[mathjax]D(V_k)=100/12[/mathjax]来自均匀分布方差的计算,在以前的笔记里面有:🔗 [2021-10-22 - Truxton's blog] https://truxton2blog.com/2021-10-22/

核心步骤:
[mathjax-d]\frac{\bar{X}-\mu}{\phi/{\sqrt{n}}}=\frac{\bar{X}-5}{\frac{\sqrt{\frac{100}{12}}}{\sqrt{20}}}\sim\mathcal{N}(0, 1)[/mathjax-d]其中[mathjax]\bar{X}[/mathjax]本身遵循另一个正态分布,上面的公式只是把它规范成了[mathjax]\mathcal{N}(0, 1)[/mathjax]方便计算。
题目询问的是[mathjax]P(\sum{X}>105)[/mathjax]或者说[mathjax]P(\bar{X}>\frac{105}{20})[/mathjax],所以只需要求出正态分布[mathjax]\frac{\bar{X}-5}{\frac{\sqrt{\frac{100}{12}}}{\sqrt{20}}}[/mathjax]在[mathjax]x=105/20[/mathjax]这条线右侧的面积即可。
由于上面的这个正态分布本质上就是[mathjax]\mathcal{N}(0, 1)[/mathjax],所以最终只需要查表[mathjax]\phi(0.387)[/mathjax]即可
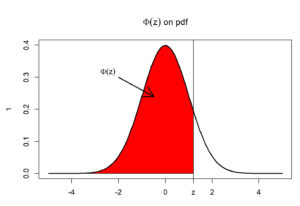
上面的例题还没有用到p-value,所以再补充一个带p-value的题目(本质上其实是一样的,都是中心极限定理的应用)
但首先要特别注意z-test(用于上面的例题)和t-test(用于下面的例题)的细微区别:


在上面的例题1(噪声电压)里,整个群体(数量无限多的噪声电压采样)的均值/方差/标准差我们是知道的,所以我们选用z-test
但如果是下面这道例题(这道例题已经出现在了🔗 [2024-09-15 概率论学习(假设检验) - Truxton's blog] https://truxton2blog.com/?p=15209)

这里只能计算出16个抽样元件的均值/方差/标准差,所以需要用t-test
另外要注意计算方差的时候使用的是n-1,对应np.std里面的ddof=1

这道题有t-value检验法和p-value检验法,先粘贴p216的p-value解答:

这里面的最后一步不是[mathjax]\phi(x)[/mathjax]的计算方法,而是需要加入df (degree of freedom)的计算方法(同时,因为这是单边问题,所以还要选上one-tailed):
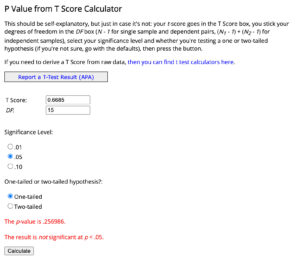
也附带上p184的t-value检验法(大部分过程是一样的,只是这里计算了[mathjax]t_{0.05}(15)[/mathjax]):
