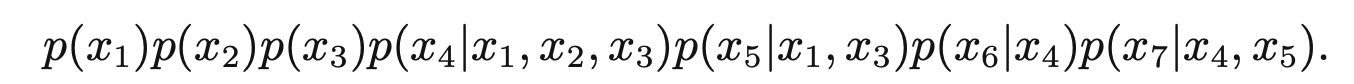This post was published in 2022-08-02. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
本篇笔记的主要内容
(本笔记的曾用标题为「贝叶斯网络在MIR领域的应用」)
本篇笔记主要是PRML第8章 graphics model的入门部分,包括:概率论复习,一些基本概率论公式,图模型,D-separation的推导,markov blanket,有向图variable elimination,HMM variable elimination(也就是forward+backward algorithm的基础)
概率论基础知识
阅读这篇文章的时候突然想到的这个话题。
首先还是要复习一下贝叶斯基本定理:
首先是条件概率公式:
[mathjax-d]P(A \mid B)=\frac{P(A, B)}{P(B)}[/mathjax-d]然后是贝叶斯定理:
[mathjax-d]P(A \mid B)=\frac{P(B \mid A) \cdot P(A)}{P(B)}[/mathjax-d]写成这种形式在某些时候可能会有用:
[mathjax-d]P(A \mid B)=\frac{P(A)}{P(B)} P(B \mid A)[/mathjax-d]翻出之前的老笔记(补充了一点新内容):preview 🔗 [2021-12-13 - Truxton's blog] https://truxton2blog.com/2021-12-13/#贝叶斯定理又忘了
全概率公式:
🔗 [贝叶斯公式学习笔记 | Leo的博客] https://leehao.me/贝叶斯公式学习笔记/
[mathjax-d]P(A)=P\left(A \mid B_{1}\right) P\left(B_{1}\right)+P\left(A \mid B_{2}\right) P\left(B_{2}\right)+\ldots+P\left(A \mid B_{n}\right) P\left(B_{n}\right)[/mathjax-d]或者简单写为:
[mathjax-d]P(A)=\sum_{B}P(A\mid B)P(B)[/mathjax-d]由此可以推导更一般情况下的贝叶斯公式(把贝叶斯公式的分母替换成全概率公式即可):
[mathjax-d]P\left(A_{i} \mid B\right)=\frac{P\left(B \mid A_{i}\right) P\left(A_{i}\right)}{\sum_{j} P\left(B \mid A_{j}\right) P\left(A_{j}\right)}[/mathjax-d]链式法则-chain rule
🔗 [Chain rule (probability) - Wikipedia] https://en.wikipedia.org/wiki/Chain_rule_(probability)
n=2的最原始公式肯定是知道的:
[mathjax-d]\mathrm{P}(X, Y)=\mathrm{P}(X \mid Y) \cdot P(Y)[/mathjax-d]通过这个n=4的例子来记住一般规律:
[mathjax-d]\begin{aligned} \mathrm{P}\left(X_{4}, X_{3}, X_{2}, X_{1}\right) &=\mathrm{P}\left(X_{4} \mid X_{3}, X_{2}, X_{1}\right) \cdot \mathrm{P}\left(X_{3}, X_{2}, X_{1}\right) \\ &=\mathrm{P}\left(X_{4} \mid X_{3}, X_{2}, X_{1}\right) \cdot \mathrm{P}\left(X_{3} \mid X_{2}, X_{1}\right) \cdot \mathrm{P}\left(X_{2}, X_{1}\right) \\ &=\mathrm{P}\left(X_{4} \mid X_{3}, X_{2}, X_{1}\right) \cdot \mathrm{P}\left(X_{3} \mid X_{2}, X_{1}\right) \cdot \mathrm{P}\left(X_{2} \mid X_{1}\right) \cdot \mathrm{P}\left(X_{1}\right) \end{aligned}[/mathjax-d]或者使用这个更一般的公式:
[mathjax-d]\begin{aligned} P\left(X_{1}, \ldots, X_{n}\right) &=P\left(X_{1}\right) P\left(X_{2} \mid X_{1}\right) \cdots P\left(X_{n} \mid X_{1}, X_{2}, \ldots, X_{n-1}\right) \\ &=\Pi_{i=1}^{n} P\left(X_{i} \mid X_{1}, X_{2}, \ldots, X_{i-1}\right) \end{aligned}[/mathjax-d]判断是否条件独立
如果:
[mathjax-d]P(A,B \mid C)=P(A \mid C)\cdot P(B \mid C)[/mathjax-d]那么A和B在给定条件C时条件独立。
额外补充一个经常使用的公式
补充一个经常用到的公式,熟练掌握可以快速解决很多推导过程:
[mathjax-d]P(A, B \mid C)=P(A \mid B, C)*P(B\mid C)[/mathjax-d]变体:
[mathjax-d]\sum_B\left[ P(A \mid B, C)*P(B\mid C)\right]=\sum_B P(A, B \mid C)=P(A \mid C)[/mathjax-d]边缘概率/概率的积分计算
边缘概率/概率的积分计算
在进行贝叶斯网络相关性推导的时候经常用到类似公式;此外,variable elimination的第一步就会用到这个:
[mathjax-d]P(A, B)=\sum_{c} P(A, B, C)[/mathjax-d]当然,添加多少变量都可以:
[mathjax-d]\begin{aligned} P(X) &=\sum_{U} \sum_{V} \sum_{W} \sum_{Y} \sum_{Z} P(U, V, W, X, Y, Z) \\ &=\sum_{U, V, W, Y, Z} P(U, V, W, X, Y, Z) \end{aligned}[/mathjax-d]特别注意
在PRML的8.30和8.31会遇到类似这样的积分公式:
[mathjax-d]P(G)=\sum_{B} \sum_{F} P(G \mid B, F) \cdot P(B) \cdot P(F) [/mathjax-d]以及
[mathjax-d]P(G \mid F)=\sum_{B} P(G \mid B, F) \cdot P(B)[/mathjax-d]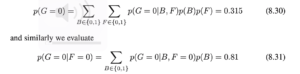
要注意这个公式是有前提条件的:head-to-head模型
此外,在HMM模型里也会遇到一个诡异的公式:
(https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture4.pdf)
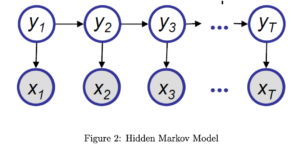
或者写成这样会更容易理解一些:
[mathjax-d]P\left(y_{i} \mid x_{1}, \ldots, x_{T}\right) \propto \sum_{y_{1}} \sum_{y_{2}} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_{T}} P\left(x_{1}, x_{2} \cdots x_{T}, y_{1}, y_{2} \cdots y_{T}\right) [/mathjax-d]过渡内容
下面的内容为过渡笔记:
贝叶斯网络
写在最前面:在本篇笔记中,贝叶斯网络的最大作用就是「简化复杂的全概率公式」.
复习一下最基本的贝叶斯网络
之前有笔记,但全都是粘贴链接:preview 🔗 [2021-11-20 - Truxton's blog] https://truxton2blog.com/2021-11-20/
重新学习贝叶斯网络的推导
重新学习贝叶斯网络的推导
从PRML p360 GRAPHICAL MODELS开始
学会理解贝叶斯网络的图模型:
写出下面graph的7个变量的联合概率

随后跳过一些内容,来到8.2 Conditional Independence
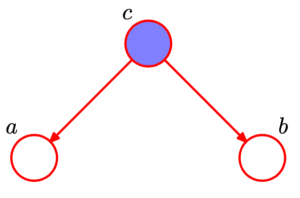
Three example graphs
写在前面:接下来的一些内容主要是围绕下面以下3种基本的图模型进行推导:
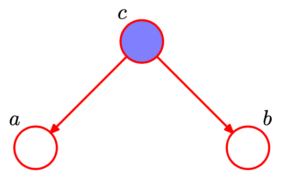
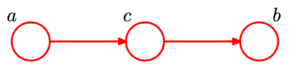
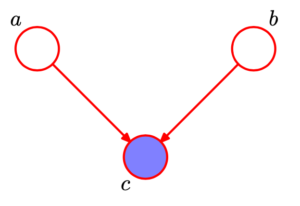
对每一种情况,都需要推导/证明以下内容:
1,如果什么都没有观测到(no observation),那么a和b是否条件独立?
2,在观测到c的情况下,a和b是否条件独立?
一般证明方法:

preview 8.2一开始有一个简单的条件概率推导:
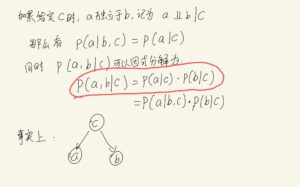
对这一步分内容的笔记:
tail-to-tail
情况1:tail-to-tail


head-to-tail
接下来是另一种情况:

然而在推导公式8.26的时候遇到了问题:
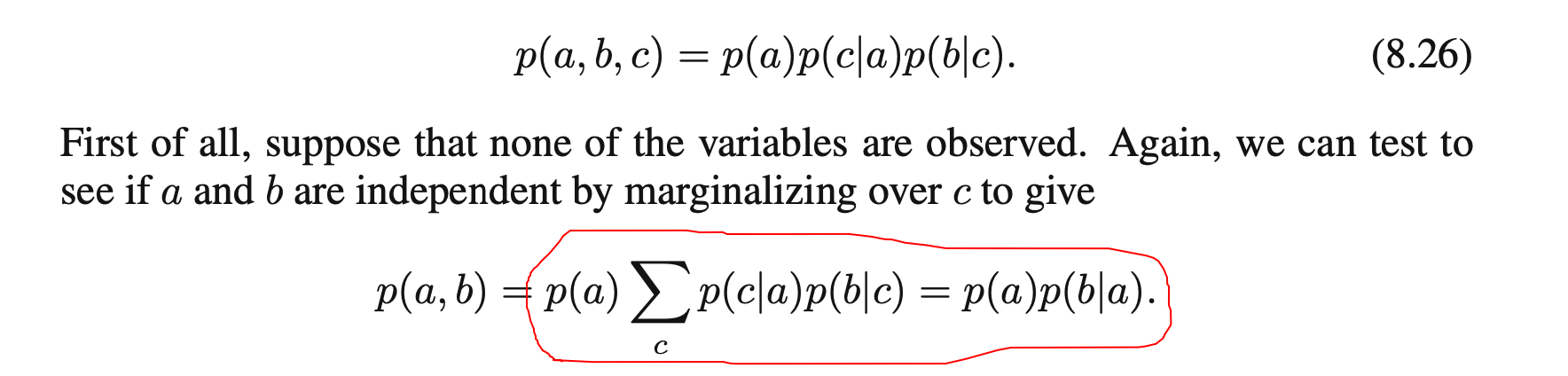
红圈里的这一步如何证明?
一开始完全想不通,后来在网上搜到了回答:(具体证明过程不用看,貌似2个字母写反了)🔗 [probability - Graphic model factorizing, marginalization - Cross Validated] https://stats.stackexchange.com/questions/478746/graphic-model-factorizing-marginalization
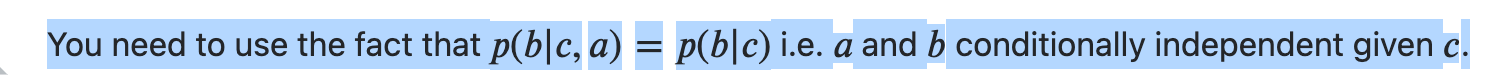
原来如此,现在可以推导出来了:
head-to-head
接下来:

部分证明过程:
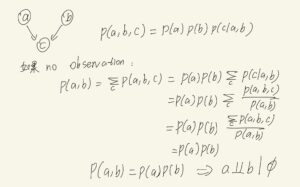
总结
所以对3种基本图模型的总结如下:
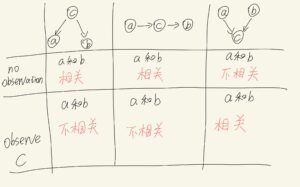
奇怪的记忆法
可以看出,no observation的一横排都比较「符合人类直觉」:可以把「相关」比作「Where's my Water?」游戏的液体混合。
(从左到右)1:由同一个C流出的液体到达了A和B,所以no observation认为A和B可能共享了同一种(来自C的)液体,所以是related;
2:由A流出的液体经过C到达了B,这个肯定可以大胆认为related;
3:A和B都流出了各自的液体,但只是流向了C而已。我们认定A和B不相关看起来也很合理。
于此同时,“observe C”的解释如下:
(从左到右)1:堕落帝国的2个先辈子弟互不相关,无法信息沟通(沟通信息被强大的堕落帝国阻隔);
2:堕落帝国的先辈子弟正在自家星系里观测还没有上天的土著:由于堕落帝国还没觉醒,根本不关心这些小事,所以没有土著的信息,和土著也没关系;
3:由于bug,一个帝国的思潮变成了墙头草,这个帝国能够同时附庸于2个帝国:2个帝国之间仍然保留正常的信息交流,也互相知道了“你和我拥有一个相同的附庸”。
In summary, a tail-to-tail node or a head-to-tail node leaves a path unblocked unless it is observed in which case it blocks the path. By contrast, a head-to-head node blocks a path if it is unobserved, but once the node, and/or at least one of its descendants, is observed the path becomes unblocked.
PRML P376
一道例题
进度有点长,写个临时草稿:
接下来开始做P377的一道题:

做这道题花的时间是在太长,跨越了多个时间点且走了很多弯路,所以最开始的思路已经不连续了。在做题的过程中查找了这些资料:
🔗 [probability - Why is P(A,B|C)/P(B|C) = P(A|B,C)? - Cross Validated] https://stats.stackexchange.com/questions/258379/why-is-pa-bc-pbc-pab-c
🔗 [conditional probability - About calculation of marginalizing (Bishop's book) - Cross Validated] https://stats.stackexchange.com/questions/366550/about-calculation-of-marginalizing-bishops-book
同时再次贴出这个容易搞错的条件概率积分:
特别注意
在PRML的8.30和8.31会遇到类似这样的积分公式:
[mathjax-d]P(G)=\sum_{B} \sum_{F} P(G \mid B, F) \cdot P(B) \cdot P(F) [/mathjax-d]以及
[mathjax-d]P(G \mid F)=\sum_{B} P(G \mid B, F) \cdot P(B)[/mathjax-d]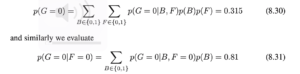
要注意这个公式是有前提条件的:head-to-head模型
最后贴出(重写、重做的)推导过程:
D-separation
preview 学习P378的D-separation
原则:

现在讨论书上的2个bayesian net example:
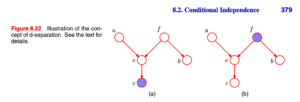
这篇笔记有点长了,是时候开始结尾了。从D-separation的判别开始,接下来会跳跃性地阅读一些章节:
补充:整体马尔可夫性
在清理老旧笔记的时候整合进来的知识
🔗 [bnet_slides.pdf] http://staff.ustc.edu.cn/~jianmin/lecture/AI2014/bnet_slides.pdf

Naive bayes的图模型
naive bayes的图模型

(没完全理解的内容)
(没完全理解)
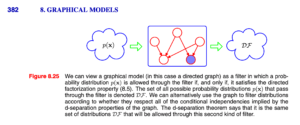
马尔可夫毯
前置内容
在阅读P382的时候补充一个过去的公式(公式8.5):factorization property
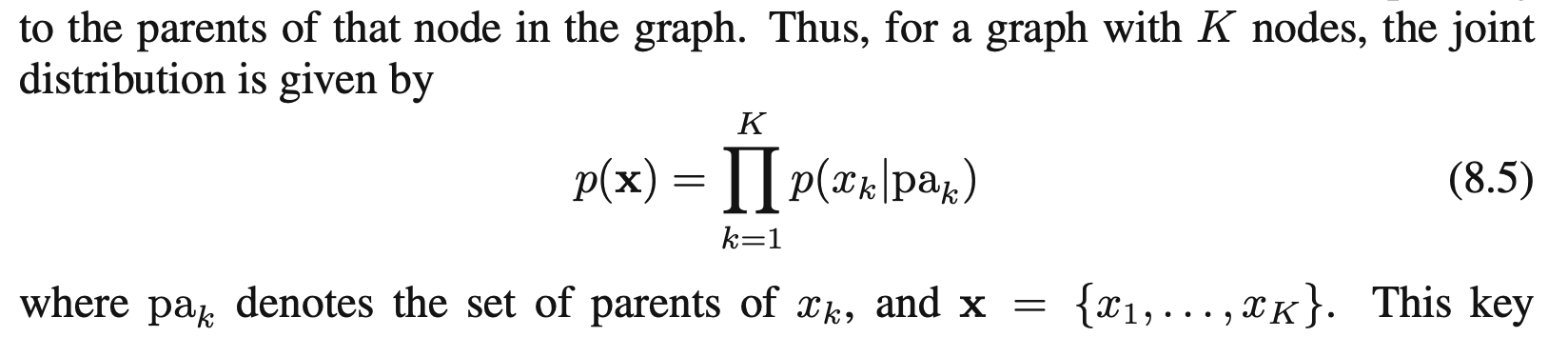
这个公式在上面写的3个基本的图模型模型中已经用到过了,比如:
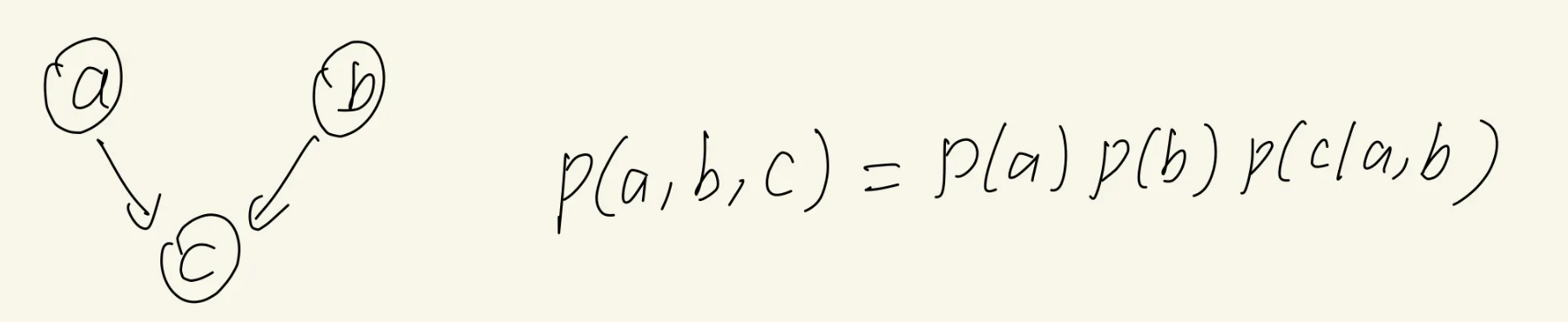
接下来阅读P382~P383
P382,观察这个公式:
[mathjax-d]\begin{aligned} p\left(\mathbf{x}_{i} \mid \mathbf{x}_{\{j \neq i\}}\right) &=\frac{p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{D}\right)}{\int p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{D}\right) \mathrm{d} \mathbf{x}_{i}} \\ &=\frac{\prod_{k} p\left(\mathbf{x}_{k} \mid \mathrm{pa}_{k}\right)}{\int \prod_{k} p\left(\mathbf{x}_{k} \mid \mathrm{pa}_{k}\right) \mathrm{d} \mathbf{x}_{i}} \end{aligned}[/mathjax-d]笔记:
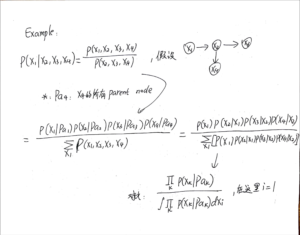
马尔可夫毯-定义和例题
马尔可夫毯/马尔可夫菌毯

解释:
We can think of the Markov blanket of a node [mathjax]x_i[/mathjax] as being the minimal set of nodes that isolates [mathjax]x_i[/mathjax] from the rest of the graph.
P383
现在我们有一个节点[mathjax]x_i[/mathjax],它处在一个巨大的bayesian net当中;
我们以节点[mathjax]x_i[/mathjax]为核心,(通过某些方法)从巨大的有向图当中挖出了一部分节点,构成markov blanket(如上图所示);
如果不做任何优化(不构建这个bayesian net),使用全概率公式计算与[mathjax]x_i[/mathjax]有关的条件概率,则需要拿出所有节点都参与计算,非常复杂且计算量很大;
但是事实上通过构建这个bayesian net并进行消元,我们化简后的条件概率计算公式只需要使用「markov blanket中的节点」就可以了!以这张图为例,markov blanket只有7个节点。
笔记:
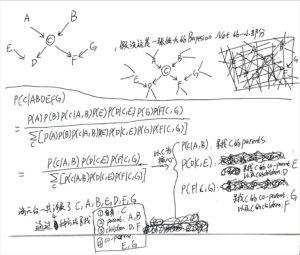
Variable elimination
再学一个就结束本篇笔记:variable elimination
* 限于篇幅(这篇笔记时间跨度太长了,这样不好),本篇笔记的variable elimination只讨论一些简单的内容
在过去的笔记中其实就已经试图学过了,只是当时完全没理解,只会硬套公式:🔗 [2021-11-20 - Truxton's blog] https://truxton2blog.com/2021-11-20/
之前参考的slide写的不明不白(preview),这次决定换一个好的slide来阅读:
发现了这个:
🔗 [scribe_note_lecture4.pdf] https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture4.pdf
不幸的是,variable elimination比我想象的要多很多很多,涉及各个内容,所以本篇笔记暂时不学太深入了,就学一点皮毛知识:
有向图的variable elimination


假设这里有一个bayesian network,A B C D E都是离散的,且各自都有n种可能的情况。
用全概率公式计算P(E)则需要[mathjax]n^5[/mathjax]的计算复杂度:
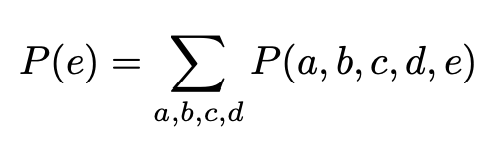
但是,如果使用variable elimination,则只需要[mathjax]4n^2[/mathjax]的复杂度。
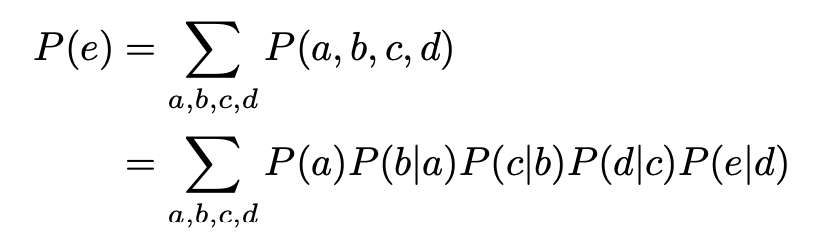
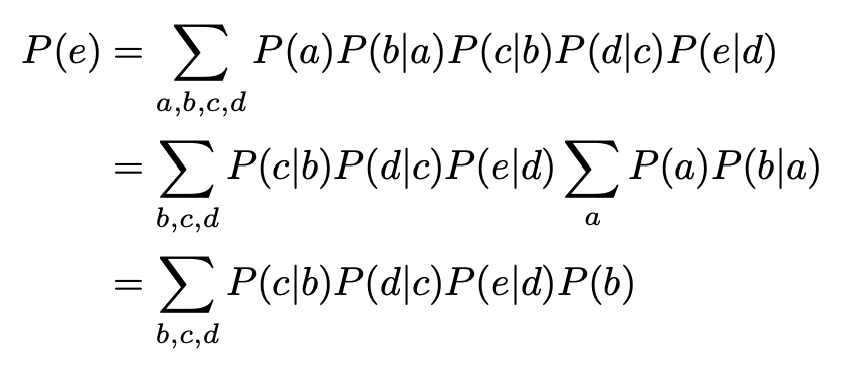
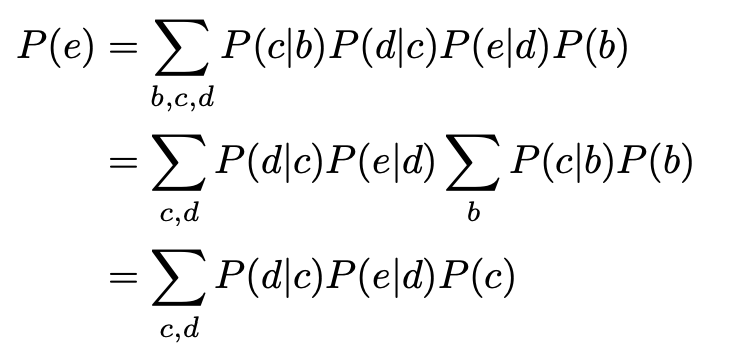
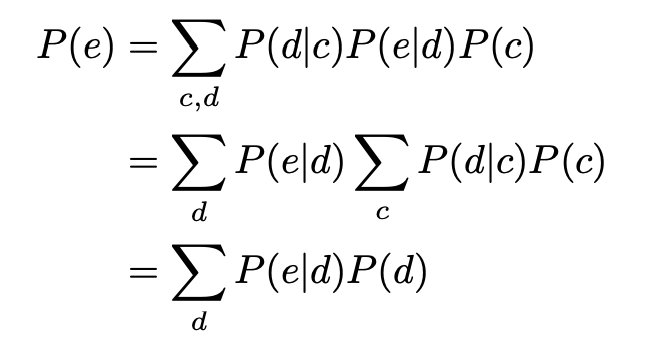
这是一个用存储空间换取时间的优化算法,通过保存“之前的结果”,避免每次都要把整个bayesian net上的所有节点都算一遍。
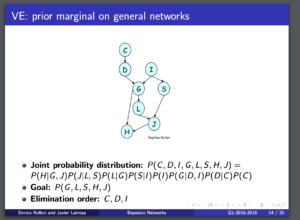
有关这个例题写法的讨论
上面这个例题来自🔗 [Bayesian Networks - Exact Inference by Variable Elimination] https://www.cs.upc.edu/~larrosa/MEI-CSI-files/BN/2-BN-VE.pdf
在学习variable elimination的过程中,我一度认为这个slide里面的写法是错误的,但后来接触到了🔗 [scribe_note_lecture4.pdf] https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture4.pdf 才知道原来我认知有点问题。
example: (在上面这个链接的Page 4)
[mathjax-d]\sum_{y_{1}} P\left(y_{1}\right) P\left(x_{1} \mid y_{1}\right) P\left(y_{2} \mid y_{1}\right)=\alpha_{1}\left(x_{1}, y_{2}\right)[/mathjax-d] [mathjax-d]\sum_{y_{2}} \alpha_{1}\left(x_{1}, y_{2}\right) P\left(x_{2} \mid y_{2}\right) P\left(y_{3} \mid y_{2}\right)=\alpha_{2}\left(x_{1}, x_{2}, y_{3}\right)[/mathjax-d]总结一下variable elimination的推导要点:要大胆,胆大妄为!

所以现在这道例题可以拿出来用了:
HMM variable elimination(Forward-Backward算法的推导原型)
* 下面的推导内容(cs.cmu.edu的slide,以及我按照这个slide的推导)多多少少有点不合群,推导出来的forward-backward和其他参考资料都不一样。虽然结果应该问题不大,但还是推荐看本笔记后面的推导。
HMM variable elimination
继续看这个slide:🔗 [scribe_note_lecture4.pdf] https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture4.pdf
阅读这部分内容:

回顾本篇笔记上面的内容(条件概率求积分的那一部分),这个公式也可以写成:
[mathjax-d]P\left(y_{i} \mid x_{1}, \ldots, x_{T}\right) \propto \sum_{y_{1}} \sum_{y_{2}} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_{T}} P\left(x_{1}, x_{2} \cdots x_{T}, y_{1}, y_{2} \cdots y_{T}\right)[/mathjax-d]上面这部分的推导过程:

这种嵌套累加符号是非常可怕的,计算量会非常非常大!
接下来开始推导HMM variable elimination,这个slide包含的内容非常有用:HMM variable elimination就是forward-backward算法的本质!
备份一下slide的关键页面:
下面开始推导:
另一种推导Forward-Backward的方法
理论上来说这个推导和上面的推导是可以相互转换的,但我暂时没时间验证。
部分推导细节参考了徐亦达老师:https://www.bilibili.com/video/BV1BW411P7gV?p=5