This post was published in 2022-07-26. Obviously, expired content is less useful to users if it has already pasted its expiration date.
从这里开始:🔗 [2022-07-22 - Truxton's blog] https://truxton2blog.com/2022-07-22/#N-gram模型与k-order_Markov_model
尽量使用简单的例子来描述(而不是使用大量公式),方便复习。
Table of Contents
Markov chain/Markov process
Markov chain/Markov process
简单的说就是一个定义好的模型,在这个模型里“未来的状态只和现在的状态有关,与更早的状态无关”。
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.
https://en.wikipedia.org/wiki/Markov_chain
例1:
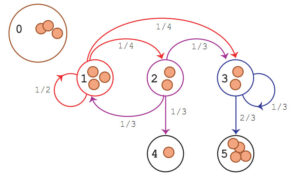
上面这张图是markov chain. 虽然看起来像是“state 3的状态不仅由state 2决定,还由state 1决定”,但实际上这么理解是错误的。正确的理解方法是“从state 1到达state 1/2/3,每个概率(1/2, 1/4, 1/4)都仅仅与当前状态有关”(当然,上面这张图的概率都是常数概率,转移概率当然都只和当前有关。下面举个例子是个反例,“转移概率和之前的状态有关“。
例2:
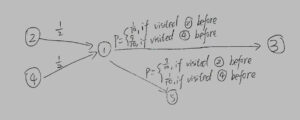
上面这张图不是markov chain. 从state 1到state 3/state 5的概率取决于“在到达state 1之前经过的是state 2还是state 4“.
隐马尔可夫模型(HMM)
隐马尔可夫模型(HMM):
一个对外隐藏了状态的马尔可夫链,我们只能观测到它的(隐藏)状态发射出的数值(称为观测值)。
接下来是3个基本问题:

马尔可夫决策过程(MDP)
马尔可夫决策过程 / Markov Decision Process:
马尔可夫决策过程是马尔可夫链的推广;

更具体的内容见: 🔗 [2021-12-26 - Truxton's blog] https://truxton2blog.com/2021-12-26/#马尔可夫决策_Markov_Decision_Process_基本概念
便于快速复习的西瓜浇水例子:

不完全可观测马尔可夫决策过程
Partially Observable Markov Decision Process,不完全可观测马尔可夫决策过程
这是POMDP第一次出现在本博客,所以这部分可能会写得多一些。
回顾一下MDP过程中的一部分:“根据当前的状态进行决策,系统就会根据决策的内容(用概率决定)跳到下一个状态,同时给予奖励反馈...”,总之,“当前的状态”是 100%明确 。
如果当前的状态无法观测到,就像HMM一样,我们只能得到观测的数值,那么很自然地我们无法像MDP那样“直接根据当前的状态选择下一步的决策”,我们需要通过一些方法去合理猜测当前的状态,然后再进行决策。
所以POMDP可以看作MDP的进一步限制版模型:限制对当前状态的直接获取。
那么如何在POMDP模型里推测当前的实际状态呢?
Because the agent does not directly observe the environment's state, the agent must make decisions under uncertainty of the true environment state. However, by interacting with the environment and receiving observations, the agent may update its belief in the true state by updating the probability distribution of the current state.
https://en.wikipedia.org/wiki/Partially_observable_Markov_decision_process
完整定义如下:

暂停一下,分个类
暂停一下,分个类
所以到目前为止学习的马尔可夫家族已经覆盖这张表了:

Mixed Observable Markov Decision Processes
Mixed Observable Markov Decision Processes, MOMDP
对比一下:Partially Observable Markov Decision Process, POMDP
它们2个到底有什么区别呢?
简单地概括:POMDP有一个缺点就是“状态太多导致置信空间维度爆炸(因为会使用one-hot这一类编码方法)”。而MOMDP就是“按住一部分维度(部分状态我们认为是fully observable)”,把一个高维向量拆分2部分:一个是数值固定的fully observable,另一个是数值不固定的partially observable,这样就能大幅度降低维度了。
注:下面的笔记很乱,且仅仅讨论了MOMDP的最基础用法,不涉及优化算法。
第一次学习的笔记, 完全就是错误的内容,不要乱打开!
总结:
POMDP:所有状态都是不可直接获得的,需要我们去”猜“。
MOMDP:把一个状态因式分解成2种状态:(可直接观测,不可直接观测)。
POMDP的缺点是计算复杂度太高,高达[mathjax]\mathcal O(n^2)[/mathjax]. (推导过程见折叠的部分)
MOMDP本质上是对POMDP进行模型简化,从[mathjax]\mathcal O(n^2)[/mathjax]降到[mathjax]\mathcal O(n)[/mathjax] .
资料1:
MOMDPs are decision-making formalism for high-level planning under mixed full and partial observations.
https://github.com/urosolia/MOMDP
发现了一篇神奇论文:🔗 [A Mixed Observability Markov Decision Process Model for Musical Pitch] https://arxiv.org/pdf/1206.0855.pdf
先看这张图:一个Partially Observable Markov Decision Process模型:
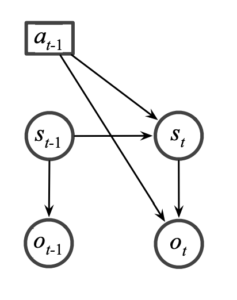
这个很容易理解:当前采取的行动(a)取决于对状态的观察以及对状态的置信程度。
现在我们把单个state拆开:
temp:
现在阅读这里

这个介绍比上面的详细一些


置信空间:四方体模型
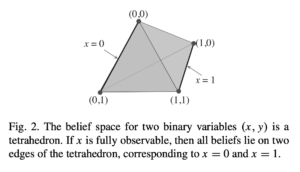
该如何理解呢?首先注意到4个角是由排列组合构成的:(0,0), (0,1), (1,0), (1,1),可以理解为“4个最极端的置信情况”;
现在取x为[0, 1]区间的float,y为[0, 1]区间的float,那么(x,y)就一定会落在这个四方体的内部(包括表平面和4个顶点)。
如果(x, y)落在这个四方体的最中心位置,就表明“此时处在全体置信区间的正中心”;
遇到了一些理解多维置信空间的麻烦,现在参考:🔗 [(6条消息) 马尔可夫模型(MC, HMM, POMDP, MOMDP)_Vic_Hao的博客-CSDN博客_pomdp] https://blog.csdn.net/weixin_42018112/article/details/87908428
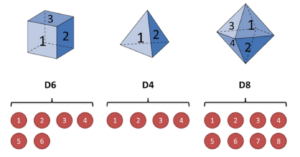
上面这张图容易理解,这些立方体都只使用表面,就像一个骰子。
接下来回到这个正四面体:
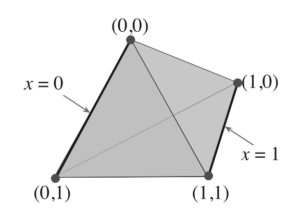
首先是它的体积:[mathjax]\frac{\sqrt{2}}{12} a^{3}[/mathjax](来源)
跑题了,不需要计算那么复杂也能看懂这张图了:

这张图的意思其实很简单:在这个正四面体置信空间里,如果x是“fully observable”,那么它一定是0或者1,所以(x, y)就一定会落在图中2条加粗的边上。
换句话来说,fully observable:一定是0或者1;partially observable:[0, 1]区间上。
最后一句话我们可以猜测:POMDP大概率是使用了整个多面体,而MOMDP只使用了多面体的2条边。
接下来阅读这段文字:

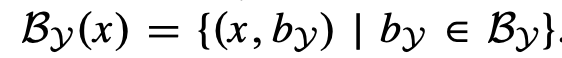
解释:x是fully observable,现在只需要穷举y(partially observable)的所有可能的情况,与x组成tuple (x, y)就可以了!
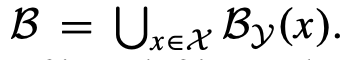
解释:x是fully observable,把所有x的可能都列举出来分别计算tuple (x, y),最后把这些情况都合并起来即可形成一个大空间[mathjax]\mathcal{B}[/mathjax].
所以现在已经很明确了,再总结一遍:在上面的这个正四面体置信空间里,POMDP使用了整个多面体,而MOMDP只使用了多面体的2条边,所以MOMDP的计算量要远小于POMDP!
但是这篇论文(Planning under Uncertainty for Robotic Tasks with Mixed Observability)并没有提到四面体之外的置信空间,只是提到了“POMDP的计算量是指数增长”:

发现了这个:
🔗 [jpineau-dagstuhl13.ppt] https://www.cs.mcgill.ca/~jpineau/talks/jpineau-dagstuhl13.pdf
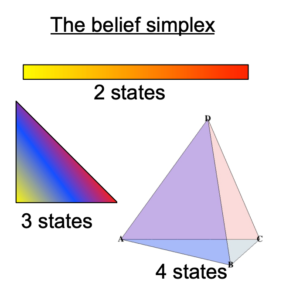
好像找到规律了:
2种状态:1维空间:1条边(2*1/2)
3种状态:2维空间:3条边(3*2/2)
4种状态:3维空间:6条边(4*3/2)
5种状态:4维空间:10条边(5*4/2)
6种状态:5维空间:15条边(6*5/2)
....
n种状态:(n-1)维空间:[mathjax]\frac{n*(n-1)}{2}[/mathjax] 条边
....
等等,为什么5种状态需要四维空间?因为三维空间里不存在“正五面体”:🔗 [五面体 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-hans/五面體
等等,这个四面体的顶点描述和《Planning under Uncertainty for Robotic Tasks with Mixed Observability》论文中的顶点描述不太一样!一个是A,B,C,D,一个是(0, 0), (0, 1) ...
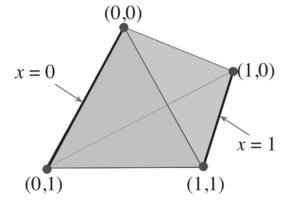
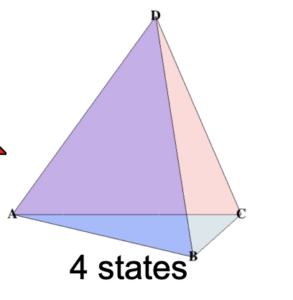
我的想法就是说...如果顶点的tuple不是(0, 0)的枚举,而是(0, 0, 0)的枚举,那我们是不是需要构造一个“27顶点多面体”呢?又或者:
这玩意应该怎么用类似(0, 0)的模组描述?
事实上是:上面的想法出现了问题!
事实上,上面的2个正四方体根本不是一个东西!一个是“由state数量决定了顶点数量的多维空间中的多面体,正四面体只是其中的一种情况”,另一个是“MOMDP的简化算法模型” .
为什么会有(0, 0)呢?因为这是(x, y)!那x和y到底是什么呢?是”概率”,一个constant value!
那高维度的置信模型应该怎么描述才对呢?
(x, y),x是“对多维向量求相似度”,y也是“对多维向量求相似度”!即使是一个10000000000维的模型(10000000000种state),也会得到(x, y):(constant, constant).
所以说这个正四面体到底是什么?是:“无论我们处在什么维度上,我们都会用到这个正四面体,它和维度无关”!
所以说还会出现类似(x, y, z)这样的情况吗?目前学到的MOMDP模型里并没有涉及到额外的观测值,所以我们只需要考虑(x, y)即可!
所以说计算复杂度应该如何计算?
注:n是state的数量。
首先观察这张图,我们可以这样思考:
从空间中取任意一点,我们应该拿它和「所有顶点」都分别求一次距离(最后取距离最近的顶点作为最大置信猜测值),由于空间是(n-1)维空间,所以我们每次计算距离的时候都需要复杂度O(n),最后得到的复杂度应该是[mathjax]\mathcal O(n^2)[/mathjax],这就是POMDP的复杂度。
而MOMDP的复杂度应该是O(n):从空间中取任意一点,我们应该拿它和「某2个指定的顶点」分别求一次距离,由于空间是(n-1)维的,所以复杂度只和维度有关;又因为维度和state数量线性相关(维度=state-1),所以复杂度为O(n).
再补充一些想法:
首先我们把POMDP的state因式分解成(x, y)是要增加复杂度的!直接从[mathjax]\mathcal O(n^2)[/mathjax]变成了[mathjax]\mathcal O(n^3)[/mathjax]!但我们在MOMDP模型进行了降维打击,直接从3维空间打击成了1维空间,降了2个维度,所以最终变成了[mathjax]\mathcal O(n)[/mathjax].
这个思路明显有大问题,停!重新看论文并重新写笔记。
对《Planning under Uncertainty for Robotic Tasks with Mixed Observability》论文的第二版笔记草稿
笔记草稿
重新开始写
首先讨论这句话:

等等,为什么维度突然爆炸成这个样子了?我的思路还停留在发射常数的HMM模型上。
原来如此,上面这张图的各种参数是“必须取枚举类型数值”的,比如说10x10的格子,机器人一定会落在某一个格子,而不会落在一个(float, float)的坐标系上。
而MFCC(39维,39个float)和chromagram(12维,12个flat)是和这个不一样的。
以chromagram举例:
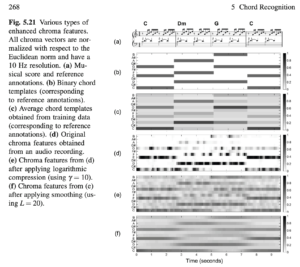
12维的向量,12个float的大小是有意义的,是连续的,数值大的数字代表「更偏向,权重更大,更接近」。比如一个chromagram向量写为[10.1, 0, 0, 0, 0, ... 0],很明显就是告诉我们“该chroma向量非常非常接近chroma C”.
而论文中的机器人状态明显是离散的值。

再举一个例子:
假设分类数据集[玫瑰花,兰花,水仙花,桃花],不使用one-hot的情况下是[1, 2, 3, 4],现在有对一朵花的识别数据8组:1, 1, 2, 4, 4, 4, 4, 4,最后 错误地使用连续数据学习算法(比如求平均值)判定出结果 是3-水仙花。这明显是不合理的。这个时候就需要用one-hot进行处理了!
所以最后回到论文中的机器人状态建模,就很容易理解为什么是12500维了:全部都是离散的分类型状态。
所以接下来的一段也很好理解了:把12500维中的部分维度“固定住”(fully observable),把剩下的partially observable的维度抽出来单独排放,这样就可以大幅度降维了。

现在再看这张图片:

我认为我应该是被这张图给误导了。这张图根本没有那么重要,它只是一个x=0或1、y=0或1的简单例子。

这张图才是重要的:将一个高维置信空间变为若干个低维置信空间的集合(并集)。
换句话来说论文里所谓的“因式分解”(factored model)本质上就是把一个k维的向量变为 m维 和 (k-m)维 2个向量。
再讨论这个复杂度:

现在暂时认为复杂度大概是[mathjax]\mathcal O(S^3)[/mathjax]. 首先:需要计算某个空间向量和其他所有向量“顶点”的相似度(注意这里是one-hot编码的离散特征分类,需要逐个比较一次),其次计算2个S维向量之间的距离/相似度时还需要O(S)的时间复杂度。
相对应地,MOMDP只是把复杂度从原来的[mathjax]\mathcal O(S^3)[/mathjax]降为[mathjax]\mathcal O(k^3)[/mathjax],k取决于“能找到多少fully observable特征”。
未完成的内容:

从这里开始暂时离开这篇论文,回到之前的那篇很短的小论文识别note上面。
🔗 [A Mixed Observability Markov Decision Process Model for Musical Pitch] https://arxiv.org/pdf/1206.0855.pdf
太短了,反正我不知道论文在说什么东西:

还是回到《Planning under Uncertainty for Robotic Tasks with Mixed Observability》继续看吧:
完美的理论模型已经学过了,然而这个模型不能直接拿来用,因为现实场景存在一些限制:

没有任何一种特征是从头到尾都fully observable的,这个时间点是fully observable,下一个时间点没准就不是了。
优化方法
暂时略过
先看到这里为止吧:
查阅这部分内容相关资料的时候涉及到了一些超出范围的拓扑学内容,部分笔记和有用链接见:🔗 [2022-07-27 - Truxton's blog] https://truxton2blog.com/2022-07-27/
k-order Markov model
k-order markov model
就是NLP领域常用的N-Gram,它是马尔可夫链的变种。标准的马尔可夫链是2-gram(bigram),“某一时刻t的状态只和前一刻t-1的状态有关”;n=3时就是3-gram(trigram),“某一时刻t的状态和(前一刻t-1、前一刻的前一刻t-2)有关”;n=4时就是“某一时刻t的状态和(前一刻t-1、前一刻的前一刻t-2、前一刻的前一刻的前一刻t-3)有关” ...
🔗 [2022-07-22 - Truxton's blog] https://truxton2blog.com/2022-07-22/#N-gram模型与k-order_Markov_model
Variable-order Markov model
variable-order markov model
好像还和k-order markov model的定义略有不同。

Markov blanket
马尔可夫毯
* 以下内容直接从🔗 [贝叶斯网络 - Truxton's blog] https://truxton2blog.com/bayesian-network-introduce/#马尔可夫毯-定义和例题 原封不动复制过来,可能存在更新不及时的问题(以原笔记的内容为最新版)
前置内容
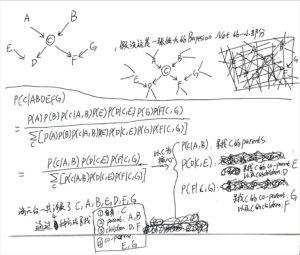
在阅读P382的时候补充一个过去的公式(公式8.5):factorization property
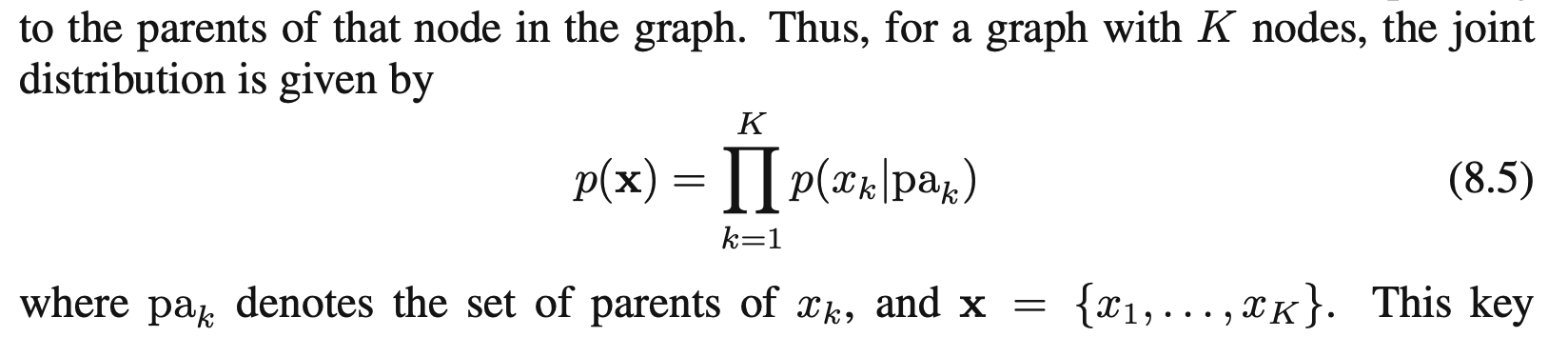
这个公式在上面写的3个基本的图模型模型中已经用到过了,比如:
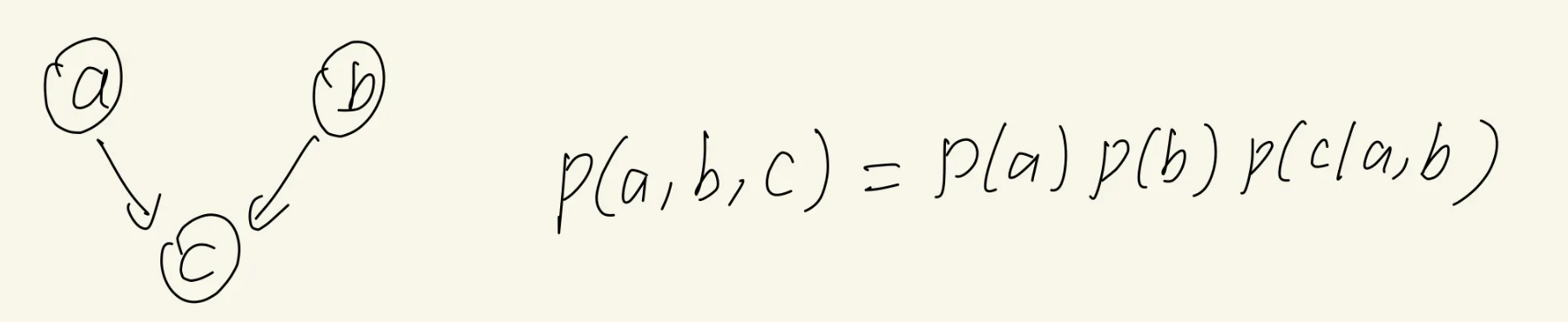
接下来阅读P382~P383
P382,观察这个公式:
[mathjax-d]\begin{aligned} p\left(\mathbf{x}_{i} \mid \mathbf{x}_{\{j \neq i\}}\right) &=\frac{p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{D}\right)}{\int p\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{D}\right) \mathrm{d} \mathbf{x}_{i}} \\ &=\frac{\prod_{k} p\left(\mathbf{x}_{k} \mid \mathrm{pa}_{k}\right)}{\int \prod_{k} p\left(\mathbf{x}_{k} \mid \mathrm{pa}_{k}\right) \mathrm{d} \mathbf{x}_{i}} \end{aligned}[/mathjax-d]笔记:
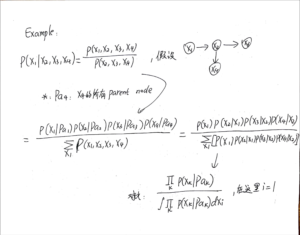
马尔可夫毯-定义和例题
马尔可夫毯/马尔可夫菌毯

解释:
We can think of the Markov blanket of a node [mathjax]x_i[/mathjax] as being the minimal set of nodes that isolates [mathjax]x_i[/mathjax] from the rest of the graph.
P383
现在我们有一个节点[mathjax]x_i[/mathjax],它处在一个巨大的bayesian net当中;
我们以节点[mathjax]x_i[/mathjax]为核心,(通过某些方法)从巨大的有向图当中挖出了一部分节点,构成markov blanket(如上图所示);
如果不做任何优化(不构建这个bayesian net),使用全概率公式计算与[mathjax]x_i[/mathjax]有关的条件概率,则需要拿出所有节点都参与计算,非常复杂且计算量很大;
但是事实上通过构建这个bayesian net并进行消元,我们化简后的条件概率计算公式只需要使用「markov blanket中的节点」就可以了!以这张图为例,markov blanket只有7个节点。
笔记: