WARNING: This article may be obsoleteThis post was published in 2022-08-25. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今天从哪里开始？
下面是一些杂乱的前置引导内容：
接着学习三角函数和傅里叶：🔗 [2022-06-09 - Truxton's blog] https://truxton2blog.com/2022-06-09/
搞定了2022-06-09笔记中的 三角函数的正交性 （离散版本的证明更难一些，2022-09-10才补完），现在继续：
复数、欧拉公式、极坐标
先把欧拉公式写在最前面
由于这部分内容是2024年补充上去的，所以某些书写习惯（比如虚数的j写在前面）可能和本篇笔记的推导内容不太一样。
[mathjax-d]e^{j\theta}=\cos(\theta)+j\sin(\theta)[/mathjax-d]
[mathjax-d]e^{-j\theta}=\cos(\theta)-j\sin(\theta)[/mathjax-d]
复数与极坐标
参考资料
复习极坐标，非常有用，具体见本文后面的笔记：（网页备份截图）🔗 [复数的几种表示形式 | Mengqi's blog] https://mengqi92.github.io/2015/10/06/complex/
🔗 [复数的几种表示形式 | Mengqi's blog] https://mengqi92.github.io/2015/10/06/complex/
🔗 [极坐标系 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/极坐标系
🔗 [复数 (数学) - 维基百科，自由的百科全书] https://zh.wikipedia.org/zh-hans/复数_(数学)#极坐标形式
复数与极坐标的最基础知识
复数：[mathjax]4+3i[/mathjax]
直角坐标：[mathjax](r\cos(\theta), r\sin(\theta))=(4, 3)[/mathjax]
复数极坐标：[mathjax](r, \theta) = (5, \arctan(\frac{3}{4}))[/mathjax]
复数的一些基本运算：
欧拉公式
引导资料
欧拉公式
欧拉有一天发现，神奇数字[mathjax]e[/mathjax]的纯虚数次方竟然在复数平面上绕圈！
https://mengqi92.github.io/2015/10/06/complex/
证明欧拉公式有点头大，在失去知觉之前先把浏览器里打开过的Tab都记录下来：
（最有用的，虽然最后没有并没有完全参考这个思路）🔗 [Intuitive Understanding Of Euler’s Formula – BetterExplained] https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/
（可以看作上面那个链接的中文转译版）🔗 ["上帝公式"(欧拉公式)真的神到无法触碰？ - 知乎] https://zhuanlan.zhihu.com/p/48392958
当然还有一些用泰勒公式直接展开证明的：
🔗 [用 e^x 的泰勒展开证明欧拉公式是否正确？ - 知乎] https://www.zhihu.com/question/26135850
🔗 [泰勒公式到欧拉公式的推导_进击的路飞桑的博客-CSDN博客泰勒公式证明欧拉公式] https://blog.csdn.net/jgj123321/article/details/96438301
欧拉公式的推导（不使用泰勒展开）
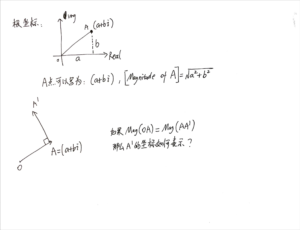
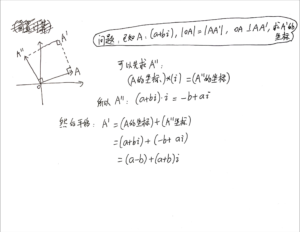
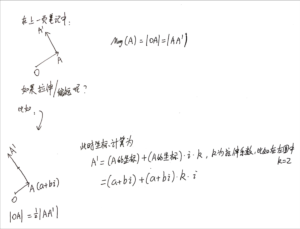
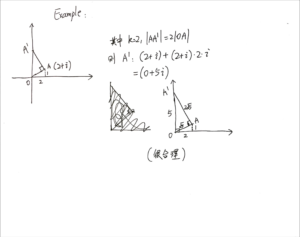
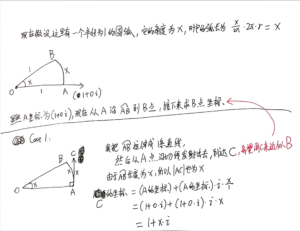
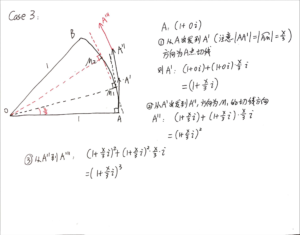
* 注意：下面这张图Case n的符号写错了，x应该是n，公式应该是
[mathjax-d]\lim_{{\color{red}{n}}\to +\infty}(1+\frac{1}{n})^n=e[/mathjax-d]
（虽然这个错误应该很容易发现）
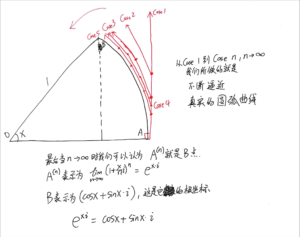
复数波与实数波
有了欧拉公式后，现在我们可以回到信号处理方面的内容了：复数波和实数波
注意：[mathjax]e^{ix}[/mathjax]这玩意还会被称为 Exponential Signal . （来源），exponential signal分解为real signal或imaginary signal，它们（real和imaginary）都被称为sinusoidal signal.
[mathjax-d]A e^{i(\omega t+\phi)}=A e^{i(2 \pi f t+\phi)}=A \cos (2 \pi f t+\phi)+i A \sin (2 \pi f t+\phi)[/mathjax-d]
也可以用这张图来理解：
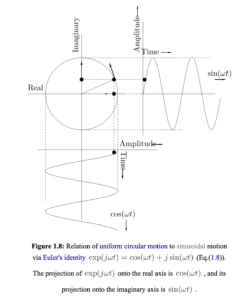
同时注意欧拉公式的一个变体公式：
[mathjax-d]\begin{aligned} &\cos (\theta)=\frac{e^{i \theta}+e^{-i \theta}}{2} \\ &\sin (\theta)=\frac{e^{i \theta}-e^{-i \theta}}{2 i} \end{aligned}[/mathjax-d]部分杂乱的~jos博客笔记
接下来切换到~jos的博客：
🔗 [Complex Sinusoids] https://ccrma.stanford.edu/~jos/fp/Complex_Sinusoids.html
注意到复数波的写法略有区别：用[mathjax]j[/mathjax]表示虚部
[mathjax-d]A e^{j(\omega t+\phi)}=A e^{j(2 \pi f t+\phi)}=A \cos (2 \pi f t+\phi)+i A \sin (2 \pi f t+\phi)[/mathjax-d]接下来是complex amplitude/phasor：link1, link2
[mathjax-d]\text{complex amplitude/phasor} \triangleq \mathcal{A} \triangleq A e^{j \phi}[/mathjax-d]之所以这样称呼，是因为：
[mathjax-d]Ae^{j(\omega t+\phi)}=Ae^{j\phi}\cdot Ae^{j\omega t}[/mathjax-d]这样就可以把[mathjax]Ae^{j\phi}[/mathjax]看作一个整体，这样就可以把它看作Amplitude.
阅读这里：🔗 [Complex Sinusoids as Circular Motion] https://ccrma.stanford.edu/~jos/fp/Plotting_Complex_Sinusoids_Circular.html
首先复习这个公式：
[mathjax-d]e^{i\theta}+e^{-i\theta}=2\cos(\theta)[/mathjax-d]它可以这样理解：要想产生一个不含虚部的实数波[mathjax]\cos(\theta)[/mathjax]，必须用这个原则来组合复数波：
For the signal to be real, every positive-frequency complex sinusoid must be summed with a negative-frequency sinusoid of equal amplitude.
https://ccrma.stanford.edu/~jos/fp/Plotting_Complex_Sinusoids_Circular.html
哎呀，前面学的内容有点偏了（学到滤波器那边去了），（~jos的网页需要花点时间适应他的排版， 滤波器 和 DFT for audio 是两个不同的合集）
重新回到“学习fourier”的正轨上！
从这里重新开始：（这是总目录）🔗 [MATHEMATICS OF THE DISCRETE FOURIER TRANSFORM (DFT) WITH AUDIO APPLICATIONS SECOND EDITION] https://ccrma.stanford.edu/~jos/mdft/mdft.html
（遇到了404的~jos/stanford.edu网页，学习终止！）
接下来学什么？
算了，重新来这里吧：🔗 [[台湾大学] 李琳山 信号与系统_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1dM4y1M7LK
（写在2022-08-27的笔记中）
补充一些复数小知识
补充1
还有哪些东西没涉及到？
复数的绝对值/复数的模：
本笔记前面学习了复数的magnitude（强度），当然实际上它也可以这样表示：
[mathjax-d]|a+b i|=\sqrt{a^{2}+b^{2}}[/mathjax-d]然后我们能得到一个非常重要的东西：
[mathjax-d]\left| e^{j\omega_0 t} \right|=\cos^2(\omega_0 t)+\sin^2(\omega_0 t)=1[/mathjax-d]应用举例：
补充2
还有哪些东西没学到？
极坐标的另一种表示方法
在学习了复数的模以后，极坐标[mathjax]C[/mathjax]就可以这样表示：
[mathjax-d]C=\left| C \right| e^{j\theta}[/mathjax-d]当然这是显而易见的：
来源：奥本海姆信号与系统P15
补充3
还有哪些东西没学到？
如果n为自然数，那么[mathjax]e^{j2\pi n}[/mathjax]永远为1.
这个结论很有用，在推导离散周期信号的时候会用到：（奥本海姆信号与系统P19）
[mathjax-d]\mathrm{e}^{\mathrm{j}\left(\omega_{0}+2 \pi\right) n}=\mathrm{e}^{\mathrm{j} 2 \pi n} \mathrm{e}^{\mathrm{j} \omega_{0} \pi}=\mathrm{e}^{\mathrm{j} \omega_{0} \pi}[/mathjax-d]接着我们分析一下[mathjax]e^{j\pi n}[/mathjax] .
不知道脑子是不是出了问题，居然忘了这个：[mathjax](a^n)^m=a^{nm}[/mathjax]（wikipedia）
所以：
[mathjax-d]e^{j\pi n}=(e^{j\pi})^n=\left[\cos(\pi)+j\sin(\pi)\right]^n=(-1)^n[/mathjax-d]可以用来直观解释为什么离散信号在[mathjax]\omega_0=\pi[/mathjax]的时候“振荡最激烈”。（奥本海姆信号与系统P20）
补充4
[mathjax-d]\frac{1}{j}=-j[/mathjax-d]这个补充知识看起来很弱智，但这确实是我没注意到的内容。有些时候推导公式的时候往往计算到[mathjax]\frac{1}{j}[/mathjax]就停下来了，实际上还能再算一步的。
