This post was published in 2023-06-19. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
多项式时间
属于多项式时间:[mathjax]O(1)[/mathjax], [mathjax]O(\log{(n)})[/mathjax], [mathjax]O(n)[/mathjax], [mathjax]O(n^2)[/mathjax], ... [mathjax]O(n^{1000})[/mathjax], ...
不属于多项式时间:[mathjax]O(n!)[/mathjax], [mathjax]O(2^n)[/mathjax], [mathjax]O(n^n)[/mathjax], ...
P问题
复杂度
每个学校的算法课的前几节的必学内容。
参考资料:🔗 [P (複雜度) - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/P_(複雜度)
在度理論中,P(polynomial time class)是在複雜度類別問題中可於確定型圖靈機以多項式量級(或稱多項式時間)求解的決定性問題。
P通常表示那類可以「有效率地解決」或「溫馴」的可計算型問題,就算指數級非常高也可以算作「溫馴」,例如RP與BPP問題。當然P類別存在很多現實處理上一點也不溫馴的問題,例如一些至少需要[mathjax]n^{10000000}[/mathjax]指令來解決的問題。很多情況下存在著更難的複雜度問題。
https://zh.wikipedia.org/wiki/P_(複雜度)
比如brute-force配对的复杂度是[mathjax]O(n^2)[/mathjax],merge-sort复杂度是[mathjax]O(n\log{(n)})[/mathjax]
可以参考以前的笔记:🔗 [2021-10-19 - Truxton's blog] https://truxton2blog.com/2021-10-19/#各大主流排序算法的时间复杂度
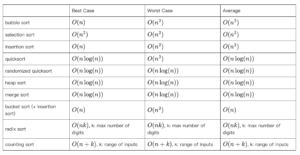
暴力匹配算法的复杂度
问题:
暴力图片相似度匹配算法,或者暴力的地理位置相似度匹配算法,复杂度是多少?是否属于P问题?
* 暴力图片相似度匹配:我有[mathjax]N[/mathjax]张图片,但我只会一种简单的算法:比较2张图片的相似度。我不会做任何聚类等处理。所以我要把第[mathjax]1[/mathjax]张图片和第[mathjax]2\sim N[/mathjax]张图片进行相似度对比,把第[mathjax]2[/mathjax]张图片和第[mathjax]3\sim N[/mathjax]张图片进行对比...直到搞定第[mathjax]N-1[/mathjax]和第[mathjax]N[/mathjax]张图片的相似度对比。
* 暴力的地理位置相似度匹配算法同理。
复杂度是[mathjax]O(n^2)[/mathjax](而不是[mathjax]O(n^n)[/mathjax])
因为是n+n+n+n+...+n (n个n)= [mathjax]n*n[/mathjax] = [mathjax]n^2[/mathjax]
n代表什么
看到这句话(来自🔗 [P (複雜度) - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/P_(複雜度))

先来猜想一下最弱智的质数判断:暴力尝试,比如判断一个特大数n,可以从[mathjax]2[/mathjax]一直试到[mathjax]n-1[/mathjax].
等等,即使是最弱智的方法,复杂度 似乎 也仅仅是[mathjax]O(n)[/mathjax]而已,如果使用稍微优化一点的方法也应该是[mathjax]O(\sqrt{n})[/mathjax],这当然是P问题,但为什么直到2002年以后才被解为P问题?
先看看🔗 [Is finding prime numbers in P or NP? - Quora] https://www.quora.com/Is-finding-prime-numbers-in-P-or-NP
🔗 [Is the AKS primality test faster than just testing all prime divisors up to a numbers square root? : r/askmath] https://www.reddit.com/r/askmath/comments/5hj9tb/is_the_aks_primality_test_faster_than_just/
🔗 [Why isn't the naive prime test (iterate from 1 to sqrt(n) to test n) considered polynomial O(sqrt(n))? Why was the AKS primality test a breakthrough if there are trivial ways to test in T(n) <= O(n)? - Quora] https://www.quora.com/Why-isnt-the-naive-prime-test-iterate-from-1-to-sqrt-n-to-test-n-considered-polynomial-O-sqrt-n-Why-was-the-AKS-primality-test-a-breakthrough-if-there-are-trivial-ways-to-test-in-T-n-O-n
下面这个链接似乎匹配了我的问题:
🔗 [computational complexity - Why isn't the naive PRIMES algorithm in P? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/294079/why-isnt-the-naive-primes-algorithm-in-p
所以好象是明白了。大家讨论的[mathjax]n[/mathjax]都是 整数的长度 [mathjax]n[/mathjax],而不是 整数的大小 [mathjax]n[/mathjax]!
比如我随便在下面敲一堆数字:
1928346501982736408912736401823764012这个数字对应的[mathjax]n[/mathjax]只有37而已!
如果要用数字的位数表示[mathjax]n[/mathjax]并用最传统的方法(从2试验到n-1),我们确实就需要指数倍的时间复杂度[mathjax]10^n[/mathjax]。这当然远远超出了我们普通图灵计算机的范畴,所以这个算法不属于P.
这就是为什么直到2002年才出现质数检验证明为P问题的论文。问题确实是一个复杂又难的问题,不是那些传统弱智手段能相比的。
NP问题
再看看NP
🔗 [NP (複雜度) - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/NP_(複雜度)
P問題是指在多项式时间内可以找出解的決定性問題(decision problem),而NP問題則包含可在多项式时间內驗證 其解 是否正確,但不保證能在多項式時間內能找出解的決定性問題。
https://zh.wikipedia.org/wiki/NP_(複雜度)
需要特别注意上面的红字。(本笔记的后面还有一个例子)
一个很容易懂的例子:地图上色问题。来自:🔗 [价值百万美元的问题 -- P vs NP 问题 (音频讲稿) - 知乎] https://zhuanlan.zhihu.com/p/68652786

决定性问题
为了避免奇奇怪怪的举例...
学了一个下午,发现写这篇笔记的时候最容易出现的问题就是 乱举例 ,结果最后发现“连举出的例子都不符合定义”。
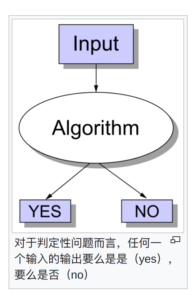
🔗 [決定性問題 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/決定性問題
所以说这种问题不是决定性问题:“给定某个图G...找出一个最优方案,使得...”,但这种问题往往可以通过某些方案转换成决定性问题。
决定性问题的解
决定性问题的解一定要是一个正确的解吗?什么是正确?
见本笔记稍后的co-NP.
P与NP的关系
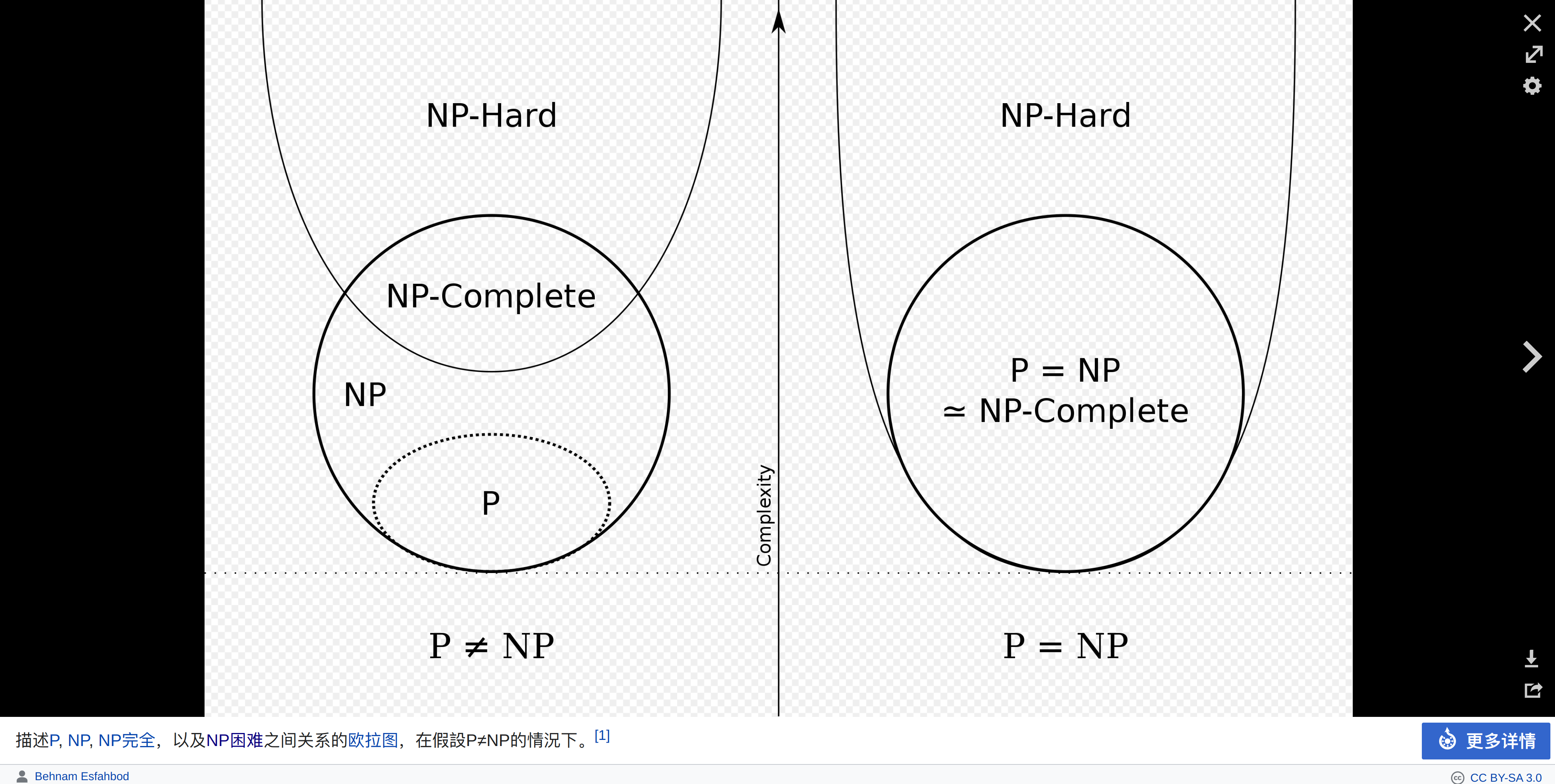
之所以下面这张图有左右2种假设,是因为P是否等于NP仍然是未解决的问题。
🔗 [P np np-complete np-hard - NP (複雜度) - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/NP_(複雜度)#/media/File:P_np_np-complete_np-hard.svg
但这张图需要注意的是:NP-Hard指的是上面那个抛物线的所有内容,所以说NP-complete也是np-hard的一部分!
还要注意,NP指的是下面那个圆的全部,所以说np-complete和p都是np的一部分!
解释:
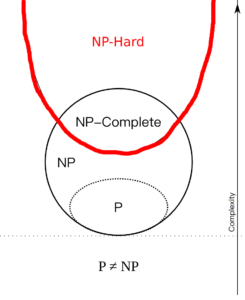
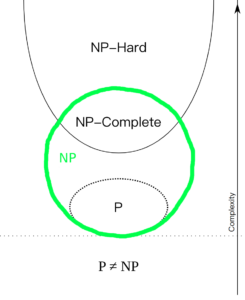
原图如下:
co-NP问题
超出NP范畴的问题:co-NP
原始问题:我一直在思考,NP问题给出的“解”,必须是正确的解吗?这个“正确”到底是什么?有些“解”可以解决整个问题,有些“解”只是娱乐性质拿来验证用的。
一开始我想破了头也没想清楚(所以这篇笔记的草稿写了又删删了又写),但后来我学到了coNP,一下子就懂了。
以哈密顿回路为例(🔗 [哈密頓路徑 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/哈密頓路徑):
问题1:给定某个图,这张图里存在哈密顿回路吗?
问题2:给定某个图,这张图里不存在哈密顿回路,对吗?
而我给出的“解”也有2种:一种是哈密顿回路,它可以被快速验证,并且“有用”;另一种是我随手画的“路径”,当然不是哈密尔顿回路,它也可以被快速验证(被快速验证为是错误的),但卵用没有。
这2个问题可能在“是”与“否”的层面上有点耍赖,想要回答“存在哈密顿回路”,只需要给出任意一个正确答案;想要回答“不存在哈密顿回路”,就必须给出所有情况并得出结论,或者用严格的方法进行证明。
另一个讨论:🔗 [complexity theory - Not Hamiltonian is in NP Class? - Computer Science Stack Exchange] https://cs.stackexchange.com/questions/39539/not-hamiltonian-is-in-np-class
所以coNP的概念就出现了:🔗 [co-NP - Wikipedia] https://en.wikipedia.org/wiki/Co-NP
此外,我注意到:
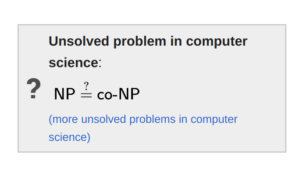
目前一般是认为NP!=co-NP的。
回到之前的哈密顿回路问题,根据这两个链接:ref1, ref2:
| 问题 | 分类 | 更进一步的分类 | 原因 |
| determining whether a graph is Hamiltonian | NP | NP-complete | 只需要展示一个Hamiltonian回路就可以【肯定】问题 |
| determining whether a graph is NOT Hamiltonian | co-NP | co-NP-complete | 只需要展示一个Hamiltonian回路就可以【否定】问题 |
最后再补充一个总结:
NP只需要能够验证“是”的回答就满足定义了。能够验证“否”的回答属于Co-NP问题。
https://www.zhihu.com/question/318575253/answer/639708409
再举一个例子:“验证质数”,这个问题在2002年前才被证明为P问题,但它在2002年以前就是一个NP/co-NP问题吗?
(* 事实上,验证质数的历史不仅仅只有NP/P/co-NP,还有一堆奇奇怪怪的RP/ZPP等更深的概念)
In computational complexity theory, the formal language corresponding to the prime numbers is denoted as PRIMES. It is easy to show that PRIMES is in Co-NP: its complement COMPOSITES is in NP because one can decide compositeness by nondeterministically guessing a factor.
In 1975, Vaughan Pratt showed that there existed a certificate for primality that was checkable in polynomial time, and thus that PRIMES was in NP, and therefore in [mathjax]\mathsf {NP\cap coNP}[/mathjax].
🔗 [Primality test - Wikipedia] https://en.wikipedia.org/wiki/Primality_test
注意到上面的引用里有一个很重要的推断:如果一个问题的“补集问题”(反问题)属于NP,那么这个问题属于co-NP.
所以:1975年前,质数检测:co-NP,只需要展示一个整除的因数(不能为1或者自身)就可以(在polynomial time内)【证否】
1975年前:合数检测:NP,因为只需要展示一个整除的因数(不能为1或者自身)就可以(在polynomial time内)【证明】
1975~2002,质数检测:NP,只需要找到一个特征(certificate)就可以(在polynomial time内)【证明】
1975~2002,合数检测:NP,因为只需要展示一个整除的因数(不能为1或者自身)就可以(在polynomial time内)【证明】
2002年以后,质数检测/合数检测:P,因为AKS解决了质数检测为P的同时也顺便解决了合数检测为P
NP-hard和NP-complete
np-complete并不是可以随便定义/随便举例的问题,而是众多科学家经过研究/推导以后转换/归纳出来的问题。可以理解为“精选问题”。(本笔记后面还有np-complete的解释笔记)
先看这个:🔗 [P问题、NP问题、NP完全问题和NP难问题 - 知乎] https://zhuanlan.zhihu.com/p/73953567
再次回顾这张图:

再看这个:🔗 [怎么理解 P 问题和 NP 问题? - 知乎] https://www.zhihu.com/question/27039635
引用上面链接的某个回答一部分:
NP-hard:如果某个问题S是NP-hard,那么对于任意一个NP问题,我们都可以把这个NP问题在多项式时间之内转化为S,并且原问题的答案和转化后S的答案是相同的。也就是说只要我们解决了S,那么就解决了所有的NP问题。
NP-complete:一个问题既是NP-hard,又在NP里面;也就是说
1. 解决了这个问题我们就解决了所有NP问题
2. 这个问题本身也是个NP问题
https://www.zhihu.com/question/27039635/answer/101730260
另一个类似的资料:来自:🔗 [NP (复杂度) - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-cn/NP_(複雜度)

NP-complete和世纪难题P-NP
np-complete是非常重要的概念,因为它意味着“精选的问题”:
🔗 [NP完全 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh-cn/NP完全

现在被证明是NPC问题的有很多,任何一个找到了多项式算法的话所有的NP问题都可以完美解决了。因此说,正是因为NPC问题的存在,P=NP变得难以置信。
🔗 [什么是P问题、NP问题和NPC问题 | Matrix67: The Aha Moments] http://www.matrix67.com/blog/archives/105
任意一个NPC问题被多项式算法解决为P问题=100万美金=世纪难题的终结,也就是说P=NP成立了。
背包问题,leetcode/竞赛算法题,NPC问题,动态规划
在上面的这张图里我们看到背包问题是一个NPC问题
等等...一道题是NPC问题,但为什么会拿来作为一道经典的动态规划题?NPC问题不是还没法用多项式公式解决的吗?
🔗 [背包问题可以通过动态规划解决,为什么还说背包问题是NPC的? - 知乎] https://www.zhihu.com/question/20686504
下面是一些解释:
好像明白了...是不是和本篇笔记之前想半天的“质数检验”差不多道理,你以为这是 数值大小 的多项式算法,但别人讨论的是 数值位数 的多项式算法。
所以可以看这里:🔗 [什么是伪多项式时间算法? - 知乎] https://www.zhihu.com/question/20013122
在这个回答里面我又看到了关于质数测试的解释:
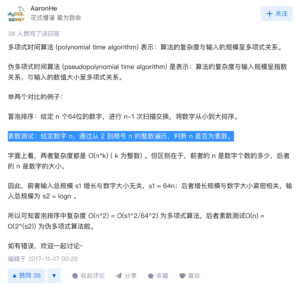
所以问题就解决了。动态规划算法未必就是NP,也有可能是NP-hard,比如01背包问题的动态规划算法就不是NP/NPC,而是np-hard,因为它所用的时间并不是多项式时间,而是伪多项式时间。
背包问题是一个NP-complete的组合优化问题,Search的方法需要[mathjax]O(2^N)[/mathjax]时间才能获得最优解。而使用动态规划,我们可以在伪多项式(pseudo-polynomial time)时间内获得最优解。
🔗 [Knapsack Problem 背包问题 - Huahua's Tech Road] https://zxi.mytechroad.com/blog/sp/knapsack-problem/