This post was published in 2023-07-06. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
2024年的补充
本篇笔记的作业大概是这么做的:
- 有一份参考答案🔗 [Solution manual to „Introduction to Linear Optimization“ by Dimitris Bertsimas | Solverer] https://solverer.com/library/dimitris_bertsimas/introduction_to_linear_optimization
- 我知道参考答案肯定比我自己瞎想的推导更严谨,但我还是在某些证明上试图使用“自己能理解”的思路去推导
- 所以本篇笔记应该是有很多错误的
前情提要:已经学会了什么
前情提要:
大概搞清楚了这门课的前1/3部分大概是要做什么(讨论什么问题,解决什么问题),
(浪费了一些时间学一些前置内容)范函,欧拉法,牛顿法:🔗 [MIT 6.251J Introduction To Mathematical Programming前置知识学习(2023-06-16) - Truxton's blog] https://truxton2blog.com/2024-06-16-learn-mit-intro-to-mathematical-programming/
(浪费了一些时间学一些前置内容)NP, NP-hard相关的话题:🔗 [NP hard相关的话题 - Truxton's blog] https://truxton2blog.com/np-hard-related-topics/
差不多学会了最基本的simplex algorithm:🔗 [(2023年6月)Introduction to Linear Optimization学习笔记1 - Truxton's blog] https://truxton2blog.com/2023-06-intro-to-linear-optimization-learning-notes-1/
作业
目前学会的这点东西肯定是不够做作业,但不知道学完simplex algorithm以后从什么地方开始学起,所以还是从作业开始吧:🔗 [Assignments | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/assignments/

Exercise 1.2
题目
P34 Ex1.2

和convex有关的概念:凸集,凸函数,凸锥(等)
凸集,凸函数(更严谨的一般定义和证明)
之前在simplex algorithm里面顺带学过,但只是知道定义,不知道规范的表达方法,以及这个凸字到底有什么影响
凸集
《最优化理论与算法》P10

最关键的内容:用[mathjax]\lambda x^{(1)}+(1-\lambda)x^{(2)}, \lambda \in [0,1][/mathjax]来表示两个点[mathjax]x^{(1)}[/mathjax]和[mathjax]x^{(2)}[/mathjax]之间的任意一点([mathjax]\lambda[/mathjax]为0或1就表示两个点[mathjax]x^{(1)}, x^{(2)}[/mathjax]本身)
一道入门例题,适合初学者:


注意[mathjax]\lambda \in [0,1][/mathjax]是不等式能继续推导的关键。

注意这道题要用[mathjax]\lambda_1[/mathjax]和[mathjax]\lambda_2[/mathjax],而不是[mathjax]d_1[/mathjax]和[mathjax]d_2[/mathjax].

前2个可以“想象”一下
第3和第4个要稍微难“想象”一些,要依赖公式推导
凸锥

待补充
一些对比图
🔗 [中科大-凸优化 笔记(lec4)-凸集和凸锥_凸锥笔记_及时行樂_的博客-CSDN博客] https://blog.csdn.net/qq_41485273/article/details/113696648
待补充
极点

极点这个概念在之前学习simplex algorithm的时候反复出现(但在之前的笔记里我一般用“顶点”来称呼)
(注意,这里先跳过一堆东西,比如极方向,Gordan定理,等等)
凸函数,严格凸函数
p17
是凸函数,但不是强凸函数的例子:[mathjax]y=x[/mathjax]
附带一个简单例题:

一些凸函数的后续推论

一道简单的例题,虽然比较抽象但使用简单的公式(凸集和凸函数的定义)就可以证明:

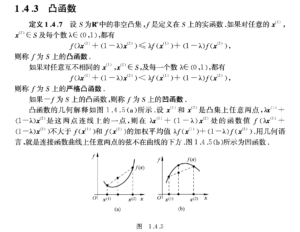
分段线性凸函数
还是不够做Ex 1.2
chatgpt让我去学 分段线性凸函数, piecewise linear convex objective functions
后续补充:这张图能帮助快速理解这个名词是什么:
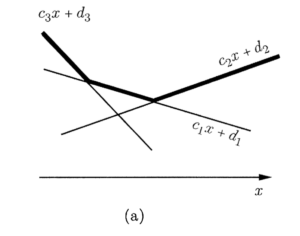
《最优化理论与算法》没有专门讲这个概念
但在《Introduction to Linear Optimization》这本书里提到了:

看MIT p15~p16
貌似和这个有关:
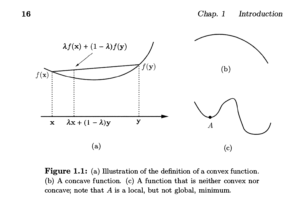
但并没有在一开始就介绍什么是piecewise linear convex objective function,所以还要继续看几页
p15先按正常流程介绍凹凸函数
然后介绍常见的这种样子的函数(局部极小值未必等于全局最小值):
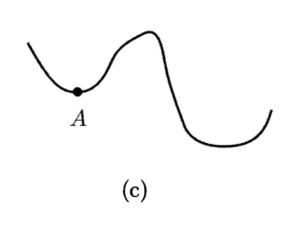
然后开始介绍这个所谓的“分段线性凸函数”:

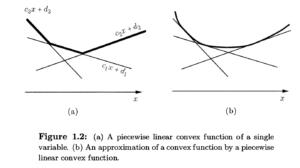
然后P16介绍了分段线性凸函数“为什么凸”的证明方法(以及一个引定理):
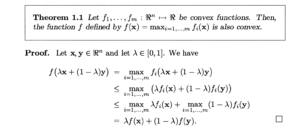
证明过程不难,可以跟着书本正常推导
紧接着介绍了线性分段凸函数的用途:
p16~p17,从蓝色的地方开始读
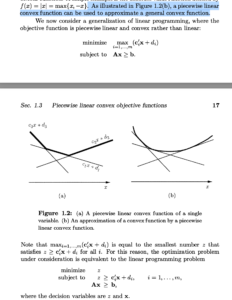
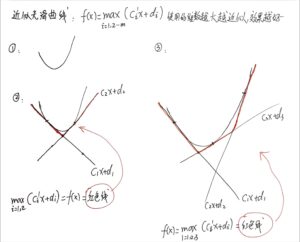
做Exercise 1.2过程中查的零碎知识
下面这些都是在做exercise 1.2的过程中遇到的:
数学符号:
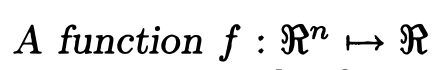
意思是这个函数[mathjax]f[/mathjax]输入的是[mathjax]n[/mathjax]维变量,输出的是一个标量。
affine function
仿射函数
MIT P15
🔗 [仿射函数、线性函数的区别? - 知乎] https://www.zhihu.com/question/52571431

P15有一个以前没见过的凸函数特质:

p15
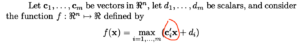
这里的[mathjax]c^{\prime}_{i}[/mathjax]有个prime:[mathjax]\prime[/mathjax],在这里其实是矩阵转置的意思,也就是说[mathjax]c^{\prime}_{i}[/mathjax]相当于[mathjax]c^{T}_{i}[/mathjax]
Exercise 1.2的解答草稿
现在已经可以做Exercise 1.2的第一问了!

目前由于不够熟练,红框的部分还是不能快速反应,要看一会才能发现原来就剩最后一步了。
再看第二问
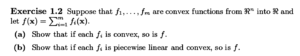
如果理解题意了似乎也不难。关键在于如何在一开始读懂题目并把初始目标理清。
(b)的翻译:多个 分段线性凸函数 的和仍然是一个 分段线性凸函数 ,也就是说,我们可以把(b)分成2部分:
- 多个 分段线性函数 的和仍然是一个 分段线性函数 ;
- 多个 凸函数 的和仍然是一个 凸函数
然后我们发现第2部分(多个 凸函数 的和仍然是一个 凸函数 )已经在(a)证明出来了。所以我们只需要证明第1部分即可。非常简单。就是乘法分配律。

Exercise 1.5
题目
搞定1.2了(应该),再看下一题:exercise 1.5
🔗 [Assignments | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/assignments/


(a)部分:Linear programming formulation

先看a:linear programming formulation
发现没看过这个概念,所以翻回p18~p19:其中p19有一个例题,同时p18解释了p19的例题为什么要这样做:

怎么看都像是“化标准型”的一个前置规范类型(不是那么标准),但实际上思路和逻辑不能按照之前的“化标准型”来理解,因为这里并没有把不等号转化为等号。我之前没有遇到过带有绝对值的化标准型问题,所以理解上面这张图的Example 1.5花了一点时间:
尤其是注意到“while the second yields”的答案,第一眼看上去怪怪的,其实这样写是没问题的,这样写就意味着[mathjax]x_1^+[/mathjax]和[mathjax]x_1^-[/mathjax]至少有一个是0.

(b)部分
再看b:

暂时无法理解为什么有(b)这一问。看起来一切都是显而易见的(如果做了(a)问以后),为什么这玩意还需要证明?
当然,两个去掉绝对值的公式是等价的,可以把它们转化为相同格式的标准型(虽然我觉得这一步根本不需要,但如果不加这一步第(b)问就是零工作量):

(c)部分
再看(c):

二维空间最容易画图,但即使如此,要找一个好例子也不容易,因为有一个[mathjax]y=\left| x \right|[/mathjax]的等式放在这里(而不是一个不等式形成的一大片空间),导致最终的限制区域就是在[mathjax]y=\left| x \right|[/mathjax]上面取线段,或者最终的限制区域就是[mathjax]y=\left| x \right|[/mathjax]本身(这样的话就没法举例了)
所以无论如何,[mathjax]Ax+By\leq b[/mathjax]起码要“穿过”[mathjax]y=\left| x \right|[/mathjax]才行,像这样:
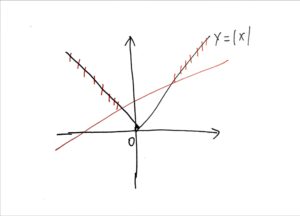
多试几次就能找到一个例子了:
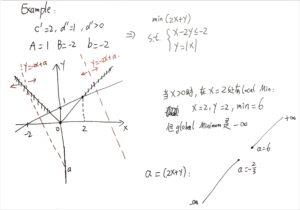
当然这个例子其实也不是很好,因为在这里global minimum是[mathjax]-\infty[/mathjax],不知道[mathjax]-\infty[/mathjax]能不能被算作global minimum.
不管了,先结束这道题吧。现在(a) (b) (c)都做完了。
Exercise 1.11 Optimal currency conversion
题目
再看下一题吧:
Exercise 1.11 Optimal currency conversion

一些思路
最后补充的备注:这道题的大概意思是明白了,但有一个细节非常难办([mathjax]u_i[/mathjax]),反正目前我想不通到底怎么做比较好。网上也没找到什么(能让我看明白)的解答。
错误的思考过程
这道题一度让我想起了markov的一些定理,但由于(时间问题)我只能把我的一些想不通的问题写下来等待后续思考)
(应该是正确的答案)整个货币兑换的步骤可以这样理解:
- 把B个货币1先用某些策略换成各种货币(仅一次)
- 大喊一次“开换!“,然后这些货币都用各自分配的策略向其他货币兑换一次(仅一次)
- 马上检查货币N有多少,越多越好。
或者可以想象我们有一壶水,然后把它倒在一个N孔容器里,喊一句“开喷!”,马上这些水就(不可逆转的)喷出来了,容器的底部用N个槽来接水。每个孔洞都有自己的喷水分配比例(可能喷给N个容器的任何一个),而且这些水喷完以后就可以开始统计了(不需要把水拉回来重新喷一遍)。
这道题的关键在于, 我们只关心结果,不关心过程 。也就是说,到底通过什么奇妙的方法(或者最少的步数)转换出最终结果的,我们完全不关心,我们只关心一点:每一次转换是否合法,以及每一次转换之后得到的结果是否“更好”一些。
所以说,这道题我们构造出的矩阵不能往“时间轴”的方向去想,比如说类似“横轴/纵轴代表交易的轮次“这样的想法。
这道题的思路首先是构造一个矩阵,它代表的含义是“每一次交易之前制定的计划”。而我们的任务是:找到某个最强大的矩阵满足我们的目标,但其实我们并不关心这个矩阵到底是怎么从初始状态转移过来的,至少在这道题里是这样。
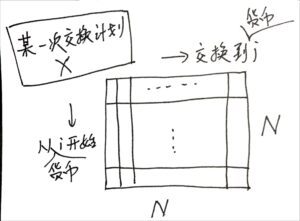
然后我们开始理解某些行/某些列的意义,以及一些顺手写出来的约束/目标条件:
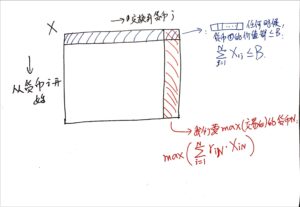
然后我们思考一些约束条件/策略:
假如某个时刻,我们确实拥有了一些货币#N(目标),但我们还要继续交易。那么我们有必要去“动”那些已经换过来的货币#N吗?
无论如何都不需要。我们只需要按住这部分已经得到的货币#N即可,然后操作其他货币。因为根据某些约束条件,这些货币#N一旦离开货币#N,换回来的时候就一定少了一些。
同理,在(非初始状态)的某个时刻,我们可能拥有一些货币#1吗?这个很难说,并不是没有可能。但我们可能把一些不是货币#1的货币交易成货币#1吗?当然不可以,因为这样做一定会亏钱。我们所有的货币都是货币#1提供的初始资金,一旦离开货币#1就绝对不能换回去。注意这里的条件是“一旦离开”。
所以我们要给这个矩阵加一点点限制:
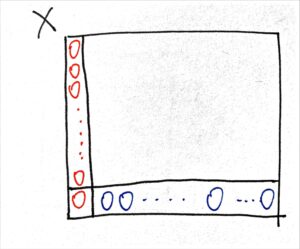
注意这个矩阵的最左上角[mathjax]x_{0,0}[/mathjax]和最右下角的[mathjax]x_{N,N}[/mathjax]也设定成了0,怎么说呢...似乎不是0也可以,但设定为0绝对不会违背题目的限制(有谁会自己换自己的货币?)
最后我们发现还有一个极其恶心的条件没有用上:[mathjax]u_i[/mathjax]. 这个[mathjax]u_i[/mathjax]限制的似乎是“整个流程”(on any given day),而整个流程似乎是“在某一天里进行多轮交易,次数不限“,我只能在最终公式里强行加上一个[mathjax]\sum_{t}[/mathjax]来强行代表一下多轮交易的时间叠加。
硬写答案
如果现在还是要硬写答案,这道题就变成了:
\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}
Use matrix $X$ to indicate the state/plan before each transaction: row=from currency $i$, column=to currency $j$.
\par
our goal is to maximum currency \#N in a certain state:
\[ \max(\sum_{i=1}^N r_{iN} \cdot X_{iN}) \]
\par
And in any time/state, the currency \#1's value should not be larger then initial value B:
\[ \sum_{j=1}^{N}X_{1,j} \leq B \]
\par
And each currency's daily transaction limit:
\[\sum_t\sum_{j=1}^N X_{i,j}\leq u_i, \forall i\]
And some other constraints: we can't transfer any non-\#1 currency to \#1 currency, and we can't transfer any \#N currency out (to other currencies):
\[ X_{i1}=0, \forall i \]
\[ X_{Nj}=0, \forall j \]
\par
so, the linear optimizing equation is:
\begin{alignat*}{3}
& \text{minimize} & \sum_{i=1}^N r_{iN} \cdot X_{iN} & \\
& \text{subject to} \quad& \sum_{j=1}^{N}X_{1,j} \leq B\\
&& \sum_t\sum_{j=1}^N X_{i,j}\leq u_i, \forall i \\
&& X_{i1}=0, \forall i \\
&& X_{Nj}=0, \forall j
\end{alignat*}
\end{document}
最后的latex公式没对齐,好丑,而且这道题也没完全搞明白...但不管了,先放在这里。网上看到的一些解法,包括
🔗 [Exercise 1.11 (Optimal currency conversion) from solution manual to Introduction to Linear Optimization by Dimitris Bertsimas | solverer.com – online solution manuals] https://math.solverer.com/library/dimitris_bertsimas/introduction_to_linear_optimization/exercise_1-11
🔗 [ido_solution07.pdf] https://sma.epfl.ch/~niemeier/opt09/ido_solution07.pdf
都在最后的公式总结里躲开了[mathjax]u_i[/mathjax]这个恶心的限制条件。
编程题:简单的AMPL解线性规划
然后是编程题:
🔗 [Assignments | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/assignments/

似乎不需要看那么长的题,直接翻到第9页:

开始翻译成编程语言...稍等,先学点AMPL lang.
找到一个教程直接开学:
🔗 [ampl_tutorial.pdf] https://www.cs.uic.edu/~hjin/files/ampl_tutorial.pdf
(第2~3页)

然后就写出来了:
果然prismJS没有AMPL language
随便开个文本文件(但在这里为了以后的什么.mod和.dat规范,还是写成一个.mod文本文件)
option solver minos;
var x1 ;
var x2 ;
var x3 ;
var x4 ;
var x5 ;
maximize cost :60*x1+40*x2+30*x3+30*x4+15*x5 ;
subject to con1 : x1+x2+x3+x4+x5<=7;
subject to con2 : 4*x1+2*x2+2*x3+2*x4+x5<=8;
subject to con3 : x2+x4<=3;
subject to con4 : x1<=1.8;
subject to con5 : x3<=0.3;
subject to con6 : x1+x2+x3<=3.8;
subject to con7: x4+x5<=3.2;
subject to con8: x2>=0.5;
subject to con9: x4>=0.5;
subject to con10: x5>=0.4;
subject to con11: x1>=0;
subject to con12: x2>=0;
subject to con13: x3>=0;
subject to con14: x4>=0;
subject to con15: x5>=0;
solve ;运行命令:
ampl: include '/PATH/TO/run.mod';然后得到结果:
MINOS 5.51: optimal solution found.
2 iterations, objective 145然后在命令行里追问一些细节并得到对应的回复:
ampl: display cost;
cost = 145
ampl: display _varname , _var ;
: _varname _var :=
1 x1 0.4
2 x2 2.5
3 x3 0
4 x4 0.5
5 x5 0.4
;至于什么.mod和.dat分离的事情就以后再说吧
搞完了。
编程题:python版本
过了几天杀回来追加点东西
反正写AMPL lang写的我难受,google简单搜索了以后我直接上python-pulp
反正Assignment 2的编程题没有限制语言(话说回来,为什么这门课只有2个编程题?)
初始代码参考了🔗 [Python Pulp库求解线性规划问题(一) 初试线性规划 - 知乎] https://zhuanlan.zhihu.com/p/91285682
把上面这道编程题改成python-pulp版本
*注明:下面的程序在2023-11-25经历了一次重要修改,具体内容见本篇后面的笔记
from pulp import *
prob = LpProblem("demo", LpMaximize)
x1 = LpVariable("x1")
x2 = LpVariable("x2")
x3 = LpVariable("x3")
x4 = LpVariable("x4")
x5 = LpVariable("x5")
prob += 60 * x1 + 40 * x2 + 30 * x3 + 30 * x4 + 15 * x5
prob += x1 + x2 + x3 + x4 + x5 <= 7
prob += 4 * x1 + 2 * x2 + 2 * x3 + 2 * x4 + x5 <= 8
prob += x2 + x4 <= 3
prob += x1 <= 1.8
prob += x3 <= 0.3
prob += x1 + x2 + x3 <= 3.8
prob += x4 + x5 <= 3.2
prob += x2 >= 0.5
prob += x4 >= 0.5
prob += x5 >= 0.4
prob += x1 >= 0
prob += x2 >= 0
prob += x3 >= 0
prob += x4 >= 0
prob += x5 >= 0
prob.solve()
print("Status:", LpStatus[prob.status])
if prob.status == 1:
for v in prob.variables():
print(v.name, "=", v.varValue)
print('maximum result: ' + str(value(prob.objective)))
运行结果:
Welcome to the CBC MILP Solver
Version: 2.10.3
Build Date: Dec 15 2019
command line - /root/miniconda3/envs/py311/lib/python3.11/site-packages/pulp/solverdir/cbc/linux/64/cbc /tmp/244e834729d6476290460646925d2413-pulp.mps max timeMode elapsed branch printingOptions all solution /tmp/244e834729d6476290460646925d2413-pulp.sol (default strategy 1)
At line 2 NAME MODEL
At line 3 ROWS
At line 20 COLUMNS
At line 53 RHS
At line 69 BOUNDS
At line 75 ENDATA
Problem MODEL has 15 rows, 5 columns and 27 elements
Coin0008I MODEL read with 0 errors
Option for timeMode changed from cpu to elapsed
Presolve 5 (-10) rows, 5 (0) columns and 17 (-10) elements
0 Obj 41 Dual inf 175 (5)
6 Obj 145
Optimal - objective value 145
After Postsolve, objective 145, infeasibilities - dual 0 (0), primal 0 (0)
Optimal objective 145 - 6 iterations time 0.002, Presolve 0.00
Option for printingOptions changed from normal to all
Total time (CPU seconds): 0.00 (Wallclock seconds): 0.00
Status: Optimal
x1 = 0.0
x2 = 2.5
x3 = 0.0
x4 = 0.5
x5 = 2.0
maximum result: 145.0和AMPL结果一致。以后就用它了!
2023-11-25补充:使用pulp需要注意的Infeasible打印问题
从2023年7月开始长达4个月,我都一直使用同一个pulp代码模版求解简单的LP问题(主要是为了验证结果),但突然我发现原本使用的代码有重大问题:求解结果不是optimal的时候也会打印出变量数值。
看这个结果:
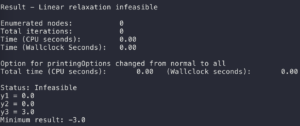
明明是Infeasible,却打印出了后续的结果,很多时候往往看走眼了,根本没注意到Infeasible,对着一个错误的答案猛看猛想。再回想起来,过去的4个月还真的有怀疑过pulp的代码是不是有问题,其实根本原因是我没注意到输出结果里有个Infeasible.
所以一定要加判断: