This post was published in 2023-06-16. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
写在2024年的笔记回顾
写这篇笔记的时候甚至还不知道linear programming (LP)是什么,所以当时也无法辨认出这个"introduciton to Mathematical Programming"到底是什么方向的公开课。所以这篇笔记里面包含了很多(对于线性规划而言)非必需的知识。总之这篇笔记就是一个学习过程,下面的内容在学习顺序上会非常混乱。
从2024年的角度来看,这个公开课的内容以及配套的书(Introduction to Linear Optimization)都属于更“数学”的LP(相比于另一本LP and network flows而言)。书本里面包含了一部分从LP过渡到一般凸优化问题的章节(比如一些重要凸优化引理的推导),而LP的Tableau相关内容被弱化了。
本笔记在2024年8月才整理发表出来,大部分原始内容都不会进行删减(除非发现重大错误)。
大纲
🔗 [Syllabus | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/syllabus/
大纲:
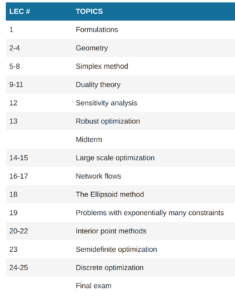
看着像是线性优化/凸优化入门/图论/...的内容。
优化问题
🔗 [Formulations] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/72668234e7184363ade764713fac5bfc_MIT6_251JF09_lec01.pdf
pdf P3

第一条,就是函数导数为0寻找极值点,微积分入门就学过:
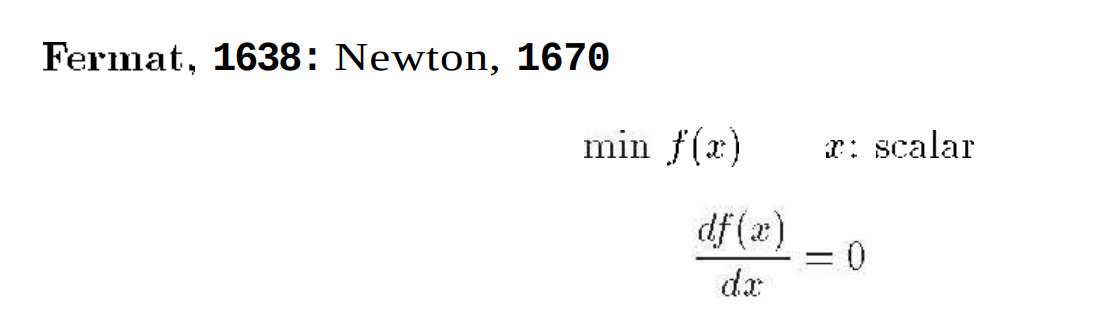
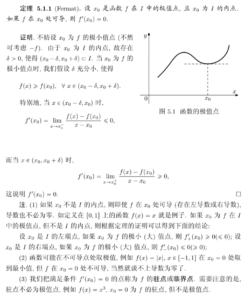
非常简单的example:
给定[mathjax]f(x)=x^2[/mathjax],求它的“最低点/极小值”
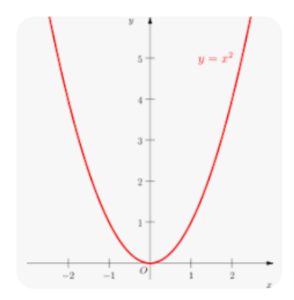
当然是x=0时[mathjax]f(x)=0[/mathjax].
用计算机硬跑,那就是划定个大概的范围,然后f(x=-100), f(x=-99.9999), f(x=-99.9998)...这样跑下去。
欧拉-拉格朗日方程
第2条,欧拉-拉格朗日方程
Euler-Lagrange,🔗 [歐拉-拉格朗日方程 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/歐拉-拉格朗日方程
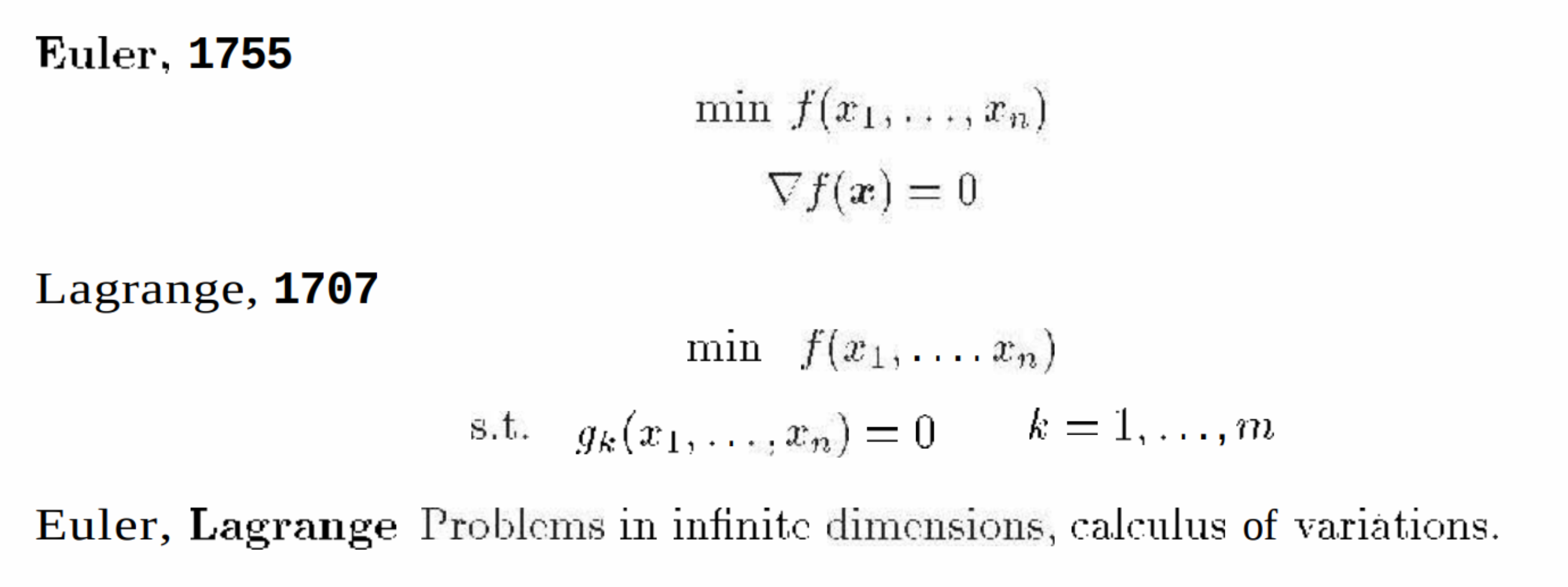
简单的exmaple:
给定[mathjax]f(x,y)[/mathjax]为bivariant gaussian,大概这个样子:
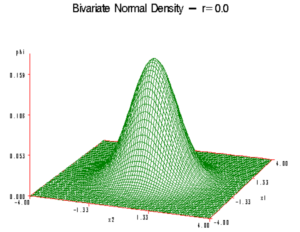
现在要寻找它的极大值(x和y分别为多少的时候[mathjax]f(x,y)[/mathjax]有极大值,就是图中那个“山包”的顶点)
用计算机硬算仍然勉强可行,但计算量已经非常大了,但接下来还要面临指数爆炸的问题
或者另一个例子:

然后再拓展到[mathjax]f(x,y,z)[/mathjax]以及更多的[mathjax]f(x_1, x_2, x_3, x_4...x_n)[/mathjax]
这就是Euler-Lagrange要解决的问题
(跑去临时学了把Euler's method以及复习了一下牛顿法,无关主题,但也写在本笔记里面了)
关键词:泛函,变分
完全看不懂的资料如下:
🔗 [寻找“最好”(2)——欧拉-拉格朗日方程 - 我是8位的 - 博客园] https://www.cnblogs.com/bigmonkey/p/9519387.html
🔗 [泛函、变分和欧拉-拉格朗日方程 | BurningBright] https://www.linchenguang.com/2019/06/07/functional-variation-and-Euler-Lagrange-equation/
🔗 [该怎么理解泛函以及变分?是一种什么思想,老师讲的听不懂。? - 知乎] https://www.zhihu.com/question/26527625
🔗 [LagrangeMultipliers.pdf] https://people.duke.edu/~hpgavin/cee201/LagrangeMultipliers.pdf
把lecture 1的PDF又整体看了一遍,发现(至少从目前来看)真的不需要学会推导Euler-Largrange.
所以就随便一点:

以二维高斯举例,想象一下“极小值点”是一个“很平”的点。
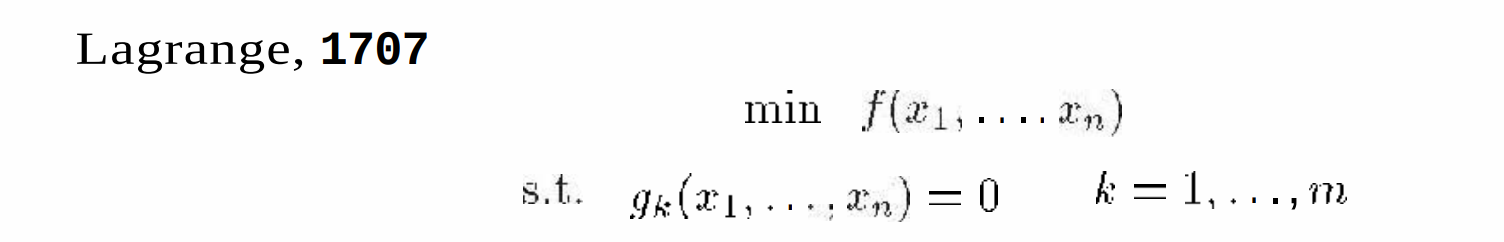
等等,这个[mathjax]g_k[/mathjax]是什么意思?
🔗 [约束优化法_百度百科] https://baike.baidu.com/item/约束优化法/9081297
这里先跳到一个单独的目录:NP hard
欧拉折线法和牛顿法
可能存在歧义的另一个Euler's method
因为一开始查错资料了,只看到Euler,就查成了Euler's method
也顺便学一下基本用途吧:
欧拉方法/欧拉折线法,Euler's method
在此之前要补充一点东西:
补充内容:函数,微分方程,常微分方程,偏微分方程...等一系列概念,只需要理解概念就可以!
🔗 [微分方程 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/微分方程
举例:
已知[mathjax]y^{\prime}=\sin(x)[/mathjax],求函数[mathjax]y[/mathjax](用[mathjax]y=f(x)[/mathjax]表达)
当然是[mathjax]y=-\cos(x)+C[/mathjax].
现在有了一个更难的问题:
已知[mathjax]y^{\prime}=y,\ y(0)=1[/mathjax],求函数[mathjax]y[/mathjax](用[mathjax]y=f(x)[/mathjax]表达)
实际上是[mathjax]y=e^x[/mathjax],但如果我们没学过正规的方法,想出这种答案就只能靠猜(看看学过的常见函数里有没有对得上的)
如果猜不动呢?就只能上Euler's method了
这个例题就在下面的视频里作为引题出现了:
(这个视频并不难,不需要纸笔推导,非常容易就理解了,如果忘记了Euler's method完全可以快速看一遍作为复习)🔗 [Euler's method | Differential equations| AP Calculus BC | Khan Academy - YouTube] https://www.youtube.com/watch?v=q87L9R9v274
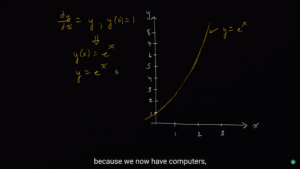
假设我们并不想得到什么解析解
然后视频开始阐述如何用 折线 来近似这条曲线:
先从[mathjax]x=0, y=1[/mathjax]出发,用某个固定的斜率往右上方走:
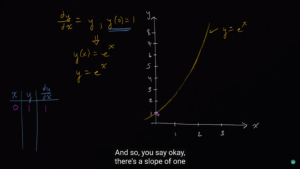
应该如何往右上方走呢?使用[mathjax]y^{\prime}(1)=y=1[/mathjax], 假定/模拟 接下来从[mathjax]x=0[/mathjax]走到[mathjax]x=1[/mathjax],使用了常数斜率[mathjax]1[/mathjax]. 所以我们会走到[mathjax]x=1,\ y=2[/mathjax]这个位置。
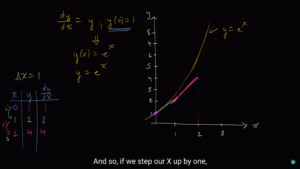
然后在[mathjax]x=1,\ y=2[/mathjax]的位置继续走,使用[mathjax]y^{\prime}(2)=y=2[/mathjax]作为斜率,走到[mathjax]x=2,\ y=4[/mathjax]这个位置
然后继续走...每走一次,x都增加1
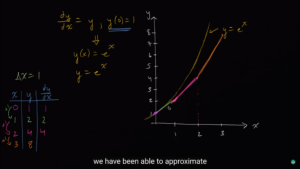
这样我们就使用一条折线(视频中是彩色的线)近似出了那个求不出的微分方程。
我们发现,在上述计算中,我们都使用了[mathjax]\Delta(x)=1[/mathjax]这样的(步长)来近似。如果想算得更精密,完全可以取[mathjax]\Delta(x)=0.5[/mathjax],[mathjax]\Delta(x)=0.25[/mathjax],[mathjax]\Delta(x)=0.01[/mathjax]...
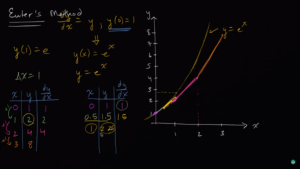
所以计算机就开始拿来计算高精度的浮点数去了。
等等!为什么听起来这么像牛顿法?
确实有点像,但适用场景还是不同的。通常来说牛顿法适用于已知函数,而欧拉法适用于已知微分方程。(它们的目的也不太一样)
| 牛顿法 | 欧拉法 |
| 已知方程,求解一个近似值 | 近似一个亲妈都不认识的微分方程 |
| 比如求解[mathjax]y=x^2-2=0[/mathjax]的近似解[mathjax]\sqrt{2}[/mathjax] | 比如求解[mathjax]y^{\prime}=y,\ y(0)=1[/mathjax]的近似曲线 |
| 需要找一个比较接近的点,然后不断逼近 | 可能需要一个初始点,然后不断画折线 |
| “初始点”越接近目标,总体计算量就越低 | “步长”(在正规欧拉法公式里一半写为[mathjax]h[/mathjax])要一开始就选好,不能中途改 |
| 很多时候“初始点”的选择并不会影响太多计算量(比如求解[mathjax]y=x^2-2=0[/mathjax]的时候选择x=2和x=3区别并不是很大) 或者深度学习训练的时候我们发现一开始的loss无论是20还是30还是50我们都不是很关心,因为很快程序就会开始在loss<0.5的范围缓慢缓慢降低 | 计算量和“步长”的大小相关度很大(比如近似[mathjax]y^{\prime}=y,\ y(0)=1[/mathjax]的时候选择[mathjax]h=1[/mathjax]和[mathjax]h=0.25[/mathjax]计算量差别很大) |
| ...计算量差别不大,因为牛顿法只是想要一个近似解 | ...计算量差别很大,因为欧拉法要近似的是整条曲线 |
一个例子:
🔗 [Square Root of 2, Newton's method vs Euler's method - YouTube] https://www.youtube.com/watch?v=R3G8aJaMngw
快速重新回忆牛顿法:(之前写过笔记,但没认真写完🔗 [2021-10-08 - Truxton's blog] https://truxton2blog.com/2021-10-08/)
来自:🔗 [File:NewtonIteration Ani.gif - Wikimedia Commons] https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif
(下面的gif可能需要点击原图打开)
NP Hard问题(另开笔记)
从这里继续:

NP hard问题
另开一篇笔记...
写完了!🔗 [NP hard相关的话题 - Truxton's blog] https://truxton2blog.com/np-hard-related-topics/
Nonlinear Optimization(就开了个头)
继续:
