This post was published in 2022-09-01. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
今天从哪里开始?
从昨天的笔记的末尾继续:

停!现在准备开始跳跃一些内容。由于差不多理解了傅里叶级数,现在可以试试 连续信号的傅里叶变换 和 离散信号的傅里叶变换 是否能看懂了!
后续更新 :成功了一半。连续信号的傅里叶变换看完了,离散信号的傅里叶变换看完了一半,发现少了一个很重要的地方缺失了:周期离散信号的傅里叶级数如何表示:
P133

(没完全学明白)(非周期信号)连续时间傅里叶变换
笔记1:对非周期信号的一些想法
从P180开始

首先明确几个猜想(自己在学习之前瞎想的,不一定对):
1,只要没有 用明确公式 表示一个无限长的信号,经过傅里叶变换后一定无法100%还原信号的频谱图。 这条结论有点混乱,应该这么说:
假设x(t)=cos(t)对所有t都生效,但我们并不知道这个公式,我们只观察到了一段有限时间内的信号是cos(t),那么用这样一段有限信号得到的频谱图一定有瑕疵,不能得到那种完美的频谱图。
2,上面的第一条猜想对离散、连续信号都是如此。只要无法获取无限长的信号,傅里叶变化后得到的都只能是真实频谱的近似结果。
趁还清醒,整理一下当前的想法:
我发现我很难真正理解P181~P182,或者说P181~P182这两页写的实在是太好了,导致我的笔记没办法做到“更直观易懂”。所以下面贴的笔记只有P181内容的前导。
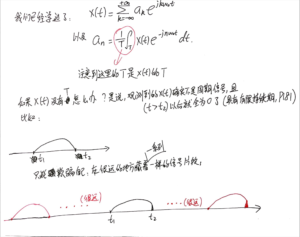

2022-09-03继续在这里写:
我发现我理解不了“越来越密集的采样”的一个主要原因是我无法理解“对连续信号的采样“。
决定先从这里入手,看看能不能更好的理解上面写的内容。
总结:
目前仍然认为有难以理解的地方,由于不想花太多时间,决定跳过了,但是在跳过之前决定把所有有参考价值的东西都写下来。
一段代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 10, num=1000)
y = np.cos(x) / x
xn = np.linspace(1, 10, num=10)
yn = np.cos(xn) / xn
plt.figure()
plt.plot(x, y)
plt.scatter(xn, yn, marker='.', color='red')
plt.show()
xn = np.linspace(1, 10, num=20)
yn = np.cos(xn) / xn
plt.figure()
plt.plot(x, y)
plt.scatter(xn, yn, marker='.', color='green')
plt.show()
xn = np.linspace(2, 20, num=20)
yn = np.cos(1 / 2 * xn) / (1 / 2 * xn)
plt.figure()
plt.plot(x, y)
plt.scatter(1 / 2 * xn, yn, marker='.', color='green')
plt.show()
结果为:
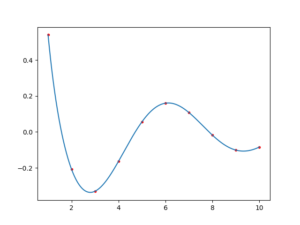
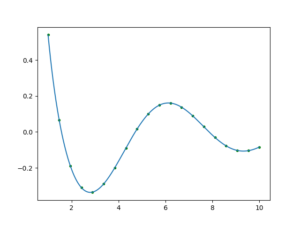
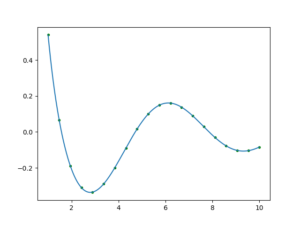
对包络的理解
目前认为最难理解的一部分:
P182
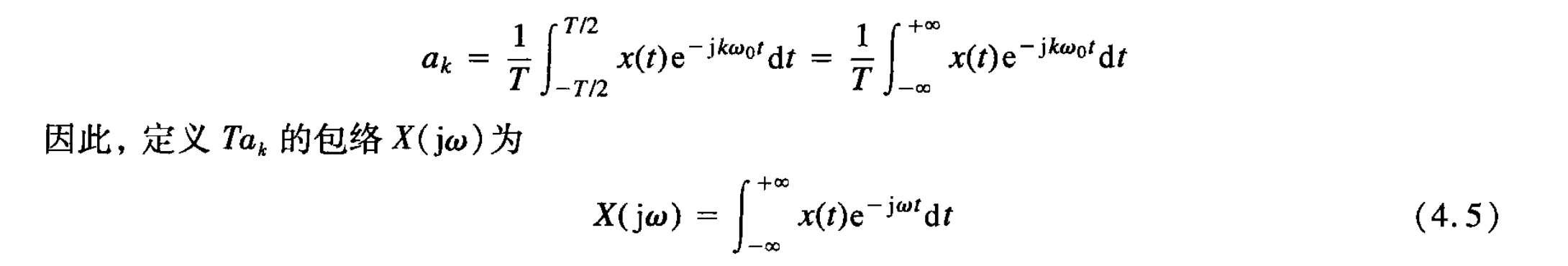
我能够想象得到,随着[mathjax]T[/mathjax]增大,[mathjax]\omega_0[/mathjax]减小,[mathjax]k\omega_0[/mathjax]在坐标轴上越来越“密集”,所以[mathjax]a_k[/mathjax]和[mathjax]k\omega_0[/mathjax]构成的的函数也会越来越“密集”,这样随着[mathjax]\omega_0[/mathjax]无限接近0,原本离散的[mathjax]a_k[/mathjax]会越来越接近连续的[mathjax]a_k[/mathjax] .
但非常恶心的地方在于,我没法用一个数学公式推导出“是的,确实会越来越密集”。
2022-09-17,我尝试补充一点我对这部分内容的理解:

但无论如何,结论还是可以记的:
P182~P183

一些临时的结论
所以说:
一个非常关键的总结写在最前面: 周期信号的复指数信号出现在离散的[mathjax]a_k[/mathjax]上 , 非周期信号的复指数信号出现在连续的[mathjax]a_k[/mathjax]上 . 接下来的内容讨论的范畴基本上也都是非周期信号的(周期信号比较简单,可以直接求的,已经在傅里叶级数的时候就学过了)。
首先我有一个连续信号[mathjax]x(t)[/mathjax];
接下来我要观察一个公式:
[mathjax-d]a_k=\frac{1}{T}\int_{T}x(t)e^{-jk\omega_0 t}dt[/mathjax-d](先不要管那个破包络函数了,我们先理解出频谱图再说)
我的输入信号[mathjax]x(t)[/mathjax]是周期信号吗?(上面这个公式的右半边需要我们提供[mathjax]T[/mathjax])
如果是周期信号,那就直接把[mathjax]T[/mathjax]代入上面公式的右边,得到一系列复指数信号的强度分量[mathjax]a_k[/mathjax]。结束了!这个时候我们得到的是 离散的[mathjax]a_k[/mathjax] . 考虑到某些喜好问题,这里还可以写成[mathjax]a_n[/mathjax],进一步暗示[mathjax]a_n[/mathjax]是离散的数值。
如果不是周期信号,那我们就进行一点小小的欺骗:假设它是周期信号,只是它会在坐标轴很远很远(无限接近[mathjax]\infty[/mathjax])的地方,重复这个信号。从上面的笔记可以得知,[mathjax]T[/mathjax]越大(周期信号重复的地方在非常非常非常远的位置),[mathjax]a_k[/mathjax]的“精度”就越高。但这个时候又出现了另一个问题:[mathjax]T[/mathjax]接近无穷大,[mathjax]\omega_0[/mathjax]接近0,那上面这个[mathjax]a_k[/mathjax]怎么求哦?首先我们要注意一个问题:虽然随着[mathjax]T[/mathjax]不断增大,[mathjax]a_k[/mathjax]会越来越小,但如果用绘图软件进行绘制,不同的[mathjax]T[/mathjax]仅仅会让坐标轴上的数字不同而已。其次要注意这个乘法算式除了一个接近0的[mathjax]\frac{1}{T}[/mathjax],还有一个看起来难以捉摸的[mathjax]\int\limits_{-\infty}^{+\infty}[/mathjax],所以很多时候并不能武断地下结论认为[mathjax]a_k[/mathjax]会“不好求”。(事实上,根据书中P184~P186的各种例题可知,很多拿来分析的包络函数/频谱图[mathjax]X(j\omega)[/mathjax]都是有常数峰值的)。为了避免这个不太愉快的问题,我们干脆把[mathjax]\frac{1}{T}[/mathjax]去掉,只拿[mathjax]{\color{red}{X}}(j\omega t)=\int\limits_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt[/mathjax](这就是所谓的包络函数)出来当作频谱图! 这部分笔记有点问题,建议参考本笔记上面补充的这张图。T越来越接近无穷大并不是什么问题,因为我们要探究的是各频率之间的相对关系,而不是强度分量的绝对数值。随便找一张频谱图为例,我们对频谱图的y轴上的绝对数值大小并不感兴趣,我们只对频谱图的形状感兴趣。
此外,由于[mathjax]\omega_0[/mathjax]越来越接近0,由包络函数反推回[mathjax]x(t)[/mathjax]的表达式也发生了变化:(注意下面红色的[mathjax]\color{red}X[/mathjax]代表的是包络函数)
[mathjax-d]x(t)=\sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0 t}=\sum_{k=-\infty}^{+\infty}\frac{1}{T}{\color{red}{X}}(jk\omega_0)e^{jk\omega_0 t}=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\color{red}{X}}(j\omega)e^{j\omega t}d\omega[/mathjax-d]一些例题
非周期连续信号的傅里叶变换
接下来做3道例题,加强一下印象:
P184~P186,这些都是非周期连续信号的傅里叶变换。



周期信号的傅里叶级数
以及周期函数的傅里叶变换:
P188
备注:该题的巧妙观察解法也补充在了下面(写在Dirac delta function的后面)
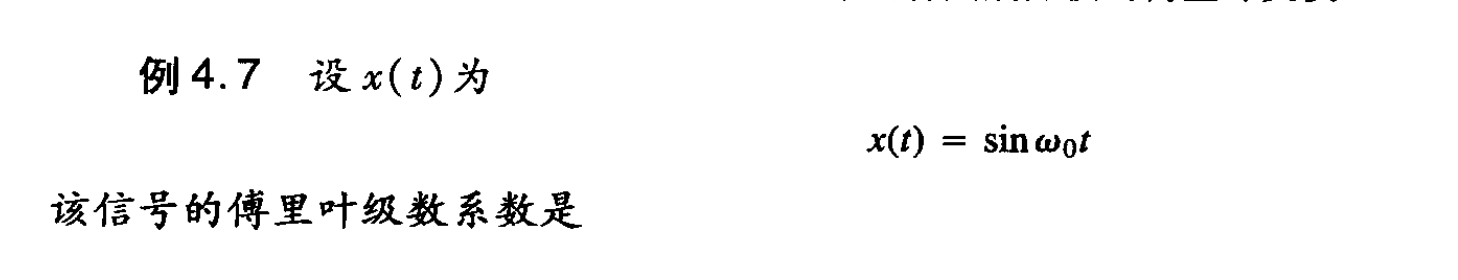
遇到麻烦了!Dirac delta function. 中文称为 狄拉克δ函数 .
参考资料:
🔗 [Fourier transform of sin(x) - Wolfram|Alpha] https://www.wolframalpha.com/input/?i=Fourier+transform+of+sin(x)
🔗 [Dirac delta function - Wikipedia] https://en.wikipedia.org/wiki/Dirac_delta_function
🔗 [Fourier Transform of Basic Signals (Sinω₀t) - YouTube] https://www.youtube.com/watch?v=c9zCIPsH4R4

算了算了,暂时不搞了。
反正短期内也用不上,不如赶紧继续学离散傅里叶变换吧。
停!
事实上,狡猾的奥本海姆在P120,学习周期信号的傅里叶级数的时候早已暗示了另一种“观察可得”的方法,只是他没有明说常规“硬算”的Dirac delta方法比较难。
