2022-10-01

WARNING: This article may be obsolete
This post was published in 2022-10-01. Obviously, expired content is less useful to users if it has already pasted its expiration date.

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

狄拉克函数 / Dirac Delta Function

解决之前遗留的问题：Dirac delta function

解决之前遗留的问题：Dirac delta function

上一次出现：🔗 2022-09-01

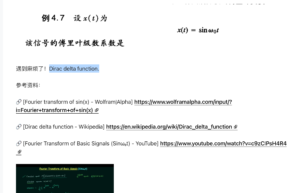
回顾之前涉及狄拉克函数的笔记

可能是有一段时间没做信号与系统的题了，我的脑子出了问题，把这部分内容的答案记错了：

现在先试着用常规的周期连续傅里叶公式来分析[mathjax]x(t)=\sin(\omega_0 t)[/mathjax]：

其实完全没有推导难度，只是我记错了[mathjax]e^{j2\pi n}[/mathjax]的值，浪费了很长时间，感到非常气愤：

接下来的内容出了点小问题，为了不耽误时间，新开了一篇草稿等待后续处理：

（2023年还没搞定，不搞了）🔗 [sin(wt)不使用狄拉克函数计算傅里叶变换 - Truxton's blog] p=9507

狄拉克函数的基础内容学习

先不管之前计算的那些东西了，先搞点实在的公式：

（当然还是要从之前的笔记开始：这张图）

这个物理过程（远超安全阈值的电流在极短的时间内流过人体，但雷击的总能量是有限的）也可以帮助理解这个函数的性质：

该怎么描述呢...首先 狄拉克函数 就是 冲激函数 ！

接下来在信号系统的范畴内（可能并不绝对严谨地）列举一些重要的表达式：

然后是一些常见公式的相关推导：

上面的2张手写笔记可能需要用到这个公式（尽管信号是周期信号，但这个公式依然可以用）：

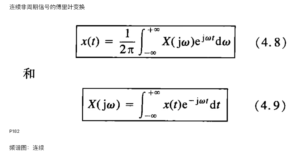
挺好，这点东西就是目前接触过的所有关于狄拉克函数的内容了。除非遇到更进一步的信号系统题，否则狄拉克函数就先学到这里吧。