This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今天从哪里开始？
从昨天的内容继续学！
冲激响应 / 脉冲 / 单位阶跃
P23
先考虑离散信号
单位脉冲：
[mathjax-d]\delta[n]= \begin{cases}0, & n \neq 0 \\ 1, & n=0\end{cases}[/mathjax-d]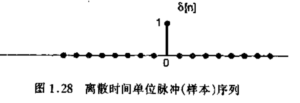
单位阶跃：
[mathjax-d]\mu[n]= \begin{cases}0, & n < 0 \\ 1, & n\geq 0\end{cases}[/mathjax-d]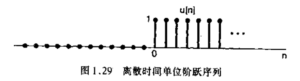
一些关系：
接下来部分内容比较搞人心态，主要原因是：单个公式的推导难度极低（不需要什么数学知识），但组合在一起就变成了一坨不好理解的东西（书本后面有）。
目前能做的就是：找一张草稿纸从头到尾把这些公式都 推导、画图 复习一遍。
唯一需要特别注意的是一个新概念： 延时冲激 ：
[mathjax]n=0[/mathjax]时发生的[mathjax]\delta[n][/mathjax]；[mathjax]n=1[/mathjax]时发生的[mathjax]\delta[n-1][/mathjax]；[mathjax]n=2[/mathjax]时发生的[mathjax]\delta[n-2][/mathjax]；...
下面是P23~P24的完整页面备份：
连续信号的单位脉冲和单位阶跃暂时先不学了。P24~P27
信号系统的一些基本分类与性质（主要为了介绍LTI系统）
下面是系统的一些基本性质（书本P32开始），仅截出概念定义的部分：
记忆与无记忆系统
可逆性与可逆系统
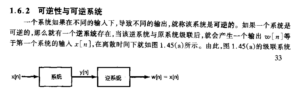
因果性
稳定性
另一个不错的例子是“把扩音喇叭的输出口接到输入口形成一个闭环”，此时系统是不稳定的，因为信号会不断放大放大
时不变性
线性
学完了。赶紧开始学 第二章：线性时不变系统。
LTI系统、脉冲、卷积
线性时不变系统：简写为 LTI系统 .
例题（书P56）：用单位脉冲信号[mathjax]\delta(n)[/mathjax]的方法“分解”这个离散信号：
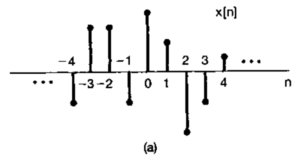
答案
[mathjax-d]\begin{aligned}x[n]=\ldots &+x[-3] \delta[n+3]+x[-2] \delta[n+2] \\ &+x[-1] \delta[n+1]+x[0] \delta[n] \\ &+x[1] \delta[n-1]+x[2] \delta[n-2] \\ &+x[3] \delta[n-3]+\ldots \end{aligned}[/mathjax-d]
所以可以得出这个一般化的“分解”公式：
[mathjax-d]x[n]=\sum_{k=-\infty}^{+\infty}x[k]\delta[n-k][/mathjax-d]接下来理解P57的这个：
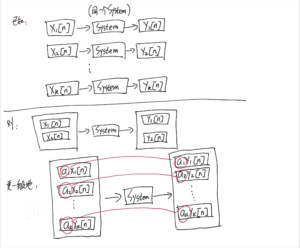
在本笔记的前面，学习 线性系统的叠加性 的时候写过这张草稿：
现在继续：
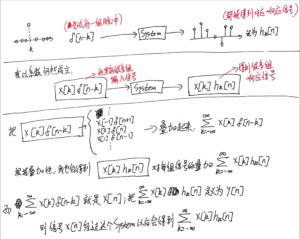
所以就可以理解[mathjax]y[n]=\sum\limits_{k=-\infty}^{\infty}x[k]h_k[n][/mathjax]了！再次引用P57的结论：
如果已知一个线性系统对每一个移动单位脉冲序列的响应，则系统对任何输入的响应都可以求出。
信号与系统P57
注意上面quote的红字，要实现对一个线性系统的彻底了解，红字的内容是工作量最大的：要收集每一个移动单位脉冲的响应的数据！
如果此时，线性系统变成了 线性时不变系统LTI ，那么工作量就小很多很多了，只需要收集任意一个移动单位脉冲的响应数据，就可以推算出其他所有移动单位脉冲的响应数据！
现在把[mathjax]h_0[n][/mathjax]简写为[mathjax]h[n][/mathjax]，我们可以得到：
[mathjax-d]y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k][/mathjax-d]上面的公式可以理解为：
首先我掌握了一条可以反复利用的重要数据：系统对单位脉冲信号[mathjax]\delta[n][/mathjax]的响应[mathjax]h[n][/mathjax] . 有了这个数据以后，这个系统对任何时间偏移的脉冲序列的响应都是可以推算出来的：把[mathjax]h[n][/mathjax]平移到对应偏移的位置就可以！比如现在我们要计算单位脉冲信号[mathjax]\delta[n+30][/mathjax]的响应，我们只需要把[mathjax]h[n][/mathjax]的信号向左平移30单位就可以，也就是[mathjax]h[n+30][/mathjax]. 有了上面的这套万金油平移法则以后，我们再对每一套偏移响应[mathjax]h[n+k][/mathjax]乘上一个对应的分量[mathjax]x[k][/mathjax]就可以了！最后我们把上面这些结果全部加起来（k遍历所有偏移量），就可以得到系统对信号[mathjax]x[n][/mathjax]的响应[mathjax]y[n][/mathjax] .
卷积和
[mathjax-d]y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k][/mathjax-d]定义卷积运算符号[mathjax]*[/mathjax]，上面这个公式可以写成卷积和的形式：
[mathjax-d]y[n]=x[n]*h[n][/mathjax-d]用卷积的风格来描述上面的2个公式：
取输入信号的每一个“点”，把万能脉冲响应信号拉过来（拉到这个“点”对应的时间偏移位置）相乘，得到一组时序数据；把每一个“点”对应的时序数据叠加起来就产生了系统的响应信号。
Example：
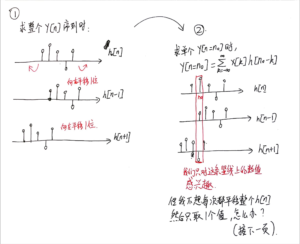
观察上面的卷积和公式：
[mathjax-d]y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k][/mathjax-d]注意到[mathjax]n[/mathjax]也是要取[mathjax]-\infty \rightarrow +\infty[/mathjax]的，这意味着我们在计算完整[mathjax]y[n][/mathjax]的时候需要处理2个大循环。可以想像有一种方法是分别求[mathjax]y[1], y[2], y[3] \cdots[/mathjax]的值，然后构成完整的[mathjax]y[n][/mathjax]；还有一种方法是分别求[mathjax]k=1, k=2, k=3 \cdots[/mathjax]对应的[mathjax]y_k [n][/mathjax]，然后把它们叠加起来：
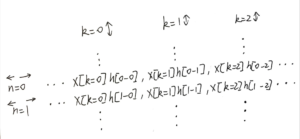
如果我要单独求[mathjax]y[n][/mathjax]上某个时刻的数值（而不是整个[mathjax]y[n][/mathjax]），应该怎么办？其实还是沿用之前的方法，只是我们并不需要计算并叠加“整条信号”了：
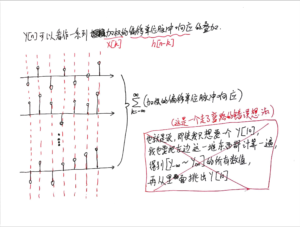
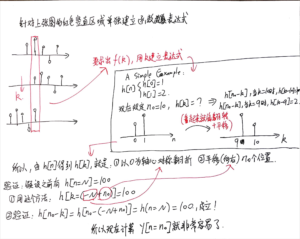
接下来要通过一些例题巩固自己对 离散信号的卷积 的想象。
信号与系统这本书的很多例题总是不把题目的要求明确说出来，所以这道题要询问我们的应该是：
分析输出信号y[n]的表达式。
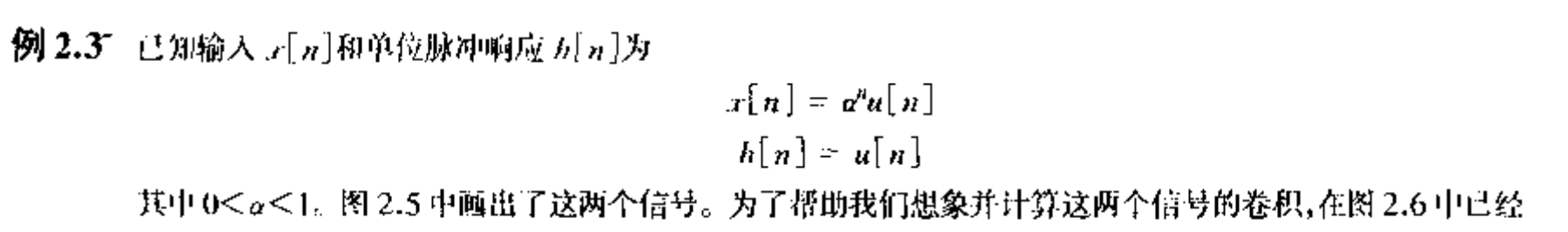
下面是一些草稿。这种题目一开始做的时候很容易陷入“条件判断太多”的烦躁情绪，所以一个非常有用的环节就是“先把所有可能列举的信号图都画出来，然后堆叠在一起进行观察”。
下面的草稿里会有到等比数列的求和：见以前写过的笔记
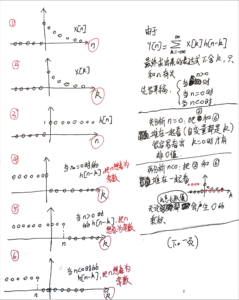
有关离散信号的卷积还有更多的题，暂时先不做了。
