WARNING: This article may be obsoleteThis post was published in 2022-10-08. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
（实际上并没有按计划学习的学习计划）离散信号下的傅里叶变换性质
* 注：在整理这篇笔记的时候发现，下面写的这个学习计划并没有实际学习，可能是因为有点难，前置工作太多。
尝试学习以下话题：
（离散信号下的）傅里叶变换，滤波器，卷积性质
（复习）卷积，滤波
先学习这些内容：卷积，滤波
复习老笔记：🔗 2022-08-28 ；🔗 2022-08-29 .
连续傅里叶级数的性质
（以前应该没有学过）P127，连续傅里叶级数的性质
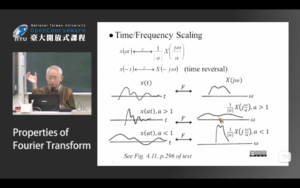
信号在时域和频域的表达
补充一张图：
related: 🔗 [Ch3_FourTrans&DeltaFns.pdf] https://www.ldeo.columbia.edu/~richards/webpage_rev_Jan06/Ch3_FourTrans%26DeltaFns.pdf
如何求Dirac Delta Function的傅里叶级数呢？
[mathjax-d]\delta(x) \xRightarrow{\mathcal{F}}?[/mathjax-d]事实上应该非常简单。造成疑惑的主要原因是我把上面这张图表达的含义看错了，误以为Dirac delta function的傅里叶变换应该得到某种复指数曲线。
实际上应该是：
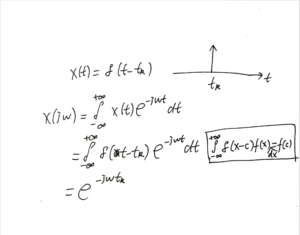
所以，对[mathjax]x(t)=\delta(x)[/mathjax]而言，[mathjax]\delta(x) \xRightarrow{\mathcal{F}}\ 1[/mathjax]
线性性质
线性性质
时移性质
时移性质
但是在这部分出现了理解问题：明明[mathjax]b_k=e^{-jk\omega_0 t_0}a_k[/mathjax]，为什么还会得出结论说[mathjax]\left| a_k\right|=\left| b_k \right|[/mathjax]呢？
好像明白了。不知道为什么会对这种问题感到迷惑，可能是因为对复指数的模长想象错了：
[mathjax-d]\text{Mod}(e^{jk\omega_0 t_0})=1[/mathjax-d]所以说模长确实是不变的。
见https://www.bilibili.com/video/BV1dM4y1M7LK?p=10，(p10)43分钟左右
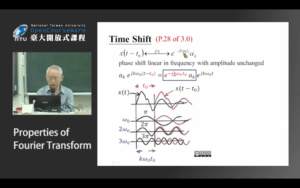
注意：对一个复指数信号[mathjax]x(t)=e^{jk\omega_0 t}[/mathjax]，如果对它乘上一个[mathjax]e^{-jk\omega_0 t_0}[/mathjax]，变成了[mathjax]e^{-jk\omega_0 t_0}x(t)[/mathjax]，那么它会发生什么变化呢？
答案： 会发生时移 ，仅仅是在时间轴上平移了一段距离！
所以正如上面这张图所示，信号平移 = 一系列复指数信号平移 = 一系列复指数的Magnitude不变。
或者说，当一个信号时移了[mathjax]t_0[/mathjax]以后，它的所有傅里叶级数信号都会做相同的[mathjax]t_0[/mathjax]时移。（注意这里的[mathjax]t_0[/mathjax]不仅有大小还有方向）
如何改变傅里叶级数的模长
在上面一部分我们可以知道，信号的时移无法改变傅里叶级数的模长。那什么情况下能改变傅里叶级数的模长呢？
显然我们知道[mathjax]x(t)\rightarrow x(at)[/mathjax]这样的变换是可以改变的。但我们怎么用公式严谨地推导出来呢？
同时参考
以及还可以参考BV1dM4y1M7LK p11 25:10左右开始
