2022-09-16 - Truxton's blog

WARNING: This article may be obsolete
This post was published in 2022-09-16. Obviously, expired content is less useful to users if it has already pasted its expiration date.

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

Table of Contents

今天从哪里开始？

今天从这里开始：

奥本海姆信号与系统P331 第7章采样

总结主要内容

学习了采样定理的一点表皮知识；学习了人耳听觉频率和实际声音信号频率的关系；学习了“频率随时间变化”的信号的表达方式。

信号与系统：采样定理（根本没学进去）

P331 采样定理的学习范畴

接下来学习P332的这一部分内容，是理解香农采样定理的核心部分：

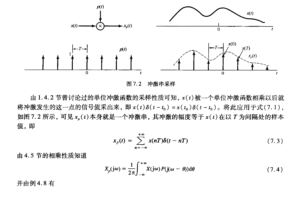
首先要复习一下很久没看的冲激、卷积，为此把08-28的笔记放出来了：🔗 [2022-08-28 - Truxton's blog] https://truxton2blog.com/2022-08-28/

前置知识要求有点多，先从这里开始：

P199

这部分内容需要熟悉非周期傅里叶变换的推导（包络函数那一块的内容）

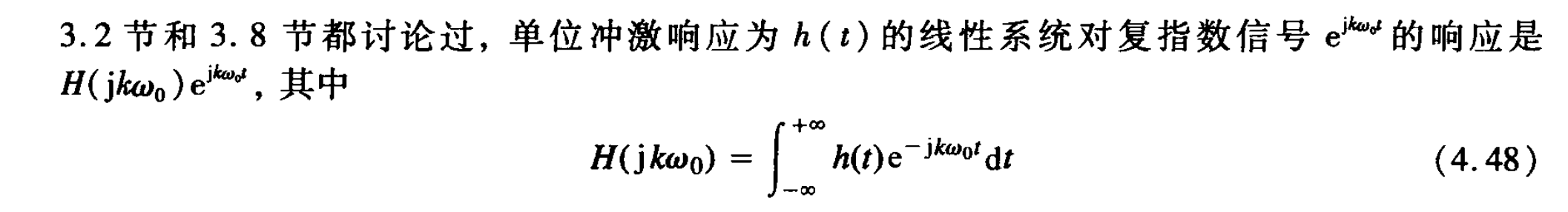
这部分内容需要熟悉2022-08-29的笔记：

* 截图的时候2022-08-29还是未发表的草稿，所以实际笔记的排版和截图可能有所不同

注意到被积变量是可以替换的，也就是说我们熟悉的：

[mathjax-d]y(t)=e^{jk\omega_0 t}\int_{-\infty}^{+\infty}h(\tau)e^{-jk\omega_0 \tau}d\tau[/mathjax-d]

和P199出现的

[mathjax-d]y(t)=e^{jk\omega_0 t}\int_{-\infty}^{+\infty}h(t)e^{-jk\omega_0 t}dt[/mathjax-d]

是一个东西！

所以现在P199的这部分内容就可以理解了。

然后看这里：

公式（3.121）在P144：

而公式（3.124）在P145：

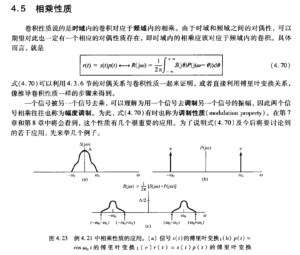
然后再看一下P205的相乘性质：

人耳听觉频率和声音信号频率的关系

* 以下内容默认：所有听觉频率均在人耳识别范围内。

暂停一下，（学不下去了），现在转入一个比较简单的话题：

如果我有一台声音录制设备，它的采样频率固定为[mathjax]F_s[/mathjax]，现在我要用这台录音设备采集[mathjax]0\sim +\infty[/mathjax]频率的声音信号，会录制出什么结果呢？

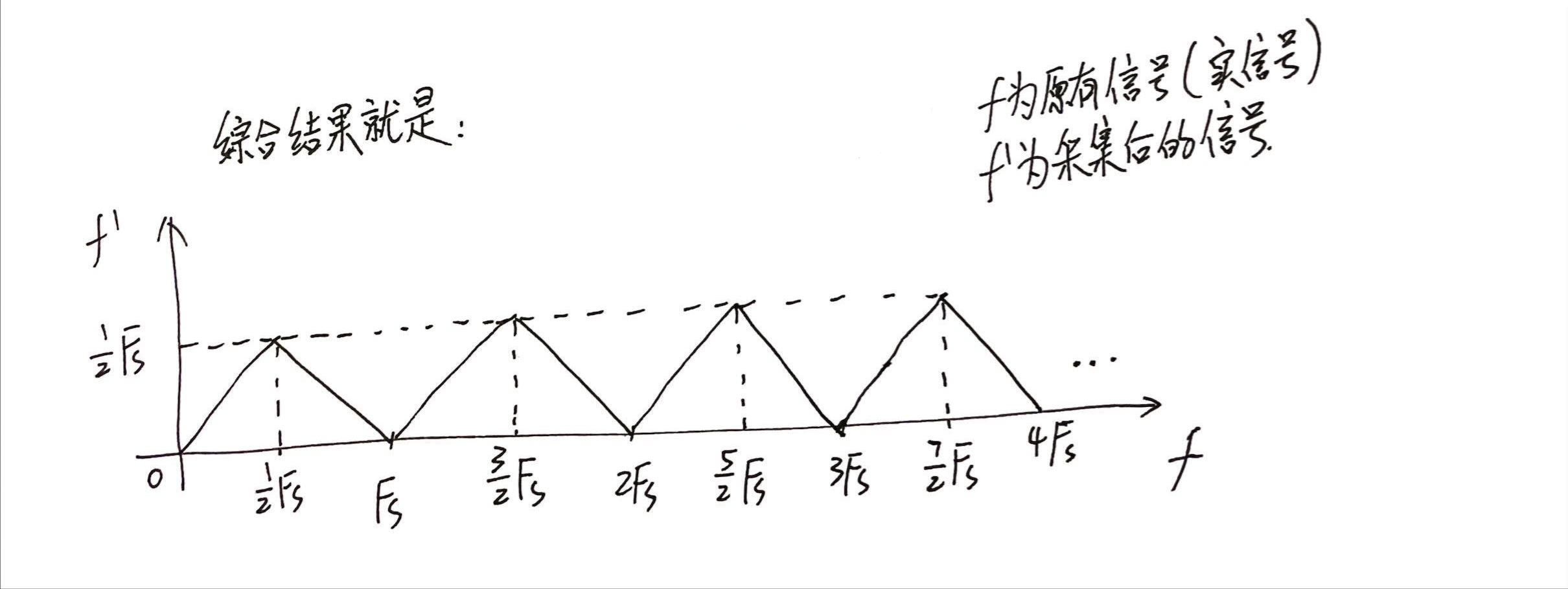
分析结果如下：

频率随时间变化的信号

Chirp/啁啾信号

以chirp为例，在信号与系统P415：

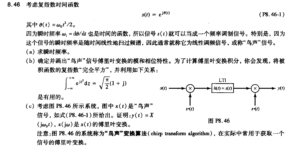
这里给出了chirp信号的表达式：

[mathjax-d]s(t)=e^{j\frac{\omega_0 t^2}{2}}[/mathjax-d]

现在的问题是：如何理解这个信号的表达式？chirp信号的频率和时间的关系是什么？

如果只是单纯的这样理解：

[mathjax-d]s(t)=e^{j\frac{\omega_0 t^2}{2}}=e^{j\frac{\omega_0 t}{2}t}[/mathjax-d]

就会得到错误的结果[mathjax]\color{red}{\omega=\frac{1}{2}\omega_0 t}[/mathjax]. 此时我们可能会大为疑惑，这个奇怪的1/2是这么回事？为什么不是1或者1/3, 1/4 ... ？

类比一下初中物理学过的匀速运动、匀加速运动：

如果匀速运动，则有[mathjax]S=vt[/mathjax]；

但如果有均匀加速[mathjax]V(t)=t[/mathjax]，则有[mathjax]S=\frac{1}{2}vt^2=\frac{1}{2}t^2[/mathjax]，而不是把[mathjax]V(t)=t[/mathjax]直接代入到[mathjax]S=vt[/mathjax]中进行计算。

复指数信号也是一样。为什么有[mathjax]x(t)=e^{j\omega t}[/mathjax]？因为这里假设的是复平面上的点正在匀速绕圈！

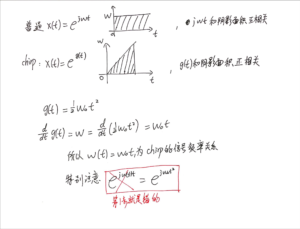
最后总结一点经验公式：

上面的解法都是解析解，也就是说我们可以求出[mathjax]\int_{0}^{t}f(\tau)d\tau[/mathjax]的表达式。如果我们不能求出这个积分的解析解，也可以通过微积分的基本定义来近似，这个方法在写程序的时候经常用到，因为绝大多数场合下我们写的程序都是“采样足够密集，可以近似当成连续信号的离散信号”。

下面的R程序使用了2种不同的方法来生成chirp：

library(tuneR)

# 方法1: 直接用g(t)积分求得的解析解
# 在3秒内，从f=300Hz线性增加到f=420Hz
# f=300+40t
# g(t)=2pi*(300t+20t^2)
# x(t)=cos(g(t))
Fs = 44100
t = seq(0, 3, by = 1 / Fs)
xt1 = cos(2 * pi * (300 * t + 20 * (t ^ 2)))

bits = 16
wave1 = floor(2 ^ (bits - 1) * xt1)
wave1 = as.integer((wave1 - min(wave1)) / (max(wave1) - min(wave1)) * (32767 +
                                                                         32768) - 32768)
wave_stereo1 <- cbind(wave1, wave1)
writeWave(Wave(wave_stereo1, samp.rate = Fs, bit = bits),'./chirp1.wav')   



# 方法2:
# 现在假设我不知道g(t)的解析解
# 只知道f=300+40t
# g(t)可以表达为2pi*(Δ*f(Δ)+Δ*f(2Δ)+Δ*f(3Δ)+...), Δ->0
# x(t=1)就是cos(2pi*(Δ*f(Δ))), x(t=2)就是cos(2pi*(Δ*f(Δ)+Δ*f(2Δ))),
# x(t=3)就是cos(2pi*(Δ*f(Δ)+Δ*f(2Δ)+Δ*f(3Δ))) ...
# 以此类推
delta = 1 / Fs
delta_series = seq(0, 3, by = 1 / Fs)
f_delta_series = 300 + 40 * delta_series
g_t = 2 * pi * cumsum(delta * f_delta_series) # 千万不要写成了cumsum(delta_series*f_delta_series)
xt2 =  cos(g_t)

#plot(f_delta_series)

bits = 16
wave2 = floor(2 ^ (bits - 1) * xt2)
wave2 = as.integer((wave2 - min(wave2)) / (max(wave2) - min(wave2)) * (32767 +
                                                                         32768) - 32768)
wave_stereo2 <- cbind(wave2, wave2)
writeWave(Wave(wave_stereo2, samp.rate = Fs, bit = bits),'./chirp2.wav')

生成的chirp wave file（两种方法生成的文件听起来应该是一样的）：

Vibrato/颤音

这部分内容是2024年2月补充的，已经1年没摸过相关内容了，连欧拉公式都快忘了，所以这部分笔记还包含相当一部分音频信号复健学习：

颤音/Vibrato，简化版的音频信号大概可以理解成这样的：

我们当然会生成一段普通的440Hz的音频信号，频谱图是一条直线（y=440Hz），意味着频率固定为440Hz
如果这个频率并不固定在440Hz，而是在440Hz上下波动；更确切地说，以正弦信号的方式在440Hz的基准线上下波动10Hz。这个时候我们就得到了最简单的Vibrato音频。

直接从欧拉公式开始复健：

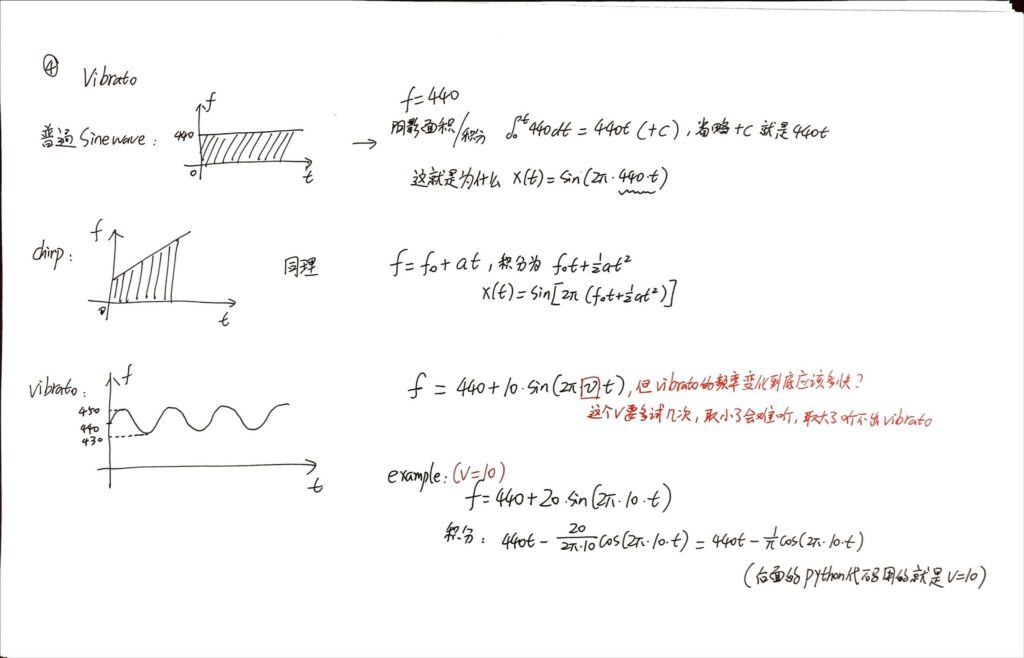
代码如下：

import numpy as np
from scipy.io import wavfile

bits = 16
sr = 44100


def save_wav(y, filename):
    # Scale the signal to fit the desired bit depth range
    y_scaled = np.int16(y * (2 ** (bits - 1) - 1))
    # Save the wav file
    wavfile.write(filename, sr, y_scaled)


if __name__ == '__main__':
    t = np.linspace(0, 10, 10 * sr)

    # 先生成一段440Hz的sinewave熟悉一下代码
    y = np.sin(2 * np.pi * (440 * t))
    save_wav(y, '440_sinewave.wav')

    # 使用vibrato的解析解
    y = np.sin(2 * np.pi * (440 * t - 1 / (1 * np.pi) * np.cos(2 * np.pi * 10 * t)))
    save_wav(y, 'vibrato_v1.wav')

    # 使用vibrato的积分
    # 具体思路参考先前chirp R code的注释
    delta = 1 / sr
    delta_series = np.arange(0, 10, 1 / sr)
    f_delta_series = 440 + 20 * np.sin(2 * np.pi * 10 * delta_series)
    g_t = 2 * np.pi * np.cumsum(delta * f_delta_series)
    y = np.sin(g_t)
    save_wav(y, 'vibrato_v2.wav')

生成的音频：

440_sinewav.wav是最普通的440Hz sinewave：

然后是2个（理论上一样）的vibrato，以440Hz为基准上下浮动20Hz，变动速率为10Hz

上面这两段Vibrato的频谱图：

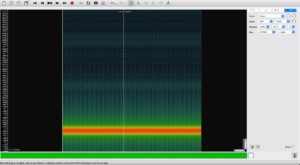
注意：上面这张频谱图看起来波动范围有点大了，不像是440±20Hz，其实是window size的问题，把window size拉到最大就可以了：

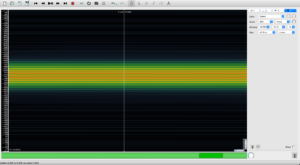
上面的vibrato例子听起来并不是那么像音乐演奏的颤音，可以把10Hz变动速率变高一点，上下浮动变为10Hz

核心代码：

# 使用vibrato的解析解
y = np.sin(2 * np.pi * (440 * t - 1 / (1 * np.pi) * np.cos(2 * np.pi * 10 * t)))

这次听起来更像vibrato一点：

失败的Vibrato音频：越来越高的频率

假如我们不按照求积分的方法做Vibrato，而是直接把[mathjax]f(t)=440+10\sin(2\pi\cdot 10\cdot t)[/mathjax]代入[mathjax]x(t)=\sin(2\pi\cdot f(t)\cdot t)[/mathjax]里面去，得到（错误的）：

[mathjax-d]x(t)=\sin[2\pi (440+10\sin(2\pi\cdot 10 t))\cdot t][/mathjax-d]

就会生成一段难以置信的音频：

注意耳朵

这不应该！我的函数似乎只是围绕着440Hz上下浮动，为什么会产生这么高的频率？

事实就是如此。如果进行频率分析（求导），可以发现频率越到后面越大

代码（为了保护耳朵，这里限制了4秒的音频，因为越到后面声音越尖）

import numpy as np
from scipy.io import wavfile

bits = 16
sr = 44100


def save_wav(y, filename):
    # Scale the signal to fit the desired bit depth range
    y_scaled = np.int16(y * (2 ** (bits - 1) - 1))
    # Save the wav file
    wavfile.write(filename, sr, y_scaled)


if __name__ == '__main__':
    t = np.linspace(0, 4, 4 * sr)

    y = np.sin(2 * np.pi * (440 + 10 * np.sin(2 * np.pi * 10 * t)) * t)
    save_wav(y, 'whattttttttt.wav')

这里展示一下10秒音频（把代码里的t = np.linspace(0, 4, 4 * sr)修改为10即可）的频谱图：

Last Modified in 2024-02-28