WARNING: This article may be obsoleteThis post was published in 2022-08-27. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
本笔记的基本内容
前半部分：尝试学习NTU李琳山的公开课P1~P2；
后半部分：发现NTU的公开课看不懂，所以开始看奥本海姆《信号与系统》
今天从哪里开始？
继续2022-08-25的笔记，
在2022-08-25的笔记中写了这些内容：
继2022-06-09（三角函数和正弦波的基础基础知识）以后，复习了极坐标、复数，推导了欧拉公式（不算严格证明），并学习理解了复数波这个概念。
NTU公开课：李琳山 信号与系统
目录
从这里开始：https://www.bilibili.com/video/BV1dM4y1M7LK
目录：
（似乎）在学习Fourier之前还有一些东西要了解，比如 线性时不变系统 .
P2
P2
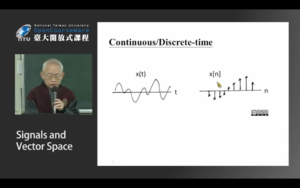
（上一张图）：信号的变换（transformation），需要注意的是图片里的问号 ？ 就目前来说代表的含义是“不能像连续信号那样直接进行计算（要用别的更复杂的方法）”。
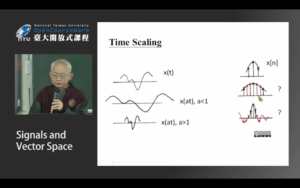
对上一张图片的补充解释。比如车轮辐条的人眼观察、直升机螺旋桨的人眼观察。
所以说，对于discrete signal而言，一般来说：
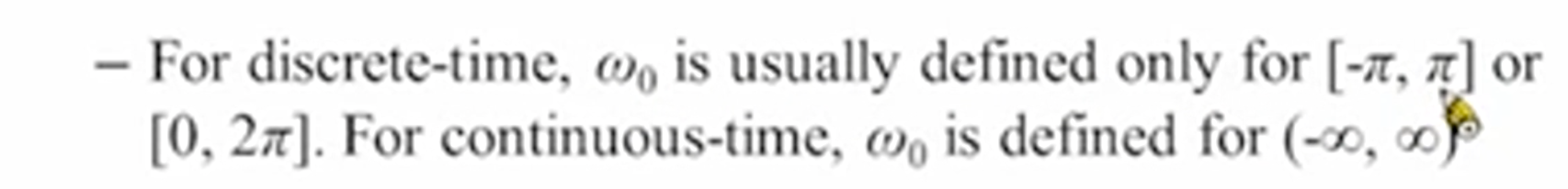
那么如何判断一个discrete signal是否有周期呢？
下面举了3个例子：
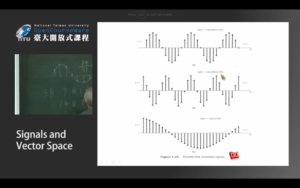
对这三张图的计算：
接下来学习脉冲/impulse：
首先考虑模拟信号：
先想象一下我们有下图所示的2种信号，可以把左边的图看作一个信号（横轴为时间），右边的图是左边的信号的“斜率”。
如果把上图的[mathjax]\Delta t[/mathjax]认为是无限接近于0的，那么理想情况下就变成了：
它们的定义如下：
暂时不知道它们的作用。先继续学习离散信号的unit impulse：
impulse和step function的作用之一：
最后学习系统（这玩意怎么看上去和滤波器是一个东西？当然事实上不是一个东西，因为它拥有很多性质，比如：性质1，性质2 ... 等等，其中还有已经学过的熟悉名词： 线性时不变（系统） ）
P3
P3
要理解P3的内容，需要理解（离散）卷积的含义。下面先粘贴一些视频截图，然后慢慢进行增删：
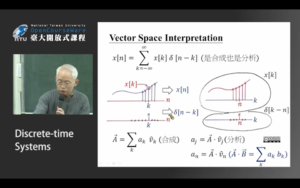
下面这张图讲述了一个具体应用：
现在假设我有一个system S（time-invariant和linear的），我如何用抽象这个系统的功能？对这个系统而言，输入x1会得到y1，输入x2会得到y2，输入x3会得到y3...我当然不能把它们都列举完毕，用来描述这个系统。我可以使用一个[mathjax]\delta(n)[/mathjax]作为输入，经过系统处理后得到输出。这样我就可以用上面这个行为来描述整个系统了，因为在之前几张笔记图片里提到过，（对于time-invariant和linear的系统）可以任何信号都可以用[mathjax]\delta(n)[/mathjax]来表示。（[mathjax]\delta(n)[/mathjax]就是那个“除了n=0的地方为1，其余地方都为0”的信号）
总结：
暂停
学到这里发现不太会了（为什么学不会？因为这个公开课参考的是奥本海姆的《信号与系统》）。决定另找教程再理解：
奥本海姆 信号与系统
连续信号的几种表示方法
对于一个周期信号，取最小正值周期另定义为 基波周期 ，写为[mathjax]N_0[/mathjax]或[mathjax]T_0[/mathjax]：
同时我们还可以定义 基波频率 ，写为[mathjax]\omega_0[/mathjax]. （这部分在书P13）
信号与系统P12
连续时间复指数信号写为：
[mathjax-d]x(t)=Ce^{at}[/mathjax-d]其中[mathjax]C[/mathjax]和[mathjax]a[/mathjax]可以为实数或者复数。
[mathjax-d]x(t)=Ce^{at}[/mathjax-d]
实指数信号：[mathjax]C[/mathjax]和[mathjax]a[/mathjax]都为实数。就是普通的自然衰减曲线。略过。
[mathjax-d]x(t)=Ce^{at}[/mathjax-d]
周期复指数信号：[mathjax]C[/mathjax]为实数，[mathjax]a[/mathjax]为纯虚数。特别考虑信号：[mathjax]x(t)=e^{j\omega_0 t}[/mathjax]进行额外分析：
它有一个重要性质：无论[mathjax]\omega_0[/mathjax]如何取值，这个信号都是周期信号。当[mathjax]\omega_0\neq 0[/mathjax]时，这个信号的基波周期[mathjax]T_0[/mathjax]为：[mathjax]T_0=\frac{2\pi}{\left| \omega_0 \right|}[/mathjax]. 基本推导如下（这里暂时不对[mathjax]\omega_0[/mathjax]或[mathjax]\left| \omega_0 \right|[/mathjax]进行太多区分，仅在最后一步加上绝对值符号）
正弦信号：[mathjax]x(t)=A\cos(\omega_0 t+\phi)[/mathjax]. 它的基波周期为[mathjax]T_0=\frac{2\pi}{\omega_0}[/mathjax].
接下来是一些 复指数信号与正弦信号的转换关系 ，这里仅截图：
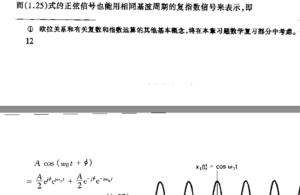
接下来就是对复指数信号Energy和Power推导：
看来还是前两天的笔记不够细心，现在补充在2022-08-25.
更多计算可见：🔗 [12] https://matel.p.lodz.pl/wee/i12zet/Signal energy and power.pdf，但暂时不在今天的笔记里学习。
组成谐波关系的复指数信号
啊，非常熟悉，和之前学过的 harmonic series 一样。
例题：求下面信号的模：（来自信号与系统P14）
[mathjax-d]x(t)=e^{j2t}+e^{e3t}[/mathjax-d]答案
（相关笔记也写在了2022-08-25）
一般复数信号
[mathjax-d]x(t)=Ce^{at}[/mathjax-d]在之前的笔记里，如果[mathjax]a[/mathjax]是纯虚数，[mathjax]C[/mathjax]是实数（或者干脆取[mathjax]C=1[/mathjax]），那就是熟悉的、一定是周期信号的 复指数信号：[mathjax]x(t)=e^{j\omega_0 t}[/mathjax].
由于纯虚数也是复数的一种，纯实数也是复数的一种，现在就考虑更一般的形式：
如果[mathjax]a[/mathjax]不是纯虚数，是复数（写成[mathjax]a+bi[/mathjax]的形式）；而C也是复数，写成极坐标的形式，那么：
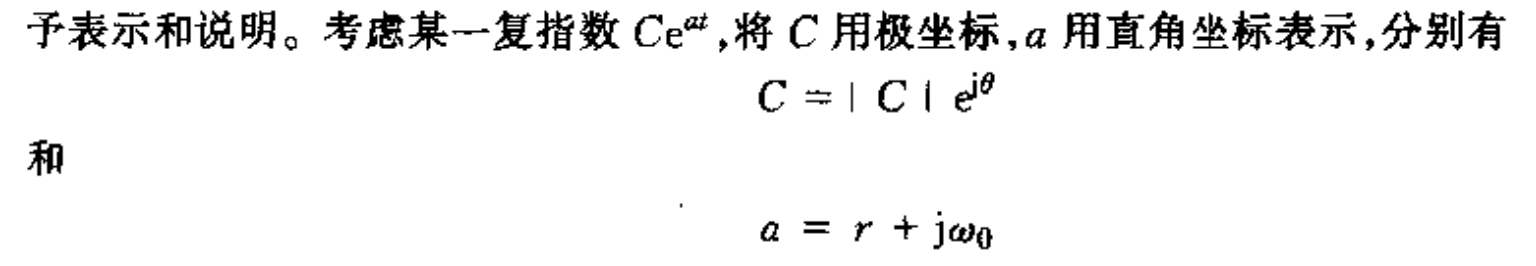
这个时候信号就可以写为：
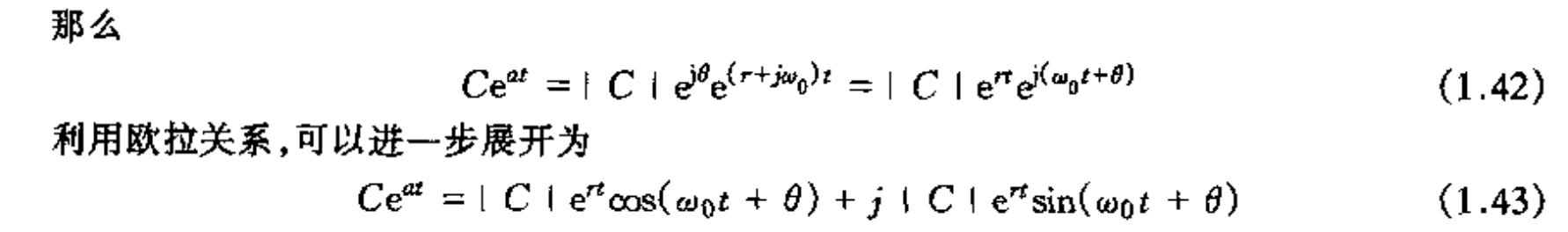
把图片里的公式用Mathjax重写一遍：
[mathjax-d]C e^{a t}=|C| \mathrm{e}^{r t} \cos \left(\omega_{0} t+\theta\right)+j|C| \mathrm{e}^{r t} \sin \left(\omega_{0} t+\theta\right)[/mathjax-d]注意到这个信号是之前学过的[mathjax]x(t)=e^{j\omega_0 t}[/mathjax]信号的 一般形式 ，所以当然，一般形式可以转换为特殊形式：取C=1（不含虚部的极坐标）和r=0（复数转换为纯虚数）就可以得到。
如果[mathjax]r\neq 0[/mathjax]，那么[mathjax]e^{rt}[/mathjax]就不是常数了，而是熟悉的指数曲线：
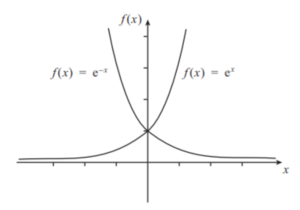
然后观察[mathjax]\left| C \right| e^{rt}\cos(\omega_0 t+\theta)[/mathjax]，理解为： 常数*一个指数级别变化的函数*一个永远落在[mathjax][0,1][/mathjax]范围内的三角函数 ，可以想像的到，最终的结果应该长这个样子：
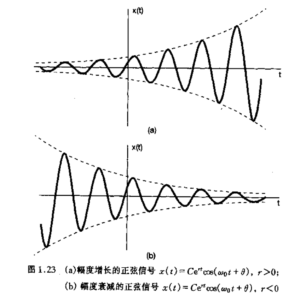
包络线来了！[mathjax]\left| C \right| e^{rt}[/mathjax]起着一种 振荡变化的包络作用 ，信号每次振荡的峰值正好落在2条包络线（分别由正弦函数的1和-1相乘得到）上，除峰值以外的信号部分则一定会落在2条包络线之间。
离散信号的几种表示方法
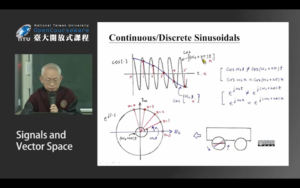
上面学的都是连续信号，现在学习离散信号的复指数信号与正弦信号
[mathjax-d]x[n]=Ce^{\beta n}[/mathjax-d]
学习欧拉公式了以后我们知道e的纯虚数次方可以和极坐标相互转换。所以上面这个信号公式还可以写为：
[mathjax-d]x[n]=Ca^n[/mathjax-d]其中[mathjax]C[/mathjax]和[mathjax]a[/mathjax]一般都是复数（当然也可以为实数）。
实指数信号
[mathjax-d]x[n]=Ca^n[/mathjax-d]如果[mathjax]C[/mathjax]和[mathjax]a[/mathjax]都是实数，那没什么可讨论的：
example：
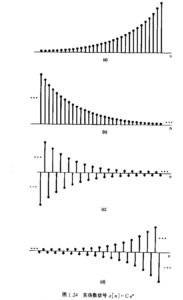
[mathjax-d]x[n]=Ce^{\beta n}[/mathjax-d]
如果[mathjax]\beta[/mathjax]是纯虚数，那么信号就变成了熟悉的正弦信号。
一般复指数信号（离散）
和连续复指数信号的核心内容基本上差不多。
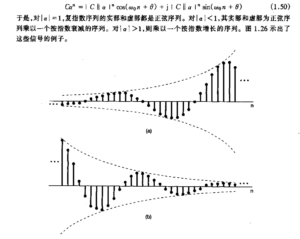
复指数周期信号：离散和连续的对比
信号的振荡程度
P19
连续信号 [mathjax]x(t)=e^{j\omega_0 t}[/mathjax] 有一个重要特性，就是：无论[mathjax]\omega_0[/mathjax]如何取值，它都是周期信号，且周期计算为：[mathjax]T=\frac{2\pi}{\left| \omega_0 \right|}[/mathjax].
所以可以想象，当[mathjax]\omega_0[/mathjax]单调递增时，信号的周期一定会单调递减，这个信号看起来就“振荡越剧烈“。
离散信号：[mathjax]x[n]=e^{j\omega_0 n}[/mathjax]却无法拥有这个性质。
所以说，对于写成[mathjax]e^{j\omega_0 n}[/mathjax]形式的离散信号而言，增加[mathjax]\omega_0[/mathjax]就像是在圆周上跑步，跑了一周（[mathjax]2\pi[/mathjax]）又跑回到了原来的位置（指信号本身没变）。
相关内容在2022-08-25的笔记里也有提到。preview
离散信号的周期判断
注意这个问题不要和上面的话题混淆。同样是变化[mathjax]\omega_0[/mathjax]的数值，前一个话题讨论的是 （修改[mathjax]\omega_0[/mathjax]前后）信号会不会发生改变 ，而这个话题讨论的是 信号是否为周期信号 .
同样我们要注意到基波周期的问题。比如我们在某次计算中进行到了这一步：[mathjax]x[n]=e^{j\omega_0 n}[/mathjax]，已知[mathjax]\omega_0=31\pi[/mathjax]，求这个离散信号的周期。很显然，我们有：
[mathjax-d]\displaylines{\omega_0 \cdot N= 2\pi \cdot m \cr 31\pi \cdot 2=2\pi \cdot 31 \cr}[/mathjax-d]先等一等！我们求出来的N=2仅仅是 基波周期 ，事实上我们当然能得到一系列周期N=2, 4, 8, ...：
[mathjax-d]\displaylines{\omega_0 \cdot N= 2\pi \cdot m \cr 31\pi \cdot 2=2\pi \cdot 31 \cr 31\pi \cdot 4=2\pi \cdot 62 \cr 31\pi \cdot 6 = 2\pi \cdot 93 \cr ...}[/mathjax-d]小结
下面这张表是从新书上面截的，更清晰一些：
例题
例题：
求这个离散信号的基波周期：
[mathjax-d]e^{j(\frac{2\pi}{3})n}+e^{j(\frac{3\pi}{4})n}[/mathjax-d]题目和答案在新书P19（是新书！）
后续：这道题的答案提醒了一个很重要的内容：
回顾一下傅里叶级数：
[mathjax-d]x(t)=\sum_{k=-\infty}^{+\infty}a_k e^{jk\omega_0 t}[/mathjax-d]由于k=0, 1, -1, 2, -2 ... ，可以想象得到，除去k=0, 1, -1的特殊情况，其他所有傅里叶级数[mathjax]e^{jk\omega_0 t}[/mathjax]（去掉分量[mathjax]a_k[/mathjax]），都是比[mathjax]\omega_0[/mathjax]的频率要更高的，换成周期来看就是：周期会越来越小，信号谱线的振动频率越来越快。
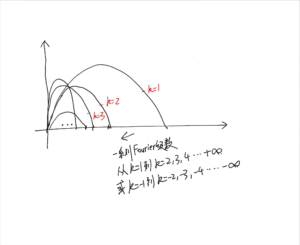
看起来就像是k=1的傅里叶级数把剩下的k=2, 3, 4, ... “包”在基波周期T/N里面了。那么问题来了，这些傅里叶级数组合成的信号[mathjax]x(t)\ \text{or}\ x[n][/mathjax]，基波周期是否为T或N呢？在这个问题上，离散和连续信号的答案是一样的吗？
当然是的，但为什么会有这么愚蠢的问题呢？大概是因为求解连续、离散信号的周期时，对最大公倍数的计算过程时相似的，这一点迷惑了我的想法。
以后如果复习到这里，可以先做一道小例题：求下面这两个信号的周期，并比较计算过程中相似和不同的部分。
[mathjax-d]x(t)=e^{j(\frac{2}{3})t}+e^{j(\frac{3}{4})t}[/mathjax-d]以及
[mathjax-d]x[n]=e^{j(\frac{2}{3})n}+e^{j(\frac{3}{4})n}[/mathjax-d]当然我们可以一眼看出[mathjax]x[n][/mathjax]因为角频率不含[mathjax]\pi[/mathjax]，铁定不是周期信号。下面从头开始计算并比较不同：
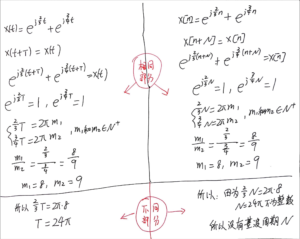
P.S. 如果要继续复习傅里叶级数，可以继续上面的题目进行推导。
但是又要注意一点：当看到下面这2组信号的时候，要意识到它们在某些方面有所不同：
[mathjax-d]x(t)=e^{j(\frac{2}{3})t}+e^{j(\frac{3}{4})t}[/mathjax-d]和
[mathjax-d]x(t)=e^{j\frac{\pi}{4}t}+e^{j\frac{2\pi}{4}t}+e^{j\frac{3\pi}{4}t}[/mathjax-d]不同在哪里？我可以一眼看出第2个信号的周期，但第1个信号的周期是需要用最大公倍数去计算的！
因为可以一眼看出第2个信号写成了标准的傅里叶级数的形式，所以我们直接观察[mathjax]e^{j\frac{\pi}{4}t}[/mathjax]就可以得到[mathjax]x(t)[/mathjax]的周期为[mathjax]\frac{2\pi}{\omega_0=\frac{\pi}{4}}=8[/mathjax] .
再观察这个信号：
[mathjax-d]x(t)=e^{j\frac{1\pi}{2}t}+e^{j\frac{3\pi}{4}t}[/mathjax-d]这个信号虽然也写成了傅里叶级数的样子，但它的周期还是难以一眼就确定，因为[mathjax]\omega_0[/mathjax]被隐藏了。
所以最后的结论是：
要牢牢记住周期信号展开傅里叶级数的样子：以信号的周期为最长周期，作为傅里叶级数中的[mathjax]k=\pm 1[/mathjax]项，剩余的傅里叶级数一律“压缩”在这个最长周期之内。就像这样。
但这个“最长周期”也是不容易求的，大多数时候都无法一眼看出来，除非这个信号写成了傅里叶级数的样子并直接写明了[mathjax]\omega_0[/mathjax]的数值。example 和 反例
后续内容
接下来处理P23的这部分内容：
推导：
学到冲激了！今天的笔记就写到这里。
