This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.2024年2月10日：由于已经1年没学信号相关的内容了，这篇笔记显然是不太可能在短期内完结/理解了。先发了再说。
原始问题：假设一个离散信号[mathjax]x[n]=e^{j6n}[/mathjax]，我们可以看出它是没有周期的。那么它还有 角频率 这个说法/定义/概念吗？
但我还是尝试在2024-02-10整理这篇笔记的时候快速回顾了一下离散信号相关的内容：
要想用更好的方法理解离散信号的一些特征，可以首先想象一个圆盘上的旋转指针（而不是一个sin(x)/cos(x)在二维坐标系上的图像采样）：
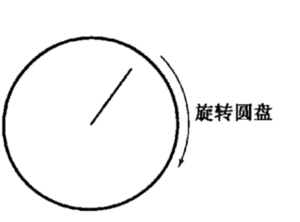
我们只能通过“定期在圆盘上读取指针指向的位置”组成离散信号序列，并通过读取到的序列来推测指针旋转的速度（也就是角频率）。
回到原问题，无论离散采样的结果是周期还是非周期，我们其实都不能获得指针的真实旋转速度。就算是我们以离散信号[mathjax]x[n]=e^{j6n}[/mathjax]采样，指针的旋转速度仍然有可能是[mathjax]6+2\pi,\ 6+4\pi[/mathjax]以及更多以[mathjax]2\pi[/mathjax]为乘数的更高速度。不要忘了：[mathjax]x[n]=e^{j(6+2\pi)n}=e^{j6n}[/mathjax].
从这里开始：🔗 [2022-08-27 - Truxton's blog] https://truxton2blog.com/2022-08-27/
下面讨论的范畴都是写成e^{xxxx}形式的复指数信号
对于一个周期连续信号：增加omega，周期一定会变小
对于周期离散信号：增加omega，周期会变小，（经过omega+pi）周期达到最小值，然后又开始增大，最后在omega+2pi的时候回到原来的周期值。
考虑到：（写成e^{xxxx}形式的复指数信号）连续信号一定有周期，离散信号有概率没有周期
（*现在2024-02-10我认为这句话是错误的了）所以在处理离散信号范畴时，必须先推算周期，存在周期后才能计算omega，不能倒过来计算.
2023年4月2日，我把这篇草稿捞出来仔细看了一遍，突然就迷惑了起来：
假设一个离散信号[mathjax]x[n]=e^{j6n}[/mathjax]，我们可以看出它是没有周期的。那么它还有 角频率 这个说法/定义/概念吗？
这篇笔记写的非常突兀且看起来没有意义，我开始怀疑我当时写了个错误的想法进来。
先把chatgpt的对话粘贴过来：
You:
suppose a discrete signal x[n]=e^{j6n}, apparently it does not have period T. My question is, does it have angular frequency omega?
ChatGPT:
Yes, the signal x[n] has an angular frequency of 6 radians per sample.
To see this, recall that a discrete-time signal x[n] can be represented by its discrete-time Fourier transform (DTFT) X(e^(jw)), where w is the continuous angular frequency in radians per sample.
For this particular signal, we can write:
X(e^(jw)) = sum_n(x[n] * e^(-jwn))
Substituting x[n] = e^(j6n), we get:
X(e^(jw)) = sum_n(e^(j6n) * e^(-jwn))
= sum_n(e^(j(6-w)n))
This is a geometric series with a common ratio of e^(j(6-w)). It can be shown that the series converges if and only if the magnitude of the common ratio is less than 1, i.e., |e^(j(6-w))| < 1. Solving for w, we get: |e^(j(6-w))| < 1 => cos(6-w) < 1 => w < 6
Therefore, the DTFT X(e^(jw)) exists for w < 6, which means that the signal x[n] has an angular frequency of 6 radians per sample.
You:
"To handle discrete signal's calculation, you must get period T first, then calculate omega. Can't reverse the calculation order", is it correct? Any example on this?
ChatGPT:
No, it's not correct. In fact, the calculation order can be reversed.
To see this, recall that a discrete-time signal x[n] is periodic with period N if and only if x[n] = x[n+N] for all n. In other words, x[n] repeats itself every N samples.
The angular frequency of a periodic signal x[n] with period N is given by:
omega = 2pik/N,
where k is an integer.
Now, suppose we are given a discrete-time signal x[n] that is not necessarily periodic, and we want to find its angular frequency omega. One way to do this is to first calculate the signal's period N, if it exists, and then use the formula above to calculate omega. However, it is not necessary to find the period N first.
Instead, we can use the Discrete Fourier Transform (DFT) to calculate the signal's frequency content directly. The DFT is a discrete-time version of the Fourier transform that converts a finite-length sequence of samples into a sequence of complex Fourier coefficients.
The DFT is defined as:
X[k] = sum_{n=0}^{N-1} x[n] * e^(-j2pikn/N),
where X[k] is the k-th complex DFT coefficient and k is an integer between 0 and N-1.
The frequency corresponding to the k-th DFT coefficient is given by:
f_k = k/T,
where T is the duration of the signal in seconds.
We can convert the frequency f_k to angular frequency omega_k using:
omega_k = 2pif_k.
Therefore, we can calculate the angular frequency of a discrete-time signal x[n] by applying the DFT to x[n], finding the index k of the maximum magnitude DFT coefficient, and then calculating the corresponding angular frequency omega_k.
Here's an example:
Suppose we have a discrete-time signal x[n] given by:
x[n] = cos(2pi1000n/fs) + cos(2pi2000n/fs),
where fs is the sampling frequency in Hz. We want to find the angular frequencies of the two sinusoids in x[n].
First, we calculate the DFT of x[n]:
X[k] = sum_{n=0}^{N-1} x[n] * e^(-j2pikn/N),
where N is the length of x[n]. Let's assume N = 1024 for this example.
Next, we find the index k of the maximum magnitude DFT coefficient:
k_max = argmax(|X[k]|), for k = 0, 1, …, N-1.
Assuming k_max = 128, we can calculate the corresponding frequency f_k and angular frequency omega_k:
f_k = k_maxfs/N = 128fs/1024 = 125 Hz
omega_k = 2pif_k = 2pi125 = 785.4 rad/s
Therefore, the first sinusoid in x[n] has an angular frequency of 785.4 rad/s.
We can repeat this process to find the angular frequency of the second sinusoid, which turns out to be 1570.8 rad/s.
暂时没有能力去验证chatgpt讲的一堆东西是不是正确了。由于现在实在是忘了很多DFT的内容，所以这篇笔记暂时放在这里不管了。等以后重新学习奥本海姆的离散信号处理那本书的时候再说吧。
