WARNING: This article may be obsoleteThis post was published in 2022-08-31. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今天从哪里开始？
昨天主要学习了傅里叶级数的推导。
继续昨天的笔记，从P119开始：
（继续2022-08-29的内容）推导：连续时间周期信号的傅里叶级数
笔记1
P119应该是非常难学的，不知道要花多久看完：
总的来说“从上往下推导”并不难，但第一步就非常诡异：我怎么知道第一步应该乘上这个奇怪的东西？
目前仍然 无法用非常自然的说法来进行这一步 ，当然，这一步的作用也是非常明确的，那就是为了得到这个公式：
[mathjax-d]\int_0^T \mathrm{e}^{\mathrm{j}(k-n) \omega_0 t} \mathrm{~d} t= \begin{cases}T, & k=n \\ 0, & k \neq n\end{cases}[/mathjax-d]
倒数第二行[mathjax]Ta_n[/mathjax]的一步推论也比较突兀和诡异，还是做点笔记吧：
笔记2：内积、共轭、正交
为了彻底理解这部分内容，决定先学点别的：
内积、共轭、正交
inner-product/dot-product, conjugate, orthogonal
看过的资料：（帮助比较大的用✅标记一下）
✅ 🔗 [Lect2witheqs] http://web.mit.edu/16.unified/www/archives 2007-2008/signals/Lect2witheqs.pdf
🔗 [复向量的内积,想不明白? - 知乎] https://www.zhihu.com/question/38227483
🔗 [如何理解复向量的内积？ - 知乎] https://www.zhihu.com/question/372106111
🔗 [共轭复数 - 维基百科，自由的百科全书] https://zh.wikipedia.org/zh-hans/共轭复数
🔗 [数字信号处理 - -内积与内积空间] http://www.qinglin-tang-scu.com/Lectures/FourierAnaLysis/Lec1.pdf
🔗 [Lp空間 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/Lp空间
✅ ✅ 🔗 [深入理解傅里叶变换（番外）.傅里叶级数的意义 - 知乎] https://zhuanlan.zhihu.com/p/52977221
🔗 [基 (線性代數) - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/基_(線性代數)
🔗 [Hermitian Inner Product -- from Wolfram MathWorld] https://mathworld.wolfram.com/HermitianInnerProduct.html
然后放一些笔记：
特别注意：下面的笔记很大程度参考了🔗 [深入理解傅里叶变换（番外）.傅里叶级数的意义 - 知乎] https://zhuanlan.zhihu.com/p/52977221，该笔记的图片备份：preview
其中这个笔记里最重要的一部分截图：
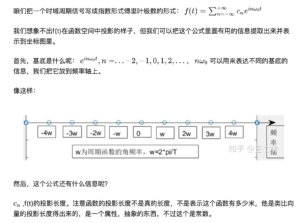
2022-09-02补充了一些类似于“勘误”的东西：
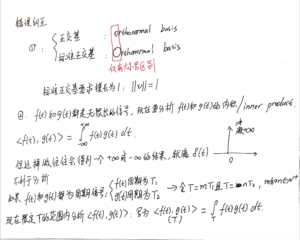
此外，在2022-09-02的笔记里，还用 切钢管 的例子来说明为什么可以取基波周期的范围进行分析：
下面是笔记：（注意：笔记中部分有关 正交基 的用词可能不准确，具体见本笔记前面的勘误）
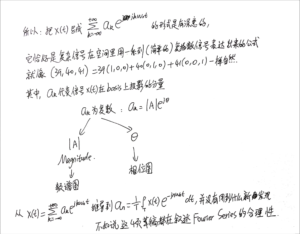
重要结论
所以这一步总算知道在做什么了：
笔记3：一些对空间映射的思考
一点思考：
从时域到频域，或许并没有某一个步骤是“神奇”的操作。所谓频谱图，本质上也就是把各个频率分量拉出来重新绘制一张坐标参考系不一样的图而已。比如x(t)=cos(t)，这个信号从时域转换到频域应该非常简单吧？复杂信号转换到频域也是一样，只是它需要用分解为一系列复指数信号而已...一旦推导到傅里叶级数，距离“频域”也就只有一步之遥了。所以说傅里叶级数的最核心一步就是在信号的希尔伯特空间里创造一组正交基...
* 有关希尔伯特空间的补充写在本文后面。
再补充一些内容：
一个复杂的信号就像...一个萨尔纳加神庙（乌尔纳），这个神庙位于无数平行宇宙之间的裂隙当中。每当一个平行宇宙（正交基）生成之时，萨尔纳加人就会使用化身降临到这个宇宙（投影能量为[mathjax]a_k[/mathjax]），开始创造新的生命。对每个特定的宇宙而言，只有特定的能量才能诞生新的生命（[mathjax]k=n[/mathjax]时的情形）；其他的能量仅仅是宇宙中无序的熵而已，这些熵无法构成任何生命体（正弦信号一个周期内的积分为0）。
一些例题
下面是一些例题。例题本身比较容易。
P120~P121
一个难一点的例题：
P121
不算难，但是等等，第一遍做的时候犯了一个严重的错误：对复指数信号的积分求错了：
（下面写的是正确的公式）
[mathjax-d]\int_{a}^{b} e^{j\omega_0 t}dt=\left . \frac{1}{{\color{red}j} \omega_0}e^{j\omega_0 t} \right|_a ^b[/mathjax-d]注意上面公式里红色的[mathjax]\color{red}j[/mathjax]，这个千万不能漏！
答案：P122
另外，这道题的答案似乎还和 包络线 有关。 上一次接触到包络线的笔记：🔗 [2022-08-27 - Truxton's blog] https://truxton2blog.com/2022-08-27/
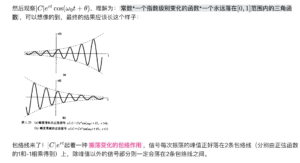
一些零散的结尾内容
继续：
似乎是讨论傅里叶级数的一些使用限制。准备先跳过再说。
学到这里：
到9月1号了！接下来的内容写到09-01的笔记中去。
补充：傅里叶级数所在的空间是否为希尔伯特空间？
在本篇笔记中有：
好像是的！🔗 [What are the uses of inner products in signal processing? - Quora] https://www.quora.com/What-are-the-uses-of-inner-products-in-signal-processing
更新：
到了2023年，chatgpt也回答了我相似的答案：
Chatgpt：是的，傅里叶级数所在的空间通常被称为[mathjax]L^2[/mathjax]空间，它是一个希尔伯特空间。[mathjax]L^2[/mathjax]空间中的元素是可积的函数，平方可积意味着函数的平方的积分在整个定义域内是有限的。在[mathjax]L^2[/mathjax]空间中，可以定义内积和范数，满足所有希尔伯特空间的基本性质，例如完备性和拓扑结构。傅里叶级数是[mathjax]L^2[/mathjax]空间的一组基，因此[mathjax]L^2[/mathjax]空间也被称为傅里叶空间。
