WARNING: This article may be obsoleteThis post was published in 2022-08-05. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今日总结
对本笔记的总结：
本篇笔记主要跟随Bilibili: 徐亦达机器学习 学习了Kalman Filter的入门知识，但并没有把6P视频完全看完看懂，因为涉及到了不会推导的矩阵运算内容。
在笔记的最后部分试图总结Bayesian Filtering与Kalman Filter的不同。
设置expose_php=ON会影响FastCGI的缓存文件大小
新发现：
如果php.ini设置了expose_php=ON，那么fastcgi缓存文件夹的体积会明显大一圈。这是因为开启expose_php时，每一个fastcgi缓存文件都会带上类似X-Powered-By: PHP/8.0.22 这样的标识头，而关闭expose_php就不会有这样的字段。
今日学习资料
最主要的资料：🔗 [徐亦达机器学习：Kalman Filter 卡尔曼滤波【2015年版-全集】_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1TW411N7Hg
所有接触过的资料：
🔗 [2022-08-02 - Truxton's blog] https://truxton2blog.com/2022-08-02/
🔗 [徐亦达机器学习：Kalman Filter 卡尔曼滤波【2015年版-全集】_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1TW411N7Hg
🔗 [2_28_2018.pdf] https://www.colorado.edu/amath/sites/default/files/attached-files/2_28_2018.pdf
🔗 [MI37slides-Kalman.pdf] http://www.sci.utah.edu/~gerig/CS6320-S2013/Materials/MI37slides-Kalman.pdf
有关Covariance：🔗 [2021-09-21 - Truxton's blog] https://truxton2blog.com/2021-09-21/ , 🔗 [2021-11-18 - Truxton's blog] https://truxton2blog.com/2021-11-18/#协方差_协方差矩阵
Stochastic differential equation—SDE
🔗 [Stochastic differential equation - Wikipedia] https://en.wikipedia.org/wiki/Stochastic_differential_equation
目前只需要记住它的简称为 SDE 即可。
Kalman Filter—B站徐亦达机器学习
今天从哪里开始？当然是kalman filter！这是上一篇笔记（2022-08-02）没有搞完的内容。
学习：
🔗 [徐亦达机器学习：Kalman Filter 卡尔曼滤波【2015年版-全集】_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1TW411N7Hg
入门部分
注意到p1 6:00左右提到了HMM观测值之间没有关联：
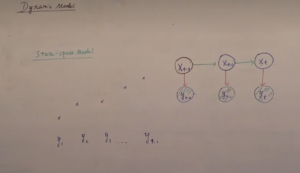
这部分内容可以回顾https://truxton2blog.com/wp-content/uploads/2022/08/20220804_164856_U0tDK.png：
p2 11:15左右
看到这里就找到了bayesian filtering到kalman filter的一个重要区别：
目前学过的HMM模型，状态都是离散值，所以转移概率是从「一步Markov转移矩阵」里面查表得到的。
如果状态是连续的怎么办？所以这就是kalman filter里面的内容了！
一个比较难以理解的内容
理解这部分内容花了比较长的时间：
主要原因是没有正确理解这部分内容的符号[mathjax]\mathcal{N}[/mathjax]是怎么去掉的：
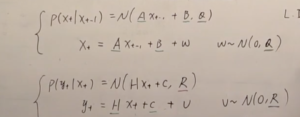
想了很久，大概是明白了，纯粹就是Probability Density Function相关的内容忘记了，记忆不够生动，导致很多东西想象不出来。
矩阵A到底是什么？
[mathjax-d]X_t=AX_{t-1}+B+\omega[/mathjax-d]这里的[mathjax]A[/mathjax]到底是什么？是一个常数，还是...？大多数教材都会称它为 state transition matrix ，那是不是和HMM的...状态转移矩阵...差不多？
当然不是一个东西！这里如果写成：[mathjax]X_t=f(X_{t-1})+B+\omega[/mathjax]就会更容易理解了。
在后续笔记中也有提到：🔗 [2022-08-10 - Truxton's blog] https://truxton2blog.com/2022-08-10/#（几乎没有学进去）继续在kalmanfilternet上面学习kalman_filter
用通俗的语言描述Kalman Filter的状态转移流程
现在继续看视频：
目前学习的「kalman状态转移」大概就是：
在一个markov chain上，状态是连续的；
从时间t-1的状态转移到时间t时，首先会指定一个“无偏转移”（自创用语，表示Ax+B），然后状态会在“无偏转移”的基础上发生一定的偏差（偏差遵循高斯分布）；
状态确定好以后，使用类似的规律（产生观测值，但有高斯噪声偏移）产生观测结果；
然后继续下一个状态。从什么地方继续？从时间t的状态继续（上面那张图右下角的黑点），而不是从时间t的观测继续。
最后：类似[mathjax]\mathcal{N}(Ax+B, Q)[/mathjax]这样的计算方式，在视频里称为“线性高斯”。
例题：小车匀加速
物理：复习速度和加速度（最简单的线性加速）
接下来开始推导视频part 4（https://www.bilibili.com/video/BV1TW411N7Hg?p=4）
要点1：虽然加速度服从正态分布，但在单位时间delta t之内它是一个常数，是保持不变的！所以我们可以用简单的物理知识（均匀加速运动）来表示一些公式。
前面的笔记都能推导，但最后一步得出结论（P3 11:25左右）的时候遇到了一些理解问题：
原来我需要补习这个：🔗 [statistics - What is the expectation of $ X^2$ where $ X$ is distributed normally? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/99025/what-is-the-expectation-of-x2-where-x-is-distributed-normally
[mathjax-d]E\left(X^{2}\right)=\operatorname{Var}(X)+[E(X)]^{2}[/mathjax-d]在P6 2:00左右补充了一个东西很有用（红色方框所示的内容）：
* 下面这张图省略了[mathjax]B[/mathjax]，因为[mathjax]B[/mathjax]对结论没有什么影响（原视频里有解释）
推导笔记：
遗留的未解决问题（这个例题最后得出了什么有用的结论？）
现在已经把视频里的所有推导都复现了一遍，唯一的问题在于：视频里似乎没有做出所谓的「最终结论」，我现在知道A和B如何表达，但不知道噪声如何表达，以及协方差矩阵的最终作用到底是什么。
打算继续看视频，听懂了再返回来把笔记整理一遍。
继续学习了一点点内容
补充知识：
p6 16:17左右
如果[mathjax]X[/mathjax]的 均值/期望 为0，那么[mathjax]\mathcal{cov}(X)=\mathop{\mathbb{E}}(XX^T)[/mathjax] .
深夜回顾：Kalman Filter和Bayesian Filtering到底有什么区别？
2022-08-06：
停！看来kalman filter今天是没法100%搞明白了。决定先把「小车加速」的例题推导整理出来，然后回顾今天学习的所有内容。
回顾什么内容呢？
还是从贝叶斯滤波开始回顾：
贝叶斯滤波，状态为离散值，转移概率要查表（转移矩阵），发射概率可以是古典概型也可以是gaussian mixture model也可以是其他。
kalman filter，状态为连续值；转移到下一时刻时：先做线性变换Ax+B，然后基于Ax+B为期望值偏移一定范围（正态分布）；发射概率是正态分布。总之现在一切都是正态分布：状态的概率分布，转移方法，发射概率。
预测（prior）也是正态分布，后验（posterior）也是正态分布。
看看现有认知是否和wikipedia一致：
找出上一篇笔记：🔗 [2022-08-02 - Truxton's blog] https://truxton2blog.com/2022-08-02/#试图过渡到Kalman，但没有完成
今天必须搞清楚这部分内容才能结束！
当前持有的结论： （限定：discrete time） 最普通的那个kalman filter就是状态空间连续的Bayesian filtering.
The Kalman filter is then an algorithm for sequentially updating the distributions of [mathjax]\mathbb{X}_{k}[/mathjax] given observed [mathjax]\mathbb{y}_{1}, \ldots, \mathbb{y}_{k}[/mathjax] in this dynamic Bayesian network. The only probability theory required is computing conditional distributions of (finite-dimensional) multivariate Gaussian distributions.
https://stats.stackexchange.com/questions/232594/why-is-the-kalman-filter-a-specific-case-of-a-dynamic-bayesian-network
看看这个链接有没有用：
🔗 [machine learning - Difference between Hidden Markov models and Particle Filter (and Kalman Filter) - Cross Validated] https://stats.stackexchange.com/questions/183118/difference-between-hidden-markov-models-and-particle-filter-and-kalman-filter
再看一个：🔗 [machine learning - Why is the Kalman Filter a specific case of a (dynamic) Bayesian network? - Cross Validated] https://stats.stackexchange.com/questions/232594/why-is-the-kalman-filter-a-specific-case-of-a-dynamic-bayesian-network
所以，最后回到那个万恶的wikipedia：
目前认为那个 However 所指的是「However，kalman处理的是连续状态空间」。
最后，有关kalman filter的probability graphical model
总之就是，现在学习的只是最基本的probability graphical model，放心去用那些熟悉的概率模型就可以了！
