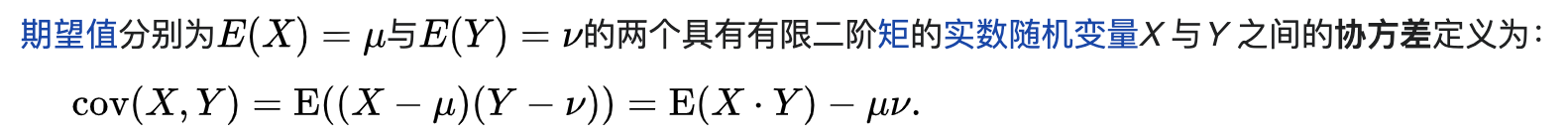WARNING: This article may be obsoleteThis post was published in 2021-09-21. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.主要内容：多元正态分布/多元高斯分布 / multivariate gaussian distribution / multivariate normal distribution / MVN
连续型随机变量的密度函数
https://www.zhihu.com/question/36853661
搜索关键词[pdf of continuous random variable]
https://www.math.arizona.edu/~jwatkins/f-transform.pdf
附加：递增函数的反函数也是递增的
所以如果要满足上图公式，一定要保证g(x)递增
查找关键词：[cumulative distribution of continuous random variable]
中心极限定理
协方差
* 后续笔记：🔗 [2021-11-18 - Truxton's blog] https://truxton2blog.com/2021-11-18/#协方差_协方差矩阵
https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE
协方差矩阵
🔗 [2022-08-07 - Truxton's blog] https://truxton2blog.com/2022-08-07/#协方差、协方差矩阵的计算（附带例题）
* 后续笔记：🔗 [2021-11-18 - Truxton's blog] https://truxton2blog.com/2021-11-18/#协方差_协方差矩阵
https://zh.wikipedia.org/zh-hans/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5
https://zhuanlan.zhihu.com/p/349802953
二维协方差矩阵的旋转角度表达方式（covariance matrix ellipse axis）
https://blog.csdn.net/htuhxf/article/details/107738233 , https://zhuanlan.zhihu.com/p/37609917
P-value / [mathjax]p(x)[/mathjax] :https://www.zhihu.com/question/23149768/answer/282842210
多元正态分布/多元高斯分布/ MVN
一个非常直观、在开始数学公式推导之前的入门视频：https://www.youtube.com/watch?v=azrTdjrA2bU
首先是MVN的简单介绍：https://www.zhihu.com/question/36339816/answer/385944057
wikipedia: https://en.wikipedia.org/wiki/Multivariate_normal_distribution
Derivative of multivariate normal distribution
https://stats.stackexchange.com/questions/27436/how-to-take-derivative-of-multivariate-normal-density
但是首先需要理解矩阵的导数运算问题，见：https://zhuanlan.zhihu.com/p/263777564
OCR辅助查找工具
The easiest case for transformations of continuous random variables is the case of g one-to-one. We first consider the case of g increasing on the range of the random variable X. In this case, g 0-1 is also an increasing function. To compute the cumulative distribution of Y = g(X) in terms of the cumulative distribution of X, note that Fy (y) = P{Y ≤ y} = P{9(X) ≤ y} = P{X ≤ g-1(y)} = Fx(9-1(y)).期望值分别为E(x）二1与E(Y）=V的两个具有有限二阶矩的实数随机变量X与丫之间的协方差定义为： cov(x,Y=E((×-④(Y-D)=E(X.Y-w.
