This post was published in 2023-08-28. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
(Top)
使用的是第4版(2009)
chapter 2 solving linear equations
chapter 1的笔记:🔗 [introduction to linear algebra - chapter 1学习 - Truxton's blog] https://truxton2blog.com/introduction-to-linear-algebra-chapter-1/
2.1 vectors and linear equations
2.1 vectors and linear equations
行空间/列空间
row picture and column picture
行空间/列空间
p34
看到这里才确认这本书确实是和MIT 18.06联系在一起的,这本书的chapter 1可能是被跳过了,视频的第一节就是从row picture/column picture开始讲的

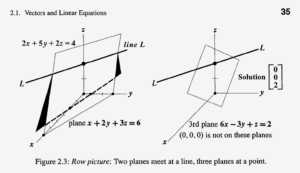
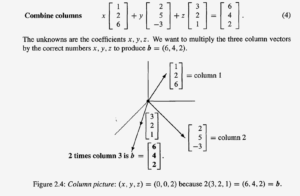
可以从row picture和column picture两个角度再次想象一下矩阵满秩/不满秩的情形:
row picture,不满秩:张成的空间维度不够
column picture,不满秩:由于这些向量并不是线性无关的,至少有1组向量(记为k)可以用其他向量线性表达,这就意味着column k处在那个线性表达的空间里面,无法形成更高的维度。
此外p47还能看到2维坐标系下的不满秩情况:
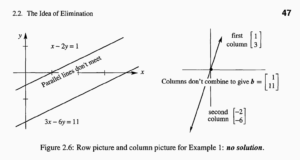
上一张图居然提到了无解的情形,这个时候回忆上一个笔记就会发现no solution的情况似乎并没有列出来。这其实并不矛盾,因为上一个笔记的情形是Ax=0,在Ax=0(homogeneous system,齐次坐标系)的范畴内只有两种情况:唯一解,和无穷多的解。而在Ax=b(b≠0,非齐次坐标系)的范畴内有3种情况:唯一解,无穷多的解,没有解。这部分内容可以参考🔗 [rank2005.pdf] https://www.math.tamu.edu/~fnarc/psfiles/rank2005.pdf
或者说,Ax=0再不济也有x=0这个一定存在的解
| one solution | infinite solutions | no solution | |
| Ax=0 | ✅ | ✅ | ❌ |
| Ax=b (b≠0) | ✅ | ✅ | ✅ |
此外p48还能看到2维坐标系下的无穷解-不满秩的情况:
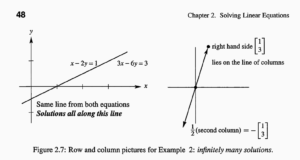
以及再一次记住Ax=b的两种表达方式

做点题目
好像都学过了,看看题目
29和30
马尔可夫矩阵
当然以前写过这样的程序:🔗 [2021-12-21 - Truxton's blog] https://truxton2blog.com/2021-12-21/
直接把程序搬过来就能用:
import numpy as np
def pn(a, n):
k = a
for i in range(0, n):
k = k @ a
return k
a = np.array([
[0.8, 0.7],
[0.2, 0.3]
])
print(pn(a, 5))
print()
print(pn(a, 10))
print()
print(pn(a, 20))
print()
print(pn(a, 100))
print()
print(pn(a, 200))
当然,另一边也要试着推导一下马尔可夫矩阵的这一性质:

注意,上面的这张草稿仅仅是推导了“如果markov matrix的迭代运算最终确实会收敛于某个向量,那么这个向量可能是xxxxx“,没有证明”markov matrix的迭代计算一定会收敛于向量xxxxxxx“,具体的证明暂时不管了,因为似乎涉及到后面的特征向量和特征值
先不管31的后续了,再看32
魔术方阵/magic matrix,仅仅是31题并不难,但这个概念以后可能还要深入了解
32 很容易
33 完全不会,看答案去了
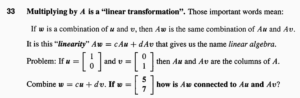
可能是想得太绕了,或者总是想着推导出什么更直观的结论,实际的答案并没有那么复杂:
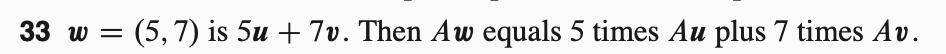
34 很容易,不知道为什么放在challenge problems
35 先不管了
2.2 the idea of elimination
2.2 the idea of elimination
复习一下pivot
P46

The pivots are on the diagonal o f the triangle after elimination.(p46)
比如
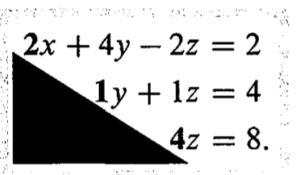
从第一行开始,piviot:2, 1, 4
p45
elimination的效果
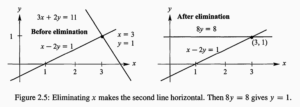
然后就是elimination的规范:虽然我们手算简单消元的时候可能因为图省事而优先消去那些“看起来好消的”,但实际上elimination仍然有规范的:p49:

forward和backward
就是从字面意思理解
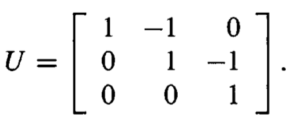
L(lower triangular)使用forward,从顶部向下逐一求解
breakdown就是无法通过消元形成upper/lower triangular的情形
row exchange也是一个规范操作,对付Temporary Failure,尽管我们用各种不规范的方法解简单的二元/三元方程的时候很可能直接就忽略了:
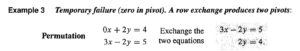
做点题目
做题
problem set 2.2
p53 #11

尤其是(b),可以多想一想为什么
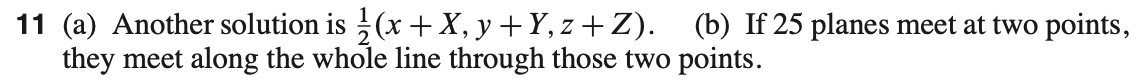
p54 #25
随便挑了一题就做错了:

需要注意这道题(或者说这类题)一般都不止一个答案:
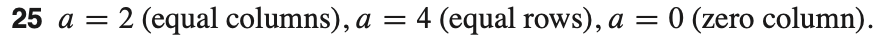
看看challenge problems
p55 #30

答案:
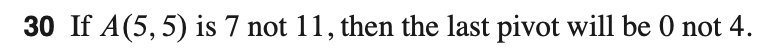
p55 #31
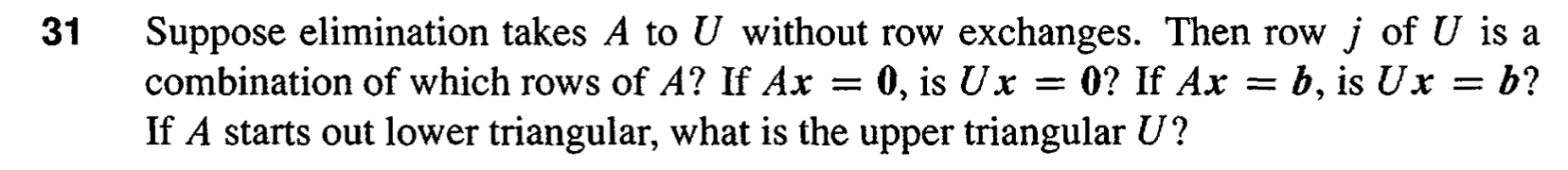
几个结论(或者说和直觉相关的东西)都挺有用的。
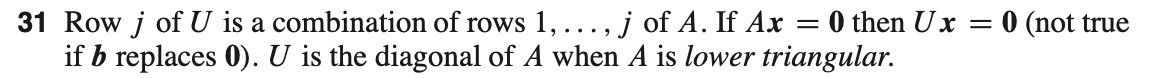
p55 #32

重点看(或者说是想象)问题(d)
答案:

隔了差不多一个星期没进度学了,继续:
(没有继续了,这个系列草草结束)