This post was published in 2023-06-22. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
2024年写的总结
2024年8月:臃肿的笔记,学习范畴大概是从“不知道线性规划是什么“到”勉强理解了simplex algorithm的作用和一些细节”。基于对去年LP学习情况的总结(LP学了但又没学精,也没有继续深入学习凸优化或者整数规划),这篇笔记大概是这么个情况:本篇笔记基本不涉及simplex实战(LP-Tableau),以数学推导为主,所以应该会有很多错误,不推荐作为【长时间没看LP需要重新捡起】的复习笔记,只能用来作为资料查找。
因为错过了纠正本篇笔记的最佳时机(2023年12月),现在(2024年8月)已经忘光了LP的大部分内容,所以本篇笔记的错误内容也不知道什么时候能纠正了,只能先把笔记发出来。
关于这篇笔记
这篇笔记有潜力成为巨无霸2022-03-20之后的又一篇长长长垃圾笔记。注意:相比于原本的草稿笔记,这篇(p = 12119)可能会增加/删除大量内容。
最简单的线性规划例题(高考)
先来点高考难度的线性规划题:
https://zhuanlan.zhihu.com/p/62918890
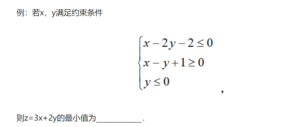
答案是-18
准备一些资料
本篇笔记主要参考的
写完整篇笔记以后补充的:
虽然要学习的书是《Introduction to Linear Optimization》,但实际学习起来并没有参考这本书
主要参考了以下资料:
🔗 [【运筹学】6小时不挂_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1pA411H76k/
主要是看p1~p4,知道有单纯形法这个东西,但没有去具体学习/记住 如何填那个单纯形法的表
最重要的内容是“化标准型”,在高维空间理解线性优化的本质

🔗 [Visualizing the Simplex Algorithm - Daniel Nichols] https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm

看完这篇博客的大部分内容,对“线性优化到底是在高维空间做什么”有了直观认知。
🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892
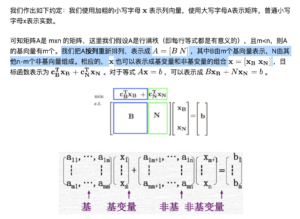
主要参考这篇博客的前50%的内容,从公式的角度理解单纯形法
可惜后面遇到了一些内容实在理解不了,所以转向了这篇博客背后的书《最优化理论与算法》,理解了单纯形法剩下的一些内容
《最优化理论与算法》

通过看p37~p40,终于理解了单纯形法的一些细节(为什么要这样做,为什么这样做可以保证xxx)
原始笔记
也就是刚开始写笔记的时候准备参考的资料:

🔗 [【运筹学】6小时不挂_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1pA411H76k
🔗 [运筹学(最优化理论)如何入门? - 知乎] https://www.zhihu.com/question/22686770
🔗 [【公开课】线性规划 方述诚_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1A5411r7TK/
bilibili猴博士-运筹学视频
介绍
先看这个:
🔗 [【运筹学】6小时不挂_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1pA411H76k
非常以考试解体为导向,所有内容的目标只有解题
一共12p,从p=1开始看
p1 线性规划建模
p1 线性规划建模
例题:
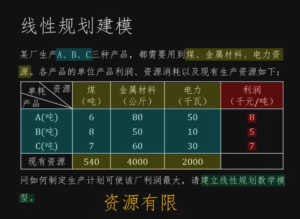
只是列举限制条件的话很简单,一般会先列出这样的:
注:这张图的公式是不完整的

因为还少写一个限制条件:
[mathjax-d]x_1,x_2,x_3\geq 0[/mathjax-d]
所以一开始的步骤应该这样写:

p3 图解法
p1看完了,继续
先看p3 图解法
由于p3的大部分内容都是高考难度的题,所以先记一下相关内容

答案:[mathjax](x_1,x_2)[/mathjax]为[mathjax](5,2)[/mathjax]时,[mathjax]max(x_1+x_2)=7[/mathjax] .
剩下的题也都差不多:

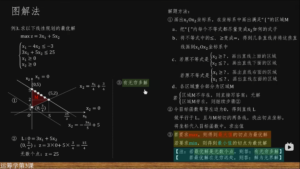
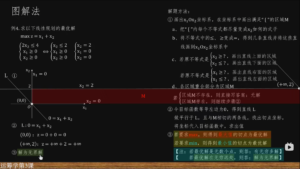
额外内容:
凸集和凹集:
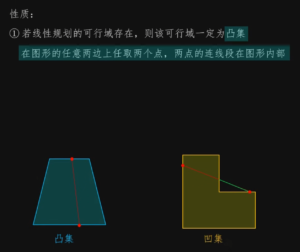
p2 化标准型
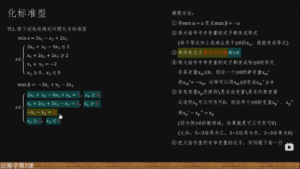
下面是p2:化标准型
仅仅是一个”化标准型“的过程,并不涉及”化标准型“以后的解法
没有什么数学难度,但过程比较多,“标准型”的要求也比较多
例题:

最终答案:

一些中间过程:





p4 单纯形法
继续p4 单纯形法
起始问题:

先根据p2的“化标准型”,把它改造一下:

答案在左下角:
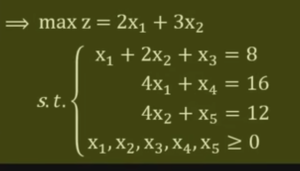
然后继续:

把上一张图的左下角的内容改写为:

至少到了这一步,上面这张图的内容看起来是非常有意义、积极向上的,
但后面的“单纯形表填写”就完全不一样了:
不仅要构造一张(结构复杂)的单纯形表,还要对这张表的内容进行很多步手算,其中还包括对表中很多字段的反复填写+擦除:
(下面的内容非常长,而且步骤复杂又复杂)

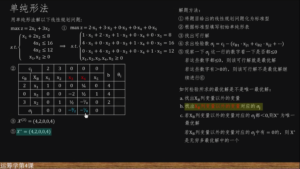
p4有48分钟,其中45分钟都在讲这张单纯形表怎么填写数字。
决定暂时跳过看看这个单纯形法是不是什么过时又老的手动计算考试题
也许单纯形法并不是什么很过时的方法,但我需要学到某个阶段,在这个阶段里,单纯形法的整个流程都可以直观的用计算机矩阵计算/程序代码 的方法求解。就像p4的前几分钟一样(把一般线性规划的题转换为标准型,再转化为单纯形法可以使用的格式)

(2023年9月补充)标准型和规范型(standard form/canonical form)
直接从linear programming and network flows第四版的P6抄过来

过渡内容:尝试系统学习一下单纯形法
注:看完猴博士的视频的p1~p4后还不知道单纯形法是一个计算高效的综合算法,以为只是一个填表游戏
(尝试)系统学习一下单纯形法
从暴力做题机转向一般化的公式学习
中途查了一点关于p4 单纯形法对应的资料:
单纯形法,simplex algorithm
似乎是大有学头
对应《Introduction to Linear Optimization》第3章:preview
(就看了个简单的开头)🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892

上面这张图对应了p4的前几分钟内容
然后继续找“直观、可视化理解”:
youtube搜索simplex algorithm visualization
🔗 [simplex algorithm visualization - YouTube] https://www.youtube.com/results?search_query=simplex+algorithm+visualization
视频:
🔗 [Simplex Explained - YouTube] https://www.youtube.com/watch?v=jh_kkR6m8H8&t=417s
手绘,但讲述了一个重要内容:
以二维坐标系的线性规划为例,假设现在画出了这样一个“约束区域”
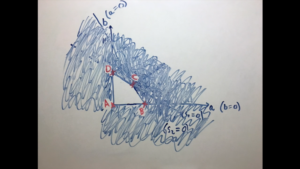
所以最优的点应该是在ABCD这4个点里面产生
高中数学方法:用斜率确定、常数不确定的直线去“试“
simplex algorithm:从A点出发,走AB到B,再走BC到C,(通过一些方法和限制)最后停留在C点不走了,所以C就是最优取值点
再看一个视频:
很短,没有讲解,只是动画 🔗 [Simplex Algorithm - YouTube] https://www.youtube.com/watch?v=54blxYi5JF8
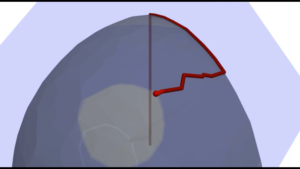
大概也是类似的“移动”的意思。
视频comment:
The Simplex Algorithm solves linear optimization problems by progressing from an initial vertex (the origin in this case) of the admissible domain along the edges always increasing the target value until it reaches the maximum. The path of the solution point is drawn in red. The admissible domain in this animation is formed by a set of tangent planes to the unit sphere equidistributed in the first octant. The target function is x+y+z, its level surface through the current tentative solution point is shown in light blue.
https://www.youtube.com/watch?v=54blxYi5JF8
再看一个视频:
🔗 [Simplex Algorithm - YouTube] https://www.youtube.com/watch?v=Ci1vBGn9yRc
simplex:
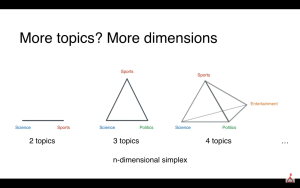

暂时没懂,等待后续处理
再换一个看
好像找不到类似3blue1brown那样的高维空间可视化simplex algorithm的视频了
再查查google
博客:Visualizing the Simplex Algorithm - Daniel Nichols
part1
看🔗 [Visualizing the Simplex Algorithm - Daniel Nichols] https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm
example:
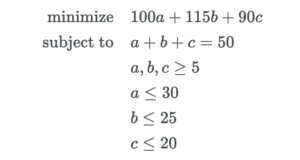
可以写为

上面这个应该就是“化标准型”的最终要求对应的抽象的矩阵公式
补充:先前学习的“化标准型”的这一步添加的新的参数的步骤被称为“添加松弛变量” / add slack variables
对解空间的理解
继续看:“解空间” - solution space
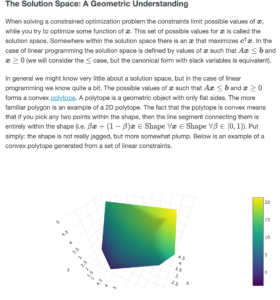
This set of possible values for [mathjax]\boldsymbol{x}[/mathjax] is called the solution space.
simplex algorithm对应的解空间一定是convex polytope.
多胞形 / Polytope / 多面体
🔗 [Polytope - Wikipedia] https://en.wikipedia.org/wiki/Polytope
A polytope is a geometric object with only flat sides.
https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm
反例:non-polytope,比如球体、圆柱体、圆锥体
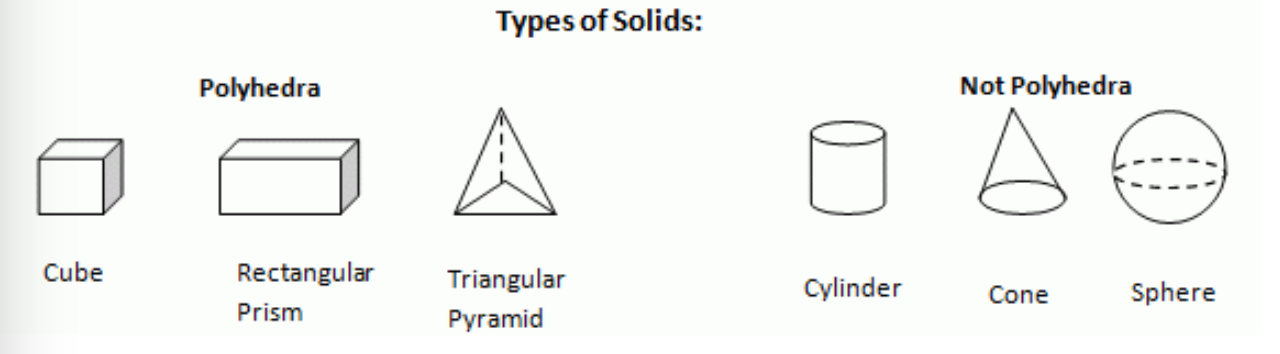
(继续)...而convex polytope就意味着
The fact that the polytope is convex means that if you pick any two points within the shape, then the line segment connecting them is entirely within the shape
https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm
继续
[mathjax]n[/mathjax]-dimensional hyperplane
在2D平面上这就是一条线,在3D平面上这就是一个2D平面...以此类推。
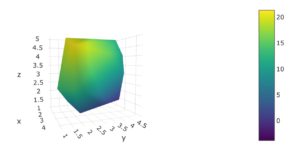
总之,现在学到的内容如下:
(不严谨的表达)
先讨论下面这个公式形成的空间:(为什么不是等号放在后面继续讨论)
[mathjax]A\boldsymbol{x}\leq \boldsymbol{b}[/mathjax]
先讨论有解的情况:
- 在[mathjax]N[/mathjax]维空间绘制一系列维度为[mathjax]N-1[/mathjax]的“超平面“
- 这些超平面相互约束形成一个解空间
- 这个解空间一定是convex的,空间任意2点连线一定在这个空间内部
- 先别管为什么一定是convex了,反正就是这个样子
然后讨论无解/无界解的情况:
无解:hyperplane平行
无界解:hyperplane不闭合,延伸至无限远的地方
然后继续讨论[mathjax]A\boldsymbol{x}\leq \boldsymbol{b}[/mathjax]和[mathjax]A\boldsymbol{x}=\boldsymbol{b}[/mathjax]两者之间的转换:
[mathjax]A\boldsymbol{x}\leq \boldsymbol{b}[/mathjax]到[mathjax]A\boldsymbol{x}=\boldsymbol{b}[/mathjax]:加入了松弛参数,引入了新的变量,提升了维度。目前的理解是simplex algorithm通过暴力提升维度去掉了[mathjax]\leq[/mathjax]和[mathjax]\geq[/mathjax]符号,用高维空间解决低维空间的问题。simplex algorithm发明于1946年,并不是什么17xx年/18xx年高斯、牛顿、拉格朗日时代的数学公式,而是一个目标为 computer friendly 的算法,目的是让计算机算起来开心。
🔗 [Math3d: Online 3d Graphing Calculator] https://www.math3d.org/
想用这个网页做一个“二维升到三维”的例子,但还没画出来(短时间内没找到添加1个松弛变量的二维例子...等待后续添加)
待续
降低计算量:解空间的顶点
继续:
现在我们有一个多维解空间,但还是找不到解在哪里,因为解空间内有无数个点。
一个很重要的定理(原文给出了reference,所以现在这个结论是可以直接拿来用的):如果确实有解,则解一定在这个“解空间”的某个“顶点”上。
也就是下面这张图上的橘黄色点。
First, if the maximum value exists within the solution space, then it will be on at least one of the polytope’s extreme points
https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm

现在计算量突然就降低了很多很多!
进一步减少计算量:顶点游走
但,仅仅是遍历计算这些”顶点“还是计算量太大了。我们要进一步降低计算量!
再来一个很重要的定理(原文给出了reference,所以现在这个结论是可以直接拿来用的)
如果解空间上的一个顶点不是最优点...那么它一定通过一条边,直接连向另一个顶点,那个顶点计算出来的数值更大(更优)...
但我们怎么知道某个顶点是不是最优点呢?
所以可以把上面这句话换一种方法表达:
如果解空间上的某个顶点直连的所有顶点都没有它计算出来的数值大...那么这个顶点就是最优点。
或者说:
只要通过一个限制很少计算量很小的检查条件(检查某个顶点直连的邻居顶点)就可以唯一确定整个解空间的全局最优解。
各种限制形成了多维解空间...解空间一定是凸多胞体...我们要的答案一定在这个解空间的某个顶点上...我们先选定一个顶点,然后不断移动,每次都向着“数值更大的邻居顶点”移动,最终就能找到那个唯一的最优解顶点。
If an extreme point does not give the maximum, then it has at least one edge to another extreme point such that [mathjax]\boldsymbol{c}^T \boldsymbol{x}[/mathjax] is strictly increasing along that edge.
So to find the maximum we first pick an extreme point and continually jump to neighboring extreme points with higher objective values until we reach one with no neighbors giving higher objective values. This point is a value of [mathjax]\boldsymbol{x}[/mathjax] such that [mathjax]\boldsymbol{c}^T \boldsymbol{x}[/mathjax] is maximized.
https://dando18.github.io/posts/2021/12/visualizing-the-simplex-algorithm
这个问题看起来简单了很多很多,但还有不少工作量可以做,一个直觉问题就是
(这些问题都写在继续学习simplex algorithm之前)
如何避免回路?
广度优先搜索?深度优先搜索?
如何找到一个更好的起始点使得计算量更低?
最后总结:前面提到的这些定理有中文版,来自🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892

过渡到下一篇要看的博客
继续读:(现在开始讨论simplex algorithm的矩阵实现)

写得有点短且难以理解,所以开始尝试看其他的博客
把这篇文章翻回来:🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892/
看到这里:
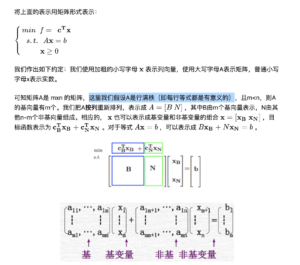
复习一些矩阵概念
线性无关
在线性代数里,向量空间的一组元素中,若没有向量可用有限个其他向量的线性组合所表示,则称为线性无关或线性独立(linearly independent),反之称为线性相关(linearly dependent)。例如在三维欧几里得空间[mathjax]R^3[/mathjax]的三个向量(1, 0, 0),(0, 1, 0)和(0, 0, 1)线性无关。但(2, −1, 1),(1, 0, 1)和(3, −1, 2)线性相关,因为第三个是前两个的和。
https://zh.wikipedia.org/zh-cn/線性無關
高斯消元法
高斯消元法
🔗 [高斯消去法 - 维基百科,自由的百科全书] https://zh.wikipedia.org/wiki/高斯消去法


增广矩阵
增广矩阵
接上面的高斯消元法,增广矩阵就是用来解线性方程的一种简化矩阵表达方法
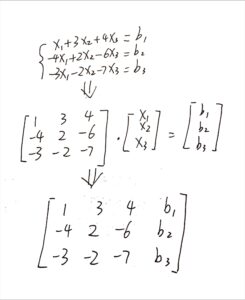
上面这张图最后一步的增广矩阵可以用高斯消元法继续化简为行阶梯的形式:
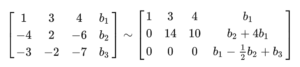
秩
秩(rank),满秩

早先的内容见🔗 [2021-10-12] https://truxton2blog.com/2021-10-12/
(这个链接也贴在2021-10-12里面)🔗 [一个矩阵列满秩意味着什么,能全面总结吗? - 知乎] https://www.zhihu.com/question/270393340

能懂,但细节有点糊,所以产生了一堆线性代数基础知识的小问题
临时记的几个小问题
有很多小问题,先写下来
✅为什么行秩和列秩一定相等
✅(回顾一下以前写的正交基笔记)
✅如果在一个矩阵里面藏一个正交基...
✅如果在一个矩阵里藏一个正交基,但还有很多其他的废物列(比如一个3x100的矩阵里藏了一组正交基,但还有很多很多其他列)
✅Ax=b在高维空间的移动:A是一堆向量,x是一堆指令,b是最终移动的终点
Ax=b有唯一解的情况(此时b是vector)是否还可以用正交基来表示(b变成正交基)
接上一条,似乎和矩阵的求逆有关...高斯消元法的wikipedia好像也提到了这个
矩阵的转置对应维度空间的什么变化?改变了维度的同时还改变了什么?
再复习一下行列式(Determinant)
对秩的一些混乱理解笔记
要不先看看这个
🔗 [06 - 逆矩阵、列空间与零空间_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1ys411472E?p=8
好像没有完全解决我的问题,继续看点别的
1:根据秩在空间里的直观表达...
秩=一个矩阵在对应维度空间里能够张开的最大维度
矩阵的行数=维度
比如3维空间里能产生:3维、2维、1维、零空间,但不能产生4维
这个矩阵处于二维空间:
[mathjax-d]\begin{bmatrix} 1 & 2 & 3 & 4 & 5 \\ 6 & 7 & 8 & 9 & 1 \end{bmatrix} [/mathjax-d]所以它肯定没办法张出一个3维空间来...Rank <=2
也就是说可以理解Rank一定[mathjax]\leq[/mathjax]行数(维度),也可以说Rank[mathjax]\leq[/mathjax]Row Number.
2:考虑这个:
这个矩阵位于5维空间...
[mathjax-d]\begin{bmatrix} 1 & 6 \\ 2 & 7 \\ 3 & 8 \\ 4 & 9 \\ 5 & 0 \end{bmatrix}[/mathjax-d]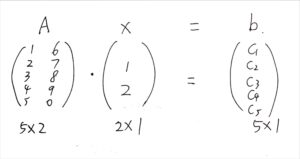
上面的内容解释为:
符号[mathjax]\boldsymbol{A}[/mathjax]是5维空间的2个向量...这2个向量最多最多形成一个二维平面。或者说,这2个向量相当于在这个5维空间里“运动”2次,无论怎么运动都最多形成一个二维平面。
符号[mathjax]\boldsymbol{x}[/mathjax]正在对上面提到的2个向量进行操作,或者说,相当于操作符号[mathjax]\boldsymbol{A}[/mathjax]代表的2次“向量运动”(方向是符号[mathjax]\boldsymbol{A}[/mathjax]提供的,距离是符号[mathjax]\boldsymbol{x}[/mathjax]提供的),最后确实能形成一个5维向量坐标,但这个坐标的取值范围有限。
有多有限?由于只“运动”2次,所以逃不过二维平面,解释为[mathjax]\text{Rank}(\boldsymbol{A})\leq 2[/mathjax].
也就是说“5维”在上面的例子里没有什么用,真正起作用的是“运动”的次数(决定了上限),所以认为Rank[mathjax]\leq[/mathjax]Column Number.
3:总结为:在一个高维空间里有m个高维空间向量(符号[mathjax]\boldsymbol{A}[/mathjax]提供的),这些高维空间向量要移动m次(每次移动m个向量中的一个并叠加方位)最终到达一个高维空间坐标。首先无论怎么移动都不可能破坏维度限制(Rank[mathjax]\leq[/mathjax]Row Number);其次,最终可能到达的位置形成的空间是有限的:移动1次最多形成一条线(1维);移动2次最多形成一个平面(二维)...所以Rank[mathjax]\leq[/mathjax]Column Number .
虽然说现在既有了Rank[mathjax]\leq[/mathjax]Row Number又有了Rank[mathjax]\leq[/mathjax]Column Number,但离最终结论[mathjax]\text{Row Rank}=\text{Column Rank}[/mathjax]还很远。严谨的证明见🔗 [为什么矩阵行秩等于列秩? - 知乎] https://www.zhihu.com/question/25524378
先不管行秩=列秩的严谨证明了,继续想点别的:
考虑到正交基这个东西,现在开始这样想:
现在我打算在矩阵里藏入一个正交基矩阵,让最终张开的空间维度最大化
比如:
[mathjax-d]\begin{bmatrix} 1 & 0 & 0 & a & b \\ 0 & 1 & 0 & c & d \\ 0 & 0 & 1 & e & f \end{bmatrix}[/mathjax-d]如果按“运动“的方法一列一列观察这个矩阵:
由第1、2、3列可知,这个矩阵往3个正交基的方向都运动过了,最终可能抵达的位置形成的空间一定是三维空间。虽然最终有可能回到原点(通过构造某些数值),但 可能形成的 空间一定是三维空间。
再想点别的:
假设现在考虑一个3x3的矩阵,考虑它的Row rank, Column rank对应的意义。
第一个例子:
当某一行被证明为“废物”(可以由另外两行线性组合而成)时,肯定有一列也是“废物”(可以由另外两列线性组合而成):

第二个例子:
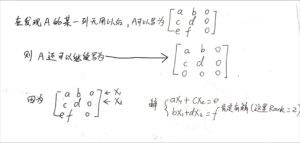
总结起来就是,在考虑Rank的时候,无论矩阵A是什么非方块的形状(行数大约列数,或者行数小于列数),根据上面的结论Rank[mathjax]\leq[/mathjax]Row Number并且Rank[mathjax]\leq[/mathjax]Column Number,它都可以“缩减”成一个方块矩阵进行考虑,方块矩阵的维度等于min(row, column);然后方块矩阵如果存在废物行/废物列(有废物行就是有废物列,等价的),则还可以进一步缩减成更小的方块矩阵,直到方块矩阵的维度等于原始矩阵A的秩为止。也就是说,虽然现在没有严谨证明,但确实可以直观理解为,行秩=列秩
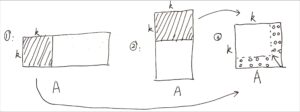
转置,秩,维度变化
为了直观理解 非方矩阵 的变换(比如转置)在空间上的意义(转置后如果降维还可以理解,但是升维呢?),再看看这个视频:🔗 [【熟肉】线性代数的本质 - 06补充说明 - 非方阵_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1ns411r7NX/
满秩的定义
对于m x m的方阵,full rank的定义很简单,就是Rank(A)=m -> 满秩
对于m x n的非方阵,full rank的定义是:Rank(A)=min(m, n) -> 满秩
如果从上面的一系列零散笔记看到这里,要强行直接接受这个结论也完全可以:
(这段内容不保证描述准确)一个5x2的(5维空间)矩阵转置为一个2x5的(2维空间)矩阵,它们代表的空间意义是一样的,有效的东西都只有2维。即使是5x2的矩阵看起来在5维空间,但张成的实际空间只有2维,这是column number限制的,因为只有2个基(2列),所以我们在某些时候还应该把它看作2维。无论是5x2还是2x5,它们都是满秩的,因为它们能张成的空间最多只有2维,所以评价为满秩也很合理。
换句话来说,一个2维空间的2x5的矩阵“升维”到5维空间,虽然用5维空间的坐标进行表示,但它实际拥有的东西仍然是2维。
再或者说,假设我们现在有一个Rank=2的2x2方阵,代表二维空间,我们给它添上很多0,变成一个100x2的矩阵,但它的Rank仍然没有变(甚至还是full Rank)...就算用100维坐标表示也是如此。
一些视频截图:
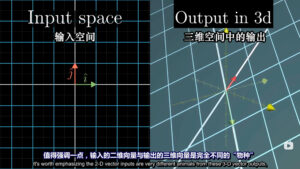


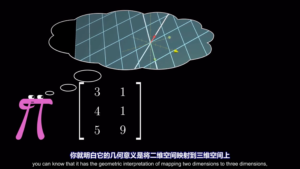
以及讨论一个3x2矩阵:
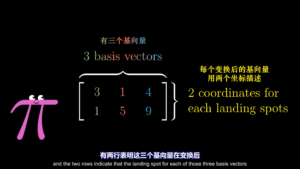
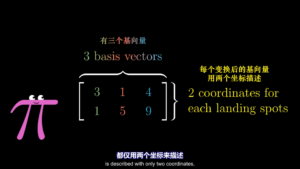

关于矩阵转置后“升维”,再考虑一个例子:
现在是Stellaris DLC 复仇女神版本,国家可以通过构建以太相位引擎来“升格”到虚境(称为灾飞),从而结束整个银河系的沙盘游戏。
假设一个弱小的国家是一个3x100的矩阵(3代表三维,100代表国力),强大的国家是一个3x500的矩阵(还是三维);要想灾飞到虚境,需要首先凑够1000的国力(通过以太相位引擎收集能量),变成一个3x1000的矩阵,然后进行矩阵转置:3x1000的矩阵转置后变成1000x3的矩阵,这样就“升维”到了更高位面。
然而瑞典蠢驴并没有告诉我们灾飞以后是什么样子,我们只能做一些猜测。一个可能的情况是,尽管国家灾飞到了虚境(1000维),但由于这些生物来自三维的银河系,所以这个国家即使是在1000维的虚境中也只是一个三维国家的样子而已。同时由于某些原因,整个国家的相对实力从1000变成了3(通过团结所有能量强行升维,在虚境中可能仍然很弱小)。以后到底有没有机会增加更多的列,从三维开始逐渐进化到1000维呢?没人知道。
再考虑一下”高纬度恶魔“(破界者)。作为三大终末危机的一个,它当然会给玩家带来很多麻烦。也许通过锚点源源不断进入银河系的那几百艘舰船,在它们来自的高纬度空间只有3个实体而已。3个实体代表高纬度空间的3列,通过矩阵转置以后变成了三维银河系的3行...等等,游戏中的高纬度恶魔恰好有3种颜色!

更多思考:一个3x2的矩阵或者2x3的矩阵(假定rank=2),都有看起来”多出来的“东西,计算机都要花额外的空间来存储这些”多出来的“信息。但这些信息在矩阵转置的时候都是必要信息(否则就会导致无法升维)
考虑如下“信息丢失”的问题:
假设现在有一个2x100的矩阵,它的200个元素都是用1~10000的随机整数填的(意味着“看起来”很有意义)。但这个矩阵的rank仍然为2,我们可以把100列中的98列全部消除变成0,这个矩阵看起来也没有变化。
但对计算机而言就不一样了,到底该存储哪个矩阵?存储原始的2x100矩阵,和存储处理后的”一堆0“的矩阵,代价一样吗?或者说,把原始矩阵的很多列消除为0以后,丢失的信息永远不可能复原了,那这一步(指消除列为0)该不该做?
当然不该。高斯消元法本来就是不可逆转的减熵过程。
秩与解空间的维度关系
解空间的维度 = 矩阵的列数 - 矩阵的秩
或者说:矩阵的秩 + 解空间的维数 = 方程组未知数的个数(🔗 [向量空间的维数等于对应矩阵的秩,那么为什么:矩阵的秩 + 解空间维数 = 线性方程组未知数的个数? - 知乎] https://www.zhihu.com/question/265713077)
最开始是在B.T.这本书的p43看到的:
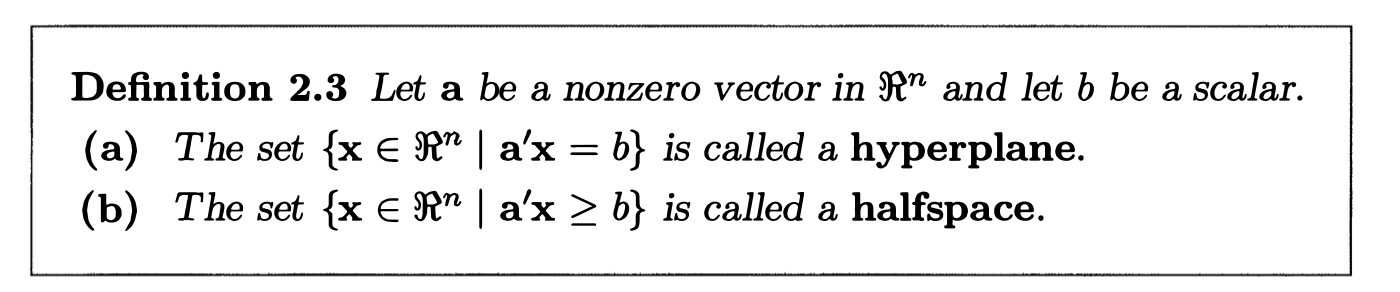
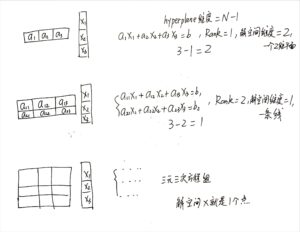
或者说:一个N维空间的hyperplane是一个N-1维空间。
以三维空间为例,三维空间的hyperplane是一个二维平面:
chatgpt
You:
三维空间中的hyperplane是指一条线还是一个二维平面?四维空间呢
ChatGPT:
在三维空间中,超平面(hyperplane)是指一个二维平面。理论上,一个n维空间中的超平面是一个(n-1)维的子空间。因此,在四维空间中,超平面则是一个三维的子空间。 举个例子,假设我们在三维空间中有一个坐标轴,我们可以通过任意点(不在原点)画一个平面,这个平面就可以被看作是穿过那个点的超平面。 同样的,在四维空间中,超平面就成了我们所理解的"三维空间",也就是说,它能够"切割"四维空间,形成两个分离的部分。
You:
如何用ax=b(b是scalar value)解释三维平面的hyperlane是二维平面
ChatGPT:
对于线性方程 ax = b,其中 a 是 n 维向量,x 是 n 维变量向量,b 是标量值,这个方程可以用来描述一个 n-1 维的超平面。 以三维空间为例,假设我们有方程 ax = b,这里 a = [a1, a2, a3],x = [x1, x2, x3],并且 b 是一个标量。那么这个方程就可以展开为:a1x1 + a2x2 + a3x3 = b。这个方程就描述了一个二维平面,也就是三维空间中的一个超平面。 为什么这样的方程会描述一个二维平面呢?因为在这个方程中,我们有三个变量(x1, x2, x3),但他们并不是完全独立的,他们需要满足一个线性关系(a1x1 + a2x2 + a3x3 = b)。因此,实际自由的变量只有两个,所以方程描述的是一个二维的平面。 同样的道理,如果我们在四维空间中,有一个线性方程 ax = b,这个方程将会描述一个三维的超平面。
You:
我更熟悉矩阵的秩,如何把上面这个解释用“矩阵的秩”表达
ChatGPT:
"矩阵的秩"是指一个矩阵可以被简化为的最大行列式的阶数。对于线性方程组,矩阵的秩可以告诉我们系统的解的自由度。 具体来说,如果我们有一个形如 Ax = b 的线性方程组,其中 A 是一个 m x n 矩阵,x 是一个 n 维向量,b 是一个 m 维向量。如果我们知道 A 的秩为 r,那么意味着有 r 个线性独立的方程在描述我们的系统。由于这 r 个方程是线性独立的,所以我们需要有 r 个信息或者说 r 个变量来唯一确定一个解。因此,我们说解空间是 n-r 维的。 所以,对于 ax = b 这样的单个线性方程(可以看作是一个 1xN 矩阵),矩阵的秩是 1,因此解空间是 N-1 维的,也就是一个 N-1 维的超平面。 特别的,当我们在三维空间中考虑一个线性方程 ax = b 时,由于这是一个线性方程,所以它的系数矩阵的秩是 1,因此它定义的是一个二维平面,这个二维平面就是三维空间中的一个超平面。同理,一个四维空间中的线性方程定义的超平面是三维的。
You:
等等,对于 ax = b 这样的单个线性方程(可以看作是一个 1xN 矩阵),矩阵的秩是 1,那为什么解空间是n-1维的
ChatGPT:
在一个线性方程系统中,我们说解空间的维度是由系统中的变量数目(矩阵的列数)减去矩阵的秩来确定的。 对于 ax = b 这样的单个线性方程,这是一个一阶线性方程,你可以把它看作一个 1xN 的矩阵。我们说这个矩阵的秩是1,因为我们有一个非零的方程(也就是一个线性独立的行)。那么,我们有 N 个变量(列),但只有 1 个线性独立的方程(行),所以解空间的维度就是 N - 1。 解空间的维度反映的是解的自由度。对于 ax = b 这样的单个线性方程,我们有 N 个变量,但所有这些变量都受到同一个方程的约束,所以变量之间并非完全独立,他们之间存在线性关系。实际上,我们可以任意选择 N-1 个变量的值,然后最后一个变量的值就由方程决定了。所以我们说解空间是 N-1 维的。
博客:简单理解线性规划的单纯形算法(zhihu.com)
part1
从这里继续看:
🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892

不需要学习新的知识,仅凭学习过的内容(要包括本笔记早先的内容,比如矩阵的行秩列秩)就可以理解这部分。
首先,我们要处理的问题是simplex algorithm,矩阵A的维度应该都是“row<column”的,否则仅凭矩阵A本身大概率就可以求解方程组了(求出唯一的解,且和min()/max()问题无关)。只有row<column,才会出现“未知数>方程数“,才会让我们在解空间上寻找最优解,min()或max()问题才有意义。
这也正是“加入松弛变量”带来的结果(把不等式变为等式,让矩阵的列数>行数)。
其次要注意,变换矩阵A的某些列以后,[mathjax]\boldsymbol{x}[/mathjax]也是要变换顺序的。
基解,可行解,基可行解
继续:
🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892
不需要学习新的知识,仅凭学习过的内容(要包括本笔记早先的内容,比如矩阵的行秩列秩)就可以理解这部分:

注意这张图中,“基解”未必都是“可行解”,是因为“基解”没有那堆 基变量 [mathjax]x_1,x_2,x_3,x_4\cdots x_m \geq 0[/mathjax]的限制条件.
举例:
基解:[mathjax][2,2,-1,-3,5, \vdots \ 0,0,0,0,0][/mathjax]
可行解:[mathjax][2,0,10,2,5, \vdots \ 0,0,2,0,3][/mathjax]
基可行解:[mathjax][3,5,10,2,9, \vdots \ 0,0,0,0,0][/mathjax]
上面的例子在以后的笔记(p=12250)里有了更新:

出基和入基
理解笔记
继续:
🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892
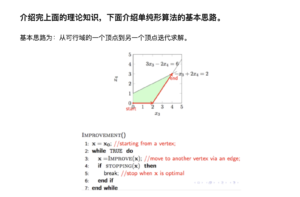

要看懂这部分的公式在做什么其实不难,找张草稿纸画一下就行了。但目前还是不知道为什么 出基/出基变量 要这么选。
有个前提要注意一下:

注意这里是“基本可行解”,而不仅仅是“可行解”:参考原博客对基本可行解的定义图。这个限制很重要,因为到了第3步你会发现[mathjax]\boldsymbol{x}[/mathjax]突然就被分成了两个部分,其中一个部分全都是0 .
此外还要注意的是,目前看来似乎求[mathjax]\lambda_{B}[/mathjax]的细节被省略了。目前看来,要想求[mathjax]\lambda_{B}[/mathjax],则又需要解一个新的[mathjax]\boldsymbol{A}^{\prime} \boldsymbol{b^{\prime}}=\boldsymbol{x^{\prime}}[/mathjax]方程,其中[mathjax]\boldsymbol{A}^{\prime}[/mathjax]是方块矩阵。现代计算机当然有一套自己的方法求解,也就是求[mathjax]\boldsymbol{A}^{\prime}[/mathjax]的逆。也就是套入这个公式即可:[mathjax]\boldsymbol{x}=A^{-1}\boldsymbol{b}[/mathjax] .
所以这个步骤简单描述就是:
先把一个非方形矩阵(m x n,其中n>m)“重新排列”[*注释*]成左右两部分,左边是一个m x m的方块矩阵且它的每一列都线性无关(Rank达到最大值m),左边的方块矩阵的每一列都称为“基向量”,右边剩下的部分的每一列都称为“非基向量”;
现在从非方形矩阵的右侧(非基向量区域)随机挑出一列,要用某种筛选方法,从左边的方块矩阵(基向量区域)里挑出一列,两列进行“交换”[*注释*]。
在非方形矩阵[mathjax]\boldsymbol{A}[/mathjax]“交换”列的同时,[mathjax]\boldsymbol{x}[/mathjax]也要对应的发生改变(重新计算数值,写在下一步)。
[*注释*]: 这个“交换”之所以打了双引号,是因为“交换”在草稿纸上更直观,然而计算机有可能并不会重新排布这个矩阵的列,而仅仅是用index记住“哪些列属于基向量,哪些列属于非基向量”。
再简单一点描述,到目前为止,(simplex algorithm)做的工作就是:不停的“重新排布”非方矩阵A的列,每次都让一列基向量“出基”,一列非基向量“入基“。
再保留一个问题等待后续解决:每次出基/入基以后还要保证左边的m列构成的方块矩阵的秩为m,应该是这样的吧?
chatgpt
在 Simplex 算法中,每次进行基变换(交换出基-入基的列)后,确保左侧的方块矩阵(称为基矩阵)仍然具有满秩是非常重要的。
Simplex 算法是用于线性规划问题的优化算法,其中包含一个线性约束矩阵,通常称为 A 矩阵。在每次进行基变换时,我们选择一个非基变量作为入基变量,并选择一个基变量作为出基变量。这涉及到对基矩阵的列进行变换。
基变换后,我们得到一个新的基矩阵。为了保持算法的有效性,新的基矩阵必须是满秩的。否则,它将导致问题的无解、无穷解或者算法无法继续进行下去。
因此,在 Simplex 算法中,每次进行基变换后,我们需要检查新的基矩阵的秩是否为满秩。如果新的基矩阵不是满秩,那么通常意味着需要进行进一步的调整或修正,例如重新选择基变量或者重新考虑约束条件,以确保问题的可行性和算法的正确性。
中途思考的问题
插入一个等待后续理解的问题:
在整个simplex algorithm矩阵运算中,哪些步骤代表了“在多维空间里,从一个顶点沿着一条边移动到另一个顶点”?
补充:这个问题最后解决了。事实上,整个simplex algorithm都在“从一个顶点沿着一条边移动到另一个顶点“,从一开始到最后得出最佳结果,全程都是。一开始就拿到了一个基本可行解保证这是一个”顶点“,同时在simplex algorithm迭代的每一步都保证了新迭代出来的[mathjax]\boldsymbol{x}[/mathjax]是一个基本可行解。
再插入一个等待后续解决的问题:

为什么这里能保证得到基本可行解,而不是可行解?(x的每一个元素都大约等于0一定成立吗)
补充:这个问题最后解决了。《最优化理论与算法》这本书讲的更好一些,
p39:

式3.1.11的[mathjax]x_k=[/mathjax]取了等号,这个等号保证了 一定 有一个原先的基变量变成了0(而不是“有可能变成0“).
出基和入基(2)
为什么这样出基入基就能优化?先不管了,继续:
🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892

...在非方形矩阵[mathjax]\boldsymbol{A}[/mathjax]“交换”列的同时,[mathjax]\boldsymbol{x}[/mathjax]也要对应的发生改变(重新计算数值)。
解释一下原博客附带的图:

在这张图里,一共4列蓝色(index从1开始算,第1、4、6、7列),这4列蓝色构成了基向量;绿色的列原本是非基向量(黑色),现在要和蓝色的某一列进行交换变成基向量。由于这里使用了index标记法(而不是重新排布列的组合)标记了基向量和非基向量,所以[mathjax]\boldsymbol{x}[/mathjax]只需要重新计算数值,不需要重新排列元素。尽管原博客并没有说明到底哪个基向量会被交换出去,但[mathjax]\boldsymbol{x}[/mathjax]的新数值还是可以先计算出来的,不会因为“选择哪一列进行交换”而改变。
遇到了理解不了的内容,准备换资料看
继续看:🔗 [简单理解线性规划的单纯形算法 - 知乎] https://zhuanlan.zhihu.com/p/31644892
下面这部分其实主要是在讨论这个问题:

选择入基变量:

开头的分块步骤划分出了一个全是0的区间,再次复习:基可行解,步骤1的初始解就是基可行解
目前最难理解的就是这一步:

到底是怎么从[mathjax]x^{\prime}_{j}[/mathjax]变成[mathjax]x_{j}[/mathjax]的???
当前我无法理解的地方在于,如果仅看最后一行,会发现最后一行的结果是确定的数值(而不是需要选取k构造出的一系列不确定的数值),而从[mathjax]x^{\prime}_{j}[/mathjax]变成[mathjax]x_{j}[/mathjax]的步骤似乎无法对应后面的“选取最佳判别数”,因为选取最佳判别数来自对矩阵A的计算。
另一个问题在于 ,从[mathjax]x^{\prime}_{j}[/mathjax]变成[mathjax]x_{j}[/mathjax],转换前后的分块[mathjax][x_B\ x_N][/mathjax]并不是位置一一映射的,而是要重新排列转换的!
求助一下博客参考的原书《最优化理论与算法》
似乎《最优化理论与算法》的步骤和博客不太一样(书中并没有把[mathjax]x^{\prime}_{j}[/mathjax]变成[mathjax]x_{j}[/mathjax]的步骤放在前面)
参考书《最优化理论与算法》P37~P40
完整PDF存档
帮助理解的最关键一步:对x_k的理解
《最优化理论与算法》P37, p38

(等待后续补充)这个地方的思路和zhihu.com的博客不太一样
仅仅看p38好像就搞明白了之前没懂的部分。先写点草稿怕忘了:

这一部分的内容大概是:
首先假设我们并没有什么基本可行解,我们也不知道该怎么优化。我们只是先观察一下整个公式,看看能不能找到什么规律:
(进行到这一步)
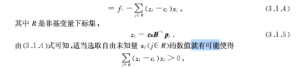
这个 有可能 其实是非常无奈且暗藏信息的。注意到我们一直在分析一个 一般情况下的 可行解[mathjax]\boldsymbol{x}= \begin{bmatrix} \boldsymbol{x_B} \ \boldsymbol{x_N} \end{bmatrix}[/mathjax],我们不能保证这里面的非基变量全都是0000000. 在这种强况下,想要突破一个复杂恶心的矩阵乘法并确保这个矩阵乘法得到的结果>0(只有>0才能优化),是非常困难的,有一大堆控制不了的东西要一个一个控制,远远超出了计算机的工作能力。
所以现在给出了一个强大的限制条件:基本可行解。基本可行解的非基变量都是0000000,它有一个好处就是:计算矩阵乘法的时候特别方便。如果全是0,我们直接秒得结果为0. 如果只有一个不为0的元素,我们只需要考虑这一个不为0的元素即可。就算这个[mathjax]\boldsymbol{x_N}[/mathjax]有几百维都不用怕了。
所以再给出一个大胆猜想,进一步控制条件:

蓝色标注的这一步(从现在学过的内容看来)非常大胆且有创造性。在基本可行解的强大000000基础上变一个非基变量,让一个混沌的(np-hard的)计算优化问题变成了可以在有限次里枚举的问题。
剩下的内容第一眼看起来不容易懂,但只要用草稿纸多画点图就不难理解。没有什么很难的知识点。

在这里要停一下。现在已经学到了基本可行解的强大,那么基本可行解(以及从基本可行解跳到一个更优的解)是否对应了多胞体的什么东西呢?
chatgpt
You:
现在我想用凸多胞体来想象一下simplex algorithm的步骤。我的问题是,“基本可行解”(非基变量都为0的可行解),是否对应了多维空间里,凸多胞体的一个顶点?从一个基本可行解到另一个(更优的)基本可行解,是否对应了“从凸多胞体的一个顶点,通过一条边,移动到另一个顶点”?
ChatGPT:
是的,你的理解是正确的。 在使用凸多胞体来想象Simplex算法的步骤时,基本可行解可以被看作凸多胞体的顶点。凸多胞体是由约束条件定义的凸多面体,而基本可行解是满足这些约束条件的解。非基变量为0意味着它们对应的顶点坐标为0,这使得基本可行解对应于凸多胞体的一个顶点。 在Simplex算法中,从一个基本可行解到另一个(更优的)基本可行解,确实对应于从凸多胞体的一个顶点通过一条边移动到另一个顶点。这是通过选择一个非基变量来增加(或减少)它的值,同时保持其他非基变量为0来实现的。这个过程可以看作是在凸多胞体的边上移动,因为在每个步骤中只有一个非基变量的值发生变化,其他非基变量保持为0。 通过这种方式,Simplex算法在凸多胞体上搜索,直到找到最优解对应的顶点。因此,你可以将Simplex算法的迭代过程理解为从一个顶点沿着边移动到另一个顶点,直到达到最优解。
虽然公式还没推完,但已经有了很大信心!现在终于知道这些步骤在做什么了。
对x_k的其他限制
继续看p39
很明显之前的步骤由于太过激动,漏掉了一个东西,它在p39被提到了:

这玩意([mathjax]\boldsymbol{x_k}[/mathjax])到底应该变成一个多大的正数?(在min()问题里是正数,在max()问题里是负数)


好像并不难理解。注意这一行公式:
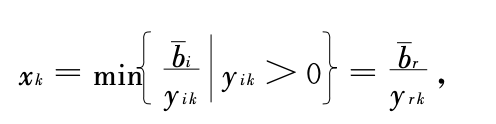
意思是,在所有[mathjax]y_{ik}[/mathjax]的集合中,只考虑[mathjax]y_{ik}>0[/mathjax]的情况,遍历所有[mathjax]y_{ik}>0[/mathjax]时[mathjax]\frac{\overline{b_i}}{y_{ik}}[/mathjax]的数值,最终统计[mathjax]\frac{\overline{b_i}}{y_{ik}}[/mathjax]的最小值。
由于构造[mathjax]\frac{\overline{b_i}}{y_{ik}}[/mathjax]集合的时候使用的限制条件是[mathjax]x_B\geq 0,\ x_{B_i}=\overline{b_i}-y_{ik}x_k\geq 0[/mathjax],所以最后,上一步的基本可行解[mathjax]\boldsymbol{x}[/mathjax]一定会发生这样的变化:
(因为这是基本可行解,所以注意[mathjax]\boldsymbol{x}[/mathjax]自身的特点:所有基变量都[mathjax]\geq 0[/mathjax],所有非基变量都等于0)
- 有且仅有一个基变量变成了0(这个基变量原来应该是>0的,但到底能不能[mathjax]\geq 0[/mathjax]还暂时存疑)
- 有且仅有一个非基变量变成了[mathjax]x_k\ (x_k>0)[/mathjax].
- 变换后的[mathjax]\boldsymbol{x}[/mathjax]不需要纠结新的基变量有哪些:那个从0变成[mathjax]x_k\ (x_k>0)[/mathjax]的(原)非基变量现在成为了基变量的一员;其他基变量成员保持不变;原先的那个基变量成员变成了非基变量。
- 第3步看起来很不严谨,怎么能保证新的[mathjax]\boldsymbol{x}[/mathjax]仍然是基本可行解?还要看p39剩下的一点内容。
迭代最后一步:交换(遗留一个小问题)
继续读p39:

但是...保留一点疑惑,写在下面:

红圈里的公式,尤其是这句话:

应该是(对后面的结论)非常有用的;但是暂时没想明白,所以等待后续有机会补充。
最开始我认为红圈里的公式并没有什么用,但随着我开始写笔记,我发现我并不能严谨的想明白“为什么新的m列线性无关“,所以目前认为红圈的内容有用,但我没想通。
有机会可以看看这些链接:
🔗 [linear algebra - Change of basis changes rank of matrix - Mathematics Stack Exchange] https://math.stackexchange.com/questions/3327031/change-of-basis-changes-rank-of-matrix
🔗 [matrices - Proof rank linear map is equal to the rank of its transformation matrix - Mathematics Stack Exchange] https://math.stackexchange.com/questions/3321902/proof-rank-linear-map-is-equal-to-the-rank-of-its-transformation-matrix
这部分内容是一开始想当然写的,有逻辑上的问题,所以埋了
红圈的这部分似乎并没有必要用到[mathjax]\boldsymbol{y}[/mathjax]。首先,“任何非基向量区域的列都可以用基向量线性表达“这是矩阵的秩的基本定理;其次,[mathjax]\boldsymbol{y}[/mathjax]甚至都是计算中途出现的产物(p38)。
但剩余的这句话还是非常有用的:

(不严谨证明时)可以这样想:假如置换两列以后,新的矩阵的秩只有m-1,新加入的列[mathjax]\boldsymbol{p}_k[/mathjax]肯定能用剩下的(m-1)列线性表达。然而并不可能,因为:这“剩下的”(m-1)列并不能线性表达置换出去的列[mathjax]{\boldsymbol{p_B}}_r[/mathjax](这是置换之前的矩阵的性质),要想线性表达置换出去的列[mathjax]{\boldsymbol{p_B}}_r[/mathjax],至少还要拉一个新的列进来,用m列才行。所以现在矩阵的秩又变成了m,而不是m-1.
单纯形法的终止条件
单纯形法的终止条件:
p39

simplex algorithm完整步骤
所以现在整个simplex algorithm的步骤就差不多了:

遗留的3个问题(解决了2/3)
继续上面这张图,但这里要注意一个细节:这个单纯形法的算法描述中并没有明显的提到该如何更新[mathjax]\boldsymbol{x}[/mathjax].
也就是这部分:

事实上[mathjax]\boldsymbol{x}[/mathjax]仍然是要更新的,只是放在了第一步,通过解矩阵方程的方法顺带更新了。
也就是说:
(书本上)通过这个方法探讨[mathjax]\boldsymbol{x}[/mathjax]对单纯形法优化过程的作用:“如果我把[mathjax]\boldsymbol{x}[/mathjax]的一个元素变动一下会怎么样“。在确定理论可行后,就不需要“主动”变[mathjax]\boldsymbol{x}[/mathjax],只需要“主动”变[mathjax]\boldsymbol{A}[/mathjax],然后顺便更新[mathjax]\boldsymbol{x}[/mathjax]即可。
停一下,还留了一个小问题:
如何在一开始得到一个最初的基本可行解?
似乎只需要先搞一个LU分解然后解一个矩阵方程就可以(细节就送给计算机吧),也就是这一步:

最后还留了一个问题来自本笔记中途出现的疑问:

几天以后,对参考书《最优化理论与算法》P37~P40的重新理解
为什么会有这部分笔记
过了几天,发现又记不牢simplex algorithm的一些细节了。
在上面的这些笔记(几天前的笔记)里,有一个关键节点,就是在《最优化理论与算法》看到这部分:

这部分内容可以说是整个simplex algorithm变换的核心,但也恰恰是这部分内容的结论过于简单易懂(只需要把[mathjax]x[/mathjax]的一个非基变量变成>0的数字就可以了...入基!),导致整个simplex algorithm的整体细节仍然没有完全弄懂。尤其是涉及[mathjax]z_j-c_j[/mathjax](reduced cost/判别数/检验数)的部分,以及涉及“交换“的部分(出基/入基的时候[mathjax]x[/mathjax]的其他元素怎么处理?[mathjax]x[/mathjax]的成员是要交换,还是仅仅记住基/非基的下标?[mathjax]A[/mathjax]要修改吗?[mathjax]A[/mathjax]是否也要进行更改,比如交换一些列的位置形成[mathjax]B-N[/mathjax]的结构?等等)。
所以费了很多时间,重新阅读了《最优化理论与算法》p37~p40(并把对应的PDF整个贴在了这篇笔记里面),并重新学习了本算法的过程。
矩阵与向量的变化
首先再次熟悉一些符号:
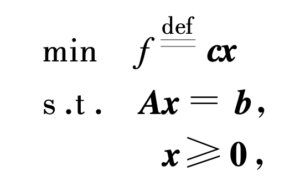
在接下来的过程里,这些矩阵/向量的变化大概是这样的:
[mathjax]A[/mathjax]从头到尾都是固定的,但[mathjax]A=(B, N)[/mathjax]这个所谓的标记是“人工挑选列对应的下标并记住的“(最开始产生[mathjax](B, N)[/mathjax]可能要搞点操作,但一旦确定以后就不需要再修改[mathjax]A[/mathjax]了)。也就是说,不存在什么”变换[mathjax]A[/mathjax]的列的顺序“这样的操作,从来都是”[mathjax]A[/mathjax]固定,但记住下标“的做法。
[mathjax]b[/mathjax]从头到尾都是固定的。
[mathjax]c[/mathjax]从头到尾都是固定的。
[mathjax]x[/mathjax]的变化方法是:从非基变量里挑出一个0变成>0,从基变量里挑出一个>=0变成0,其他基变量的位置不变,但全体基变量对应的数值会重新进行计算。出基-入基结束后,[mathjax]x[/mathjax]不需要重新排列,只需要记住基/非基的下标即可。例如:
[mathjax][3,5,10,2,9, \vdots \ 0,0,0,0,0][/mathjax]
(某一次出基-入基以后)变成
[mathjax][4,2,3,0,5, \vdots \ 0,3,0,0,0][/mathjax]
又在下一次出基-入基后变成
[mathjax][1,0,2,0,3, \vdots \ 0,5,0,2,0][/mathjax]
(注意到上面的每一步都更变了基变量的数值,这只是一个展示,目的是为了让自己搞清楚:并不是简单的交换两个数值就可以完成出基-入基的,其他基变量的数值都要重新计算的)
一些手写笔记
接下来是对《最优化理论与算法》p37~p40的完整笔记:
最重要的部分其实是对[mathjax]x_B[/mathjax]更新数值的理解。
错误的笔记:把x_B的变化理解为“简单的折线下压”
提醒:下面这部分笔记是一开始写的。其中最后的3张图带有一定误导性:把x_B的变化理解为“折线整体下压”,这其实是不对的。
把它理解为“折线从x轴的上方向下压,压到折线里的某个成员等于0为止“。这个动作决定了[mathjax]x_k[/mathjax]的大小应当如何设置。
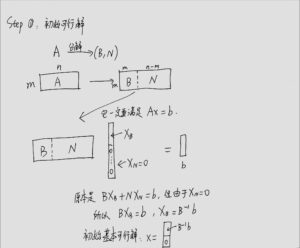

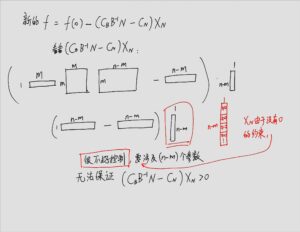
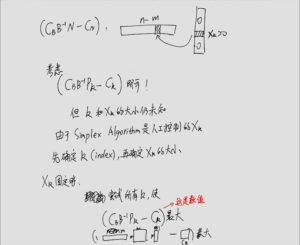
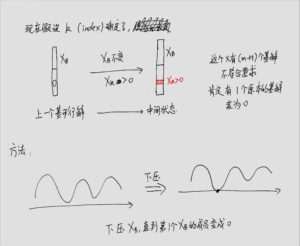

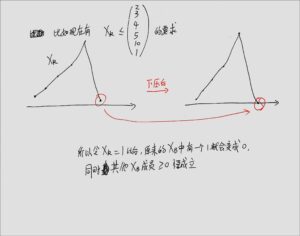
所以保留原本笔记的前4张图(去掉最后3张),并对x_B的变化重新解释:
原本的4张图:




还是考虑[mathjax]x_B[/mathjax]的变化:把它想象成一条“在x轴上方扭曲的蛇“
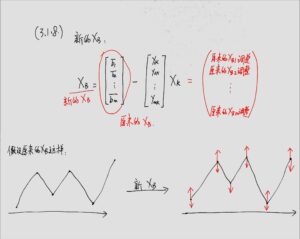
现在有一条蛇在x轴上方待命:当我们命令它动起来的时候,这条蛇的每一个点都有自己的想法(远离x轴,或者接近x轴),到底是远离还是接近,是由一系列[mathjax]y_{?k}[/mathjax]数值的正负决定的:

也就是说,当我们确定k以后,这条蛇的每个节点动起来的方向是确定的;我们只需要考虑这条蛇的那些“危险”节点(肯定会接近x轴的点),然后用于确定[mathjax]x_k[/mathjax]的大小,使得这条蛇在运动过后“恰好有一个点沾到x轴”即可。
注意到这条蛇的部分节点是可以远离x轴的,这个特性非常重要,因为在后面学习simplex algorithm对付degeneracy的时候我们又会考虑到...
比如我们现在处于一个基本可行解上,但这个基本可行解是退化的:
[mathjax][3,5,10,2,0, \vdots \ 0,0,0,0,0][/mathjax]
现在问题来了:从这个退化基本可行解出发,能否到达一个不退化的基本可行解?(不能回退)
比如说到达一个
[mathjax][2,4,8,0,3, \vdots \ 0,1,0,0,0][/mathjax]
如果用之前错误的“折线下压”的想法考虑问题,就会错误的认为“把一个非基变量0变成>0,肯定会导致原本基本量的0下压变成<0的数值...这样就不行了“。
可以试试p=12394这个例子,
事实上,从点F到点H,只需要重选pivot(换一个方法划分x的x_B和x_N)即可:

从min()切换到max()
《最优化理论与算法》p37~p40默认的场景时minimize(),如果变成maximize()该怎么思考?
大部分内容都是一样的,只需要在某些地方变一下正负号即可,更确切地说,只需要修改一个地方:判别数[mathjax]z_j-c_j<0[/mathjax].
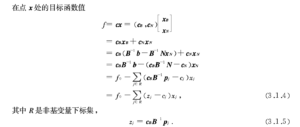
这个地方要想让新的[mathjax]f[/mathjax]比原来的[mathjax]f_0[/mathjax]更大,就需要通过某些策略,使得判别数[mathjax]z_j-c_j<0[/mathjax], 这样配上[mathjax]x_j>0[/mathjax]就可以让新的[mathjax]f[/mathjax]稳定增大了。
所以,
minimize():在一堆判别数里选出>0且最大的那个(如果没有>0的判别数那就最优解到头了)
maximize():在一堆判别数里选出<0且最小的那个(如果没有<0的判别数那就最优解到头了)
其他的地方,包括选取[mathjax]x_k>0[/mathjax]的策略,都不需要变。
