WARNING: This article may be obsoleteThis post was published in 2022-08-29. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今天从哪里开始？
昨天（2022-08-28）的笔记里学习了：
用一系列加权偏移单位冲激的响应来表示任意信号；
（线性系统）离散信号的卷积表示。
今天继续：
连续时间LTI系统的卷积积分
连续时间LTI系统的卷积积分
把离散和连续的公式写在一起对比：
离散时间LTI系统的卷积积分：
[mathjax-d]y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k][/mathjax-d]连续时间LTI系统的卷积积分：
[mathjax-d]y(t)=\int_{-\infty}^{+\infty} x(\tau) h(t-\tau) \mathrm{d} \tau[/mathjax-d]用卷积表示就是：
[mathjax-d]y(t)=x(t)*h(t)[/mathjax-d]例题
做一道例题就跑：
（求x(t)的响应y(t)的表达式）
糟糕，它的兄弟题（离散信号卷积例题2.3）放在昨天（2022-08-28）的笔记里了，现在重新拉到这篇笔记里来一起对比：
事实上，这两道题的解题步骤是几乎一样的。离散的那道题需要求等比数列的和，而这道题需要求[mathjax]e^{-a\tau}[/mathjax]的积分。
具体步骤就不再整理了，答案是：
[mathjax-d]y(t)=\frac{1}{a}(1-e^{-at})u(t)[/mathjax-d]* 这道题在我的（老版本信号与系统）PDF上出现了严重的扫描显示错误，不要看错答案了！
剩下的有关连续信号卷积和的题目就不做了。
LTI系统的一些性质
接下来是LTI系统的一些性质
由于接下来的性质基本上都和卷积相关，所以还是要写一遍卷积公式：
[mathjax-d]y[n]=a[n]*b[n]=\sum_{k=-\infty}^{\infty}a[k]b[n-k][/mathjax-d] [mathjax-d]y(t)=x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau[/mathjax-d]使用的符号风格和信号与系统的风格保持一致。这样做是为了加强印象，让自己以后不用查资料也能默写这个重要的公式。
对照：🔗 [卷积 - 维基百科，自由的百科全书] https://zh.wikipedia.org/zh-hans/卷积
交换律
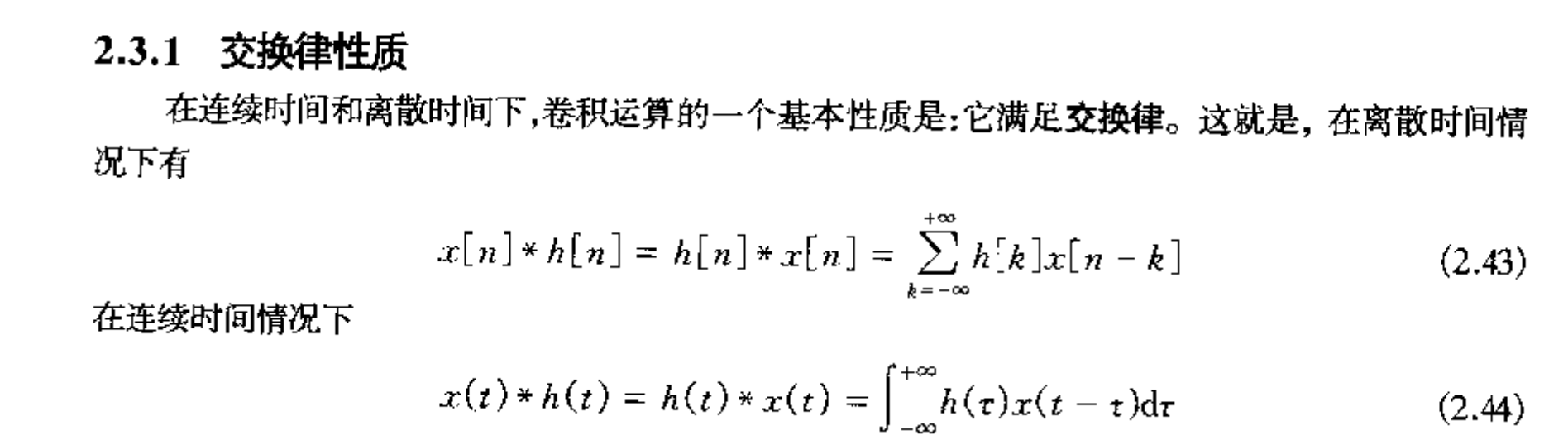
分配律
结合律
有记忆和无记忆LTI系统
（仅仅截了开头）
LTI系统的可逆性
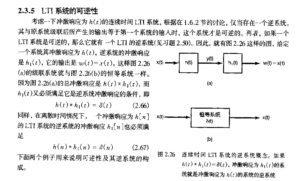
接下来还有一些特性，但暂时学不动了，准备跳过，以后有机会再来学。
补充：卷积的2种写法（交换律）
补充一个很重要的东西：卷积的2种写法
根据卷积的交换律，离散信号的卷积有2种写法：
[mathjax-d]x[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k][/mathjax-d]以及
[mathjax-d]x[n]=\sum_{k=-\infty}^{\infty}x[n-k]h[k][/mathjax-d]同样，连续信号的卷积也可以写成：
[mathjax-d]y(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau[/mathjax-d]以及
[mathjax-d]y(t)=\int_{-\infty}^{\infty}x(t-\tau)h(\tau)d\tau[/mathjax-d]周期信号的傅里叶级数表示
傅里叶级数到底是什么？
开始学这里：
P124 第3章 周期信号的傅里叶级数表示
先看看傅里叶级数到底是什么：
在数学中，傅里叶级数是把类似波的函数表示成简单正弦波的方式。更正式地说，对于满足狄利克雷定理的周期函数，其傅里叶级数是由一组简单振荡函数的加权和表示的方法。
https://zh.wikipedia.org/zh-hans/傅里叶级数
所以就可以直观看懂下面这个公式到底在干什么了：
（2023-08-27，在写p=12623草稿，学习 矩阵和微积分的关系 的时候补充，原始内容来自🔗 [從幾何向量空間到函數空間 | 線代啟示錄] https://ccjou.wordpress.com/2009/08/18/從幾何向量空間到函數空間/）
或者可以这样写：
[mathjax-d]f(x)=a_0+a_1\cos x + b_1\sin x+a_2\cos{2x}+b_2\sin{2x}+\cdots[/mathjax-d]其中，傅立叶级数的基底函数包含：
[mathjax-d]1, \cos{x}, \sin{x}, \cos{2x}, \sin{2x}, \cdots[/mathjax-d]为什么要把信号分解为傅里叶级数？
笔记：特征函数与特征值
P128
首先重新定义一些写法：
连续信号可以写为[mathjax]e^{st}[/mathjax]，离散信号可以写为[mathjax]Z^n[/mathjax]，其中[mathjax]s[/mathjax]和[mathjax]Z[/mathjax]都是复数。
接下先下结论：
注意：从现在开始使用一个更清晰的扫描PDF，所以页码会有所变化。
在掌握了卷积函数的交换律后，证明这个完全不困难：
需要特别注意上面这张图片里提到的 特征函数 和 特征值 。
需要记住的公式就是特征值：
信号[mathjax]e^{st}[/mathjax]对应[mathjax]H(s)=\int\limits_{\infty}^{+\infty}h(\tau)e^{-s\tau}d\tau[/mathjax]
以及
信号[mathjax]z^n[/mathjax]对应[mathjax]H(z)=\sum\limits_{k=-\infty}^{+\infty}h(k)z^{-k}[/mathjax]
结论写在最前面：
复指数是线性时不变系统的特征函数。(p114)
这样做有什么用呢？
当然上面这张图为了简化，忽略了一些细节，更完整的公式：
甚至可以这样说（注意：这条内容是自己记笔记的时候瞎想的）：对于[mathjax]a_1e^{s_1t}\twoheadrightarrow a_1H(s_1)e^{s_1t}[/mathjax]（箭头[mathjax]\twoheadrightarrow[/mathjax]代表 经过系统处理 ），我们发现[mathjax]a_1[/mathjax]是不参与特征值[mathjax]H(s_1)[/mathjax]的计算的！如果我们事先有一张表，存储了一系列高精度[mathjax]e^{s_1t}\twoheadrightarrow H(s_1)[/mathjax]的映射结果（就像正态分布查表一样），我们就可以把[mathjax]a_1e^{s_1t}\twoheadrightarrow a_1H(s_1)e^{s_1t}[/mathjax]这一步的计算量减少到几乎可以忽略不计，剩下的具有难度的任务就只剩下 分解 ：[mathjax]x(t)=a_1e^{s_1t}+a_2e^{s_2t}+a_3e^{s_3t} \cdots[/mathjax] .
也就是说：在上面这张图的步骤里，最关键的一步就是 分解 ，只要成功分解了，这个复杂的信号的响应就是非常容易求的！
例题
下面是一道例题：
P115
事实上这个例题并没有明确提出一个具体的问题，而是用这道题来验证一些学过的公式是成立的。为了自己不被绕进去，暂定这道题的问题是：求特征值[mathjax]H(s)[/mathjax]的表达式。
（注意第一张图里的红框，这一步很容易处理出错）
需要用到分部积分：🔗 [Integration by parts - Wikipedia] https://en.wikipedia.org/wiki/Integration_by_parts
[mathjax-d]\begin{aligned} \int_a^b u(x) v^{\prime}(x) d x &=[u(x) v(x)]_a^b-\int_a^b u^{\prime}(x) v(x) d x \\ &=u(b) v(b)-u(a) v(a)-\int_a^b u^{\prime}(x) v(x) d x \end{aligned}[/mathjax-d]
由最后一张笔记图片可知，我们可以用2种不同的方法来相互验证最终答案的正确性，这也就验证了前面学过的一些公式/性质的正确性。
连续时间周期信号的傅里叶级数表示
P116，继续学习：
大的要来了！
先把傅里叶级数（Fourier series）的公式写下来：
[mathjax-d]x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0t}=\sum_{k=-\infty}^{\infty}a_ke^{jk(\frac{2\pi}{T}t)}[/mathjax-d]这个东西很像以前学习的弦乐器正弦信号，或者称为harmonic series：
[mathjax-d]A4=0.8\cos(2\pi440t)+0.1\cos(2\pi880t)+0.05\cos(2\pi1320t)+ \cdots[/mathjax-d]注意这是连续信号，写成[mathjax]e^{j\omega t}[/mathjax]的形式以后它是一定是周期信号，所以可以转换：[mathjax]\omega=\frac{2\pi}{T}[/mathjax].
P118，注意到有这样的表达：
星号*的含义：🔗 [math notation - What does \$x^*(t)=x(t)\$ mean in signals and systems? - Electrical Engineering Stack Exchange] https://electronics.stackexchange.com/questions/469256/what-does-xt-xt-mean-in-signals-and-systems
所以说，如果x*(t)=x(t)，那么就意味着x(t)是个实信号。
P118，先理解这一部分：
笔记：
接下来把这部分读完：
上面这张图的最后提到了“将...与公式（3.25）进行比较”：
（3.25）：
[mathjax-d]x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0t}[/mathjax-d]比较：
[mathjax-d]x(t)=\sum_{k=-\infty}^{\infty}a_k^*e^{-jk\omega_0 t}[/mathjax-d]以及
[mathjax-d]x(t)=\sum_{k=-\infty}^{\infty}a_{-k}^*e^{jk\omega_0 t}[/mathjax-d]当然能看出
[mathjax]a_k=a_{-k}^*[/mathjax]，以及[mathjax]a_{-k}=a_{k}^*[/mathjax]（这两个等式其实表达的是一个同一个东西，就是共轭）
啊，这个其实就是 共轭 ，比如一个例子：
继续上面的内容，贴出更完整的公式：
其中，[mathjax]a_0[/mathjax]的出现原因可以参考这张草稿，如果一个复数的共轭等于它自己，那么它一定是实数。
其次，从公式（3.30）的上一步推导到3.30需要用欧拉公式展开复指数信号。
最后，用极坐标的形式表示复数[mathjax]a_k[/mathjax]是为了彻底在公式中消去 复数 这一概念，让公式里所有的元素都为实数。
完整公式（3.31）：
[mathjax-d]x(t)=a_0+\sum_{k=1}^{+\infty}A_k\cos(k\omega_0 t +\theta_k)[/mathjax-d]再对比一下一开始学习的傅里叶级数（3.25）：
[mathjax-d]x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0t}[/mathjax-d]以及2个更早的版本（3.13以及书本P115），但并不是傅里叶级数：
[mathjax-d]x(t)=\sum_ka_k e^{s_kt}[/mathjax-d] [mathjax-d]x(t)=\sum_k a_k e^{j\omega_k t}[/mathjax-d]以及最后，把（3.31）写成另一种形式（极坐标的笛卡尔坐标系写法[mathjax](a+bj)[/mathjax]）：
[mathjax-d]\displaylines{\text{let}\ a_k=B_k+jC_k\\ x(t)=a_0+2\sum_{k=1}^{\infty}(B_k\cos(j\omega_0 t)-C_k\sin(j\omega_0 t))}[/mathjax-d]对（3.31）进行解释：
[mathjax]a_0[/mathjax]是一个实数；[mathjax]A_k[/mathjax]为极坐标的Amplitude/模长，也是实数，和[mathjax]\theta_k[/mathjax]一起 “绑定” 了 复数平面/极坐标 上的一个点[mathjax]a_k[/mathjax]；总之，这个公式里面全都是实数！
对上面3个公式的解释：
从3.13到3.25，再到3.31，可以理解为一个“逐步假设、逐步简化应用场景”的过程（简化应用场景意味着缩小应用范围）。3.13的第一个公式把信号表示为复指数信号的叠加，这样做能够极大程度化简 求系统对复杂信号的响应 这个计算过程（LTI系统专属）。3.13的第一个公式（见P115）把上一个公式的“复指数信号”从[mathjax]e^{s_kt}[/mathjax]限定为[mathjax]e^{j\omega_k t}[/mathjax]（从复数[mathjax]s_k[/mathjax]限定为纯虚数[mathjax]j\omega_k[/mathjax]），但这个时候仍然不是傅里叶级数！（可以参考书本P115）只有 额外限定为谐波关系 后，[mathjax]e^{j\omega_k t}[/mathjax]才能被写为[mathjax]e^{jk\omega_0 t}[/mathjax]，此时一个复指数信号就多了一个特殊的称呼： 傅里叶级数 。3.31则是限定了3.25处理的信号为实信号，得出了一个更贴近现实世界的信号系统的公式。
接上一个步骤，转换一下笛卡尔坐标系（在这里就是复数坐标系[mathjax](a+bj)[/mathjax]）：
P119
总结上面学习的一些公式在本书中的地位
