WARNING: This article may be obsoleteThis post was published in 2022-08-15. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
WordPress数据库wp_posts爆炸
救命！我的Wordpress突然毫无征兆地出现了诡异的错误：
WordPress database error MySQL server has gone away for query INSERT INTO `wp_posts` ....这个错误几乎瘫痪了整个Wordpress：所有操作wp_posts的功能都会出错，wp_posts表中会出现duplicate的行。
最后通过恢复数据库备份救回来了，具体什么原因也懒得深究了。
只能靠猜了，出现这个毫无征兆的错误之前我在进行的一个操作是：在古腾堡Visual Editor里同时粘贴两张比较大的图片（以前我都比较有耐心，总是会等一张图片上传完成后再copy第二张），不知道是不是这个行为导致的错误。
自从这个错误发生以后，所有 一次性上传多张大图 这样的操作，我都会用wp-admin/upload.php执行（直接上传），而不是古腾堡Visual Editor粘贴（走浏览器API）。
python阶乘（scalar）
python阶乘（scalar）
>>> import math
>>> math.factorial(10)
3628800Latex数学符号对应表
收藏：
🔗 [Latex数学符号对应表 - 叮叮当当sunny - 博客园] https://www.cnblogs.com/dingdangsunny/p/12312966.html
inter-onset-interval, IOI
inter-onset-interval, IOI
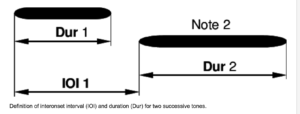
The corresponding term used in acoustics and audio engineering to describe the initiation of a sound is onset, and the interonset interval or IOI is the time between the beginnings or attack points of successive events or notes, the interval between onsets, not including the duration of the events. A variant of this term is interval of onset.
https://en.wikipedia.org/wiki/Time_point
论文阅读：Music Plus One and Machine Learning（只有一小部分）
《Music Plus One and Machine Learning》🔗 [Music Plus One and Machine Learning] https://music.informatics.indiana.edu/~craphael/papers/new_directions.pdf
二项分布相关的基础知识
二项分布相关的内容
啊，其实本质上是为了理解这个：
而不是为了彻底复习伯努利、二项分布等内容。
前置内容：
上一次涉及应该是在🔗 [2021-09-06 - Truxton's blog] https://truxton2blog.com/2021-09-06/，但没有详细记录
伯努利分布：🔗 [Bernoulli distribution - Wikipedia] https://en.wikipedia.org/wiki/Bernoulli_distribution
二项分布：🔗 [Binomial distribution - Wikipedia] https://en.wikipedia.org/wiki/Binomial_distribution
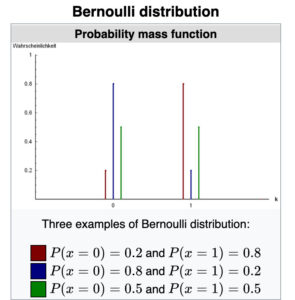
伯努利分布是简化版/特殊版的二项分布，用抛硬币的例子来说：
伯努利分布（Bernoulli distribution）：抛一次硬币的正反面分布（变成概率）。
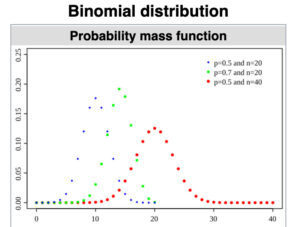
二项分布（Binomial distribution）：抛N次硬币，其中有x次为正面：这是一次实验，把本次结果（x）记录下来。然后重复【抛N次硬币】这个操作（N是固定数值），每次实验都记录对应的x数值。最终的X=x1, x2, x3...（集合）满足二项分布。
还有个负二项分布（negative binominal distribution）：目标是出现K次正面，一次一次的抛，直到第r次才达成这个目标：这是一次实验，把本次结果（r）记录下来。然后重复【抛r次硬币，直到出现k次正面】这个操作（K是固定数值），每次实验都记录对应的r数值。最终的R=r1, r2, r3...（集合）满足负二项分布。
二项分布和负二项分布的区别也可以见：🔗 [categorical data - Negative binomial distribution vs binomial distribution - Cross Validated] https://stats.stackexchange.com/questions/176034/negative-binomial-distribution-vs-binomial-distribution
有的时候会遇到这类表达式：[mathjax]{5}\choose{2}[/mathjax]，这其实是：二项式系数表达式：🔗 [Binomial coefficient - Wikipedia] https://en.wikipedia.org/wiki/Binomial_coefficient
其实在写Latex表达式的时候就已经学到了它的含义：
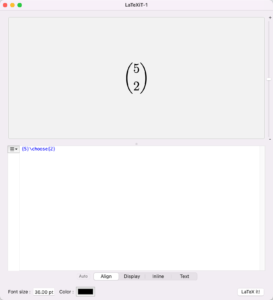
和熟悉的[mathjax]C_5^2[/mathjax]其实是一个东西，只是写法略有区别：
[mathjax-d]C_5^2 = {{5}\choose{2}}[/mathjax-d]负二项分布：
🔗 [负二项分布 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/负二项分布
当然还有二项式定理/Binomial theorem
🔗 [二项式定理 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/二项式定理
[mathjax-d](x+y)^n=\left(\begin{array}{c}n \\0\end{array}\right) x^n y^0+\left(\begin{array}{c}n \\1\end{array}\right) x^{n-1} y^1+\left(\begin{array}{l}n \\2\end{array}\right) x^{n-2} y^2+\cdots+\left(\begin{array}{c}n \\n-1\end{array}\right) x^1 y^{n-1}+\left(\begin{array}{l}n \\n\end{array}\right) x^0 y^n[/mathjax-d]比如
[mathjax-d](x+y)^4=x^4+4 x^3 y+6 x^2 y^2+4 x y^3+y^4[/mathjax-d]多项式系数有关的概率推导
参考资料
如何理解
首先列举所有有用的参考资料：
🔗 [mathematical statistics - Does a mixture model need to sum or integrate to $1$? - Cross Validated] https://stats.stackexchange.com/questions/277075/does-a-mixture-model-need-to-sum-or-integrate-to-1
🔗 [Combination - Wikipedia] https://en.wikipedia.org/wiki/Combination
🔗 [Multinomial theorem - Wikipedia] https://en.wikipedia.org/wiki/Multinomial_theorem#Ways_to_put_objects_into_bins
🔗 [计数原理3.2 多重排列 多项式定理 - 知乎] https://zhuanlan.zhihu.com/p/53499062
🔗 [多项式系数及其妙用] https://zlearning.netlify.app/math/probability/afcp-01dot5-multinomial-coefficients
注意最后一个链接，非常有用：
接下来就可以理解这个公式了：
发神经
在时刻t（frame单位），我的任务是：判断当前的频谱图属于哪个Note.
但我不知道该如何下手，所以我先解决第一个问题：判断当前的频谱图属于Note A4的概率有多大。
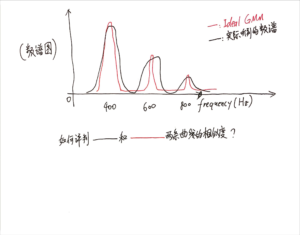
首先是一些引导笔记：
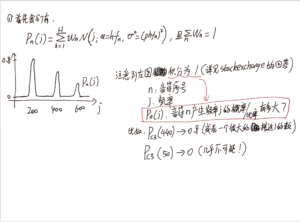
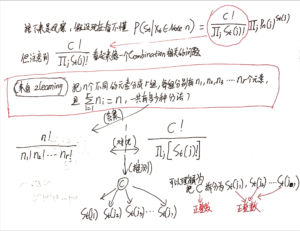
接下来用一个场景来理解这个问题：
祂给了我一个很大的常数C，并告诉我：你去把这个常数C分给20~20000Hz的每一个整数频率（可以分配0），分配的数值越多，代表这个频率的分量越大。现在你能不能把那个频谱图近似地表现出来？
当然可以。祂给我的C越大，我越能够近似地用离散数值表现出原来的频谱图。
分好了！
现在祂问我：刚才给你的这个常数C，你一共有多少种方法给它分好？
有这么多种：[mathjax]\frac{C !}{\prod_{j} s_{t}(j) !}[/mathjax].
等等，那个[mathjax]s_{t}(j)[/mathjax]是什么？
是非0的正整数！这样就可以衔接这个例题了。
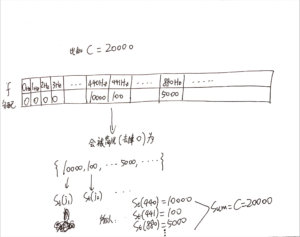
现在，我要设想一个新的场景：抽球。每当我抽出一个球，我会先把它交给祂，祂会在球的表面写下一些文字，然后交给我进行统计。
按照之前的说法，祂给了我C个球，我用这C个球拼凑出了频谱图的样子：
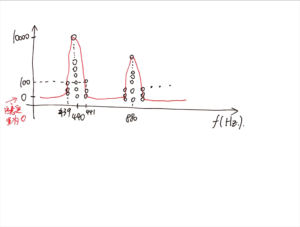
接下来我要逐一抽出（并交给祂进行标记）这C个球：
假如我的第一个球位于98Hz的地方，我把这个球交给了祂，祂写下了这些文字：
不是A4
我的第二个球位于439Hz的地方，我把这个球交给了祂，祂写下了这些文字：
是A4
我的第三个球位于439Hz的地方，我把这个球交给了祂，祂写下了这些文字：
是A4
...
直到所有的球都交给祂进行了标记。最后我开始统计写有 是A4 的球的个数，个数越多，说明当前频谱图越接近A4的频谱图。
等等，祂是根据哪条规定写下 不是A4 和 是A4 的？
根据概率！当我把98Hz的球交给祂的时候，祂会进行概率查询：[mathjax]P_n(j=98), n=A4[/mathjax]，然后根据概率的大小随机给我写上标记。
很容易想象，理想GMM建模下的音符A4几乎没有任何可能产生98Hz的频率分量！
所以说上面的这个抽球动作，本质上是一个伯努利试验，是吗？
是的！只是现实世界中我们已经知道了祂给球写上标记的概率依据，我们要做的只是求出一个具体的概率（而不是统计祂给我们标记了多少个球）。
再用一些计算举例来加深印象：
（判断A4）
我的频谱图几乎全集中在98Hz和196Hz上面了（20000个球，给98Hz分配了15000个，给196Hz分配了5000个），这个频谱图和A4的相似度是多少？（这里的0.000....01是随便取的，反正很接近0就对了）
[mathjax-d]\frac{20000!}{15000!5000!}*(0.00000001^{15000})*(0.0000002^{5000})[/mathjax-d]很接近0，对吧？再来看一个例子：
我的频谱图几乎全集中在440Hz和880Hz上面了（20个球（太多了算不动），给440Hz分配了19个，给880Hz分配了1个），这个频谱图和A4的相似度是多少？（这里的概率也是随便取的，最后的概率肯定不是真实的，但和上一个例子放在一起对比就可以看出很大区别了）
[mathjax-d]\frac{20!}{19!1!}*(0.95^{19})*(0.05^{1})=0.3773536[/mathjax-d]所以最后终于可以理解这个公式了：
[mathjax-d]P\left(s_{t} \mid x_{t} \in \operatorname{note} n\right)=\frac{C !}{\prod_{j} s_{t}(j) !} \prod_{j} p_{n}(j)^{s_{t}(j)}[/mathjax-d]遗留的2个思考题（解决了一个）
遗留的2个思考题（第一个似乎已经解决了，第二个看起来不会影响对论文的阅读）：
1：这一步可不容易，具体是怎么算的？
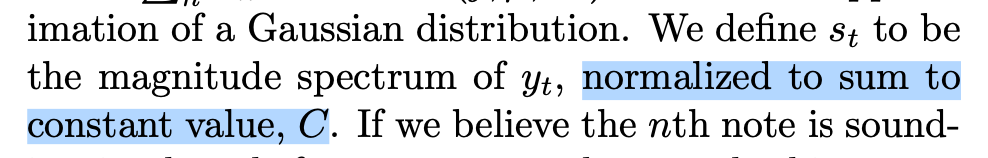
都是离散值，应该非常容易算，完全用不上积分。不要忘了积分的原始定义之一：用小长方形的面积去近似：
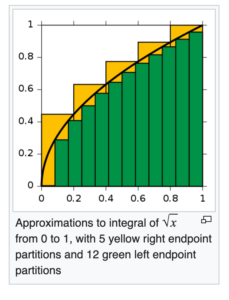
理想模型GMM倒是需要用积分计算，但那个完全不难，可以提前算好。
2：从之前的例子就可以看出，C很重要，但恐怕无法取过大的数字，那么到底应该用什么粒度来划分C？
在之前的例子里我默认使用了1Hz，然后根据0~20000Hz的范围划分出了C=20000
当然，目前看来>5000Hz的频率应该是用不上的（这里处理的是乐器的声音，而不是人耳听力范围），此外高频范围（比如说>2000Hz）的划分会比较稀疏。总的来说有机会把C压缩到5000以下。
接下来的内容
接下来的内容里似乎没有太多新公式和新知识。主要涉及的内容有kalman filter。作者使用了2种Normal distribution变量来控制对音乐演奏的建模，其中一个控制快慢（演奏的快慢），还有一个控制停顿（两个note之间可能会有人为停顿，停顿时间可能和乐谱无关）。
草稿如下：（大部分时间都用不上这张草稿）
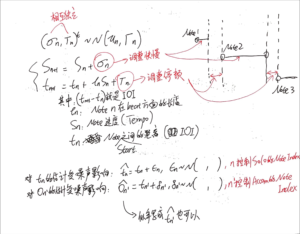
我也不知道这是什么
这篇笔记是2023年6月从档案库里捞出来的，我已经忘记当时为什么要写这些东西了，它们可能是待学习的知识：
推导markov
待补充
经验贝叶斯
