WARNING: This article may be obsoleteThis post was published in 2022-08-07. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
今天从哪里开始？
今天从哪里开始？
Kalman filter
更具体一点：从协方差矩阵的计算开始
昨天的笔记里，通过学习b站的视频，了解到了一个用kalman filter计算小车匀加速运动的例子，但是这个例子只进行到80%左右就结束了，导致我没有完全理解它。
今天继续，但从另一个网站开始（同样使用了类似小车匀加速的案例）：🔗 [卡爾曼濾波] https://www.kalmanfilter.net/CN/default_cn.aspx
学习kalmanfilter.net
alpha-beta-gamma滤波器
🔗 [alpha - beta - gamma 滤波器] https://www.kalmanfilter.net/CN/alphabeta_cn.html.
* 注意：下面的几个例子都属于[mathjax]\alpha-\beta-(\gamma)[/mathjax]滤波器，不是kalman filter！
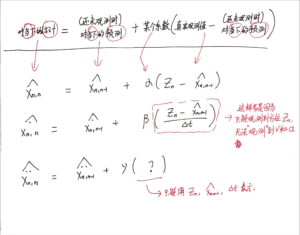
关键内容：用一个比小车匀加速更简单的场景推导出状态更新方程（尽管场景和滤波器不是kalman，但推导出的方程是kalman filter的一部分）：
继续学习，接下来学习了另一个案例：
下一个例子：匀加速飞机追踪：
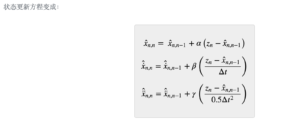
总结一点小技巧，以及推导过程（4张）：
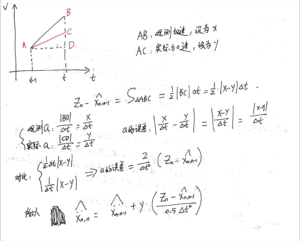
上面学的这几个例子（恒重金条，匀速飞机，匀加速飞机）都属于[mathjax]\alpha-\beta-(\gamma)[/mathjax]滤波器，下面是对这种滤波器的总结：
其中蓝色高亮的部分可能是这个滤波器最重要的性质。
然后再次回顾状态更新方程：
kalman filter的5个基本方程
接下来学习：🔗 [Kalman Filter in one dimension] https://www.kalmanfilter.net/kalman1d.html
哎呀，没有中文翻译了，只能看英文原文了。
接下来学习了第3个方程：
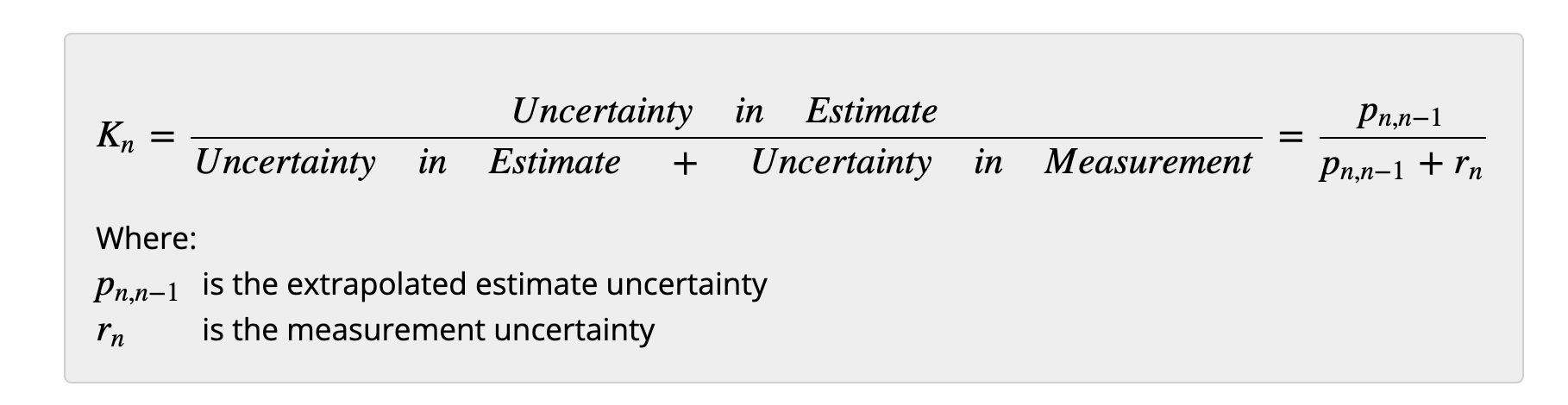
接下来学习第4个方程，它的计算需要用到第3个方程所得的kalman gain：
第5个方程：暂时还有点疑惑，先摆在一边：
接下来回顾5个kalman filter方程：
下面是一些笔记：
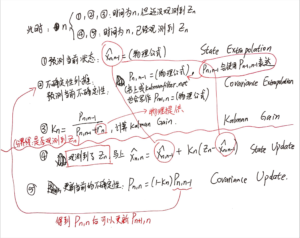
kalman filter总流程
kalman filter总流程：
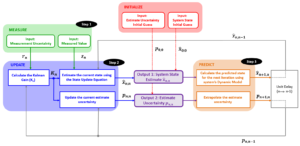
简化版笔记：
(和上面那张图可能有一点不同，但总体思路是一样的)
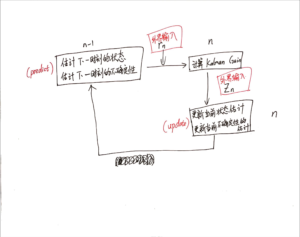
值得注意的是，最开始初始化模型以后马上就开始预测下一时间的状态了，这个步骤看起来和之前学bayesian filtering的初始化略有不同。
kalman filter的停止条件
kalman filter的停止条件
一直不停地滤波，有没有什么参数可以判断模型的收敛？
等等！好像有点不对。我们确实可以保证从[mathjax]P_{n,n-1} \leq P_{n,n}[/mathjax]，但执行Covariance Extrapolation（从[mathjax]P_{n,n}[/mathjax]到[mathjax]P_{n+1,n}[/mathjax]）的时候就一定能保证[mathjax]P_{n+1,n} \leq P_{n,n}[/mathjax]？
似乎确实如此，在后面一些的例子里（测量水箱的水温）就出现了[mathjax]P_{n+1,n} > P_{n,n}[/mathjax]的情况（这里引入了噪声）：
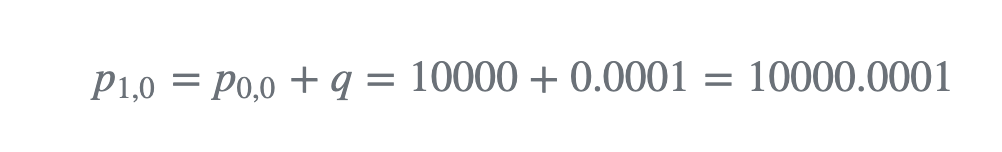
杂乱的内容：kalman gain的直观解释, lag error
基本步骤了解了，现在开始学习一些细节：
对kalman gain的直观解释：
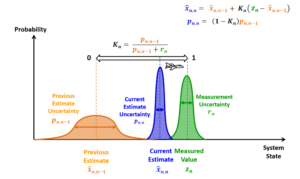
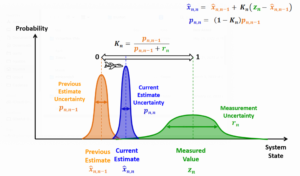
kalman gain的证明
🔗 [One-dimensional Kalman Gain Derivation] https://www.kalmanfilter.net/KalmanGainDeriv.html
注意到这一步：
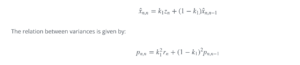
这里使用了这个公式：（来源）
[mathjax-d]\operatorname{Var}[\mathrm{kX}+\mathrm{c}]=\mathrm{k}^{2} \cdot \operatorname{Var}[\mathrm{X}][/mathjax-d]再注意到这一步：
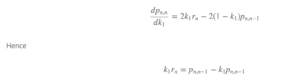
这一步的本质是：令导数为0求最优解：
[mathjax-d]\frac{dp_{n,n}}{dk_{1}}=0[/mathjax-d]现在开始做一道例题：测量建筑高度
并不难，和之前学过的「金条称重」类似，但多了一个区别：此时不仅会考虑estimate uncertainty，还会考虑measurement uncertainty.
其中estimate uncertainty和kalman gain会不断变化。
现在添加噪声影响，具体影响在这个公式：（注意下面的公式是由物理系统决定的，不同场景下的公式不一样）
[mathjax-d]p_{n+1, n}=p_{n, n}+q_{n} \ \ \ ( *\text{constant dynamics only}*)[/mathjax-d]lag error
留到后面再总结
这里有一个很严重的问题：我怎么知道我出现lag error了？
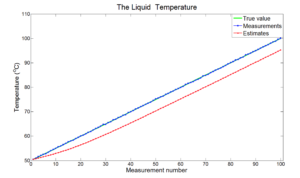
如上图所示，到达一定迭代次数后，lag error变成了一个constant，那我该如何判断？
（待补充）
（注：该想法未经资料证实）目前想到的唯一方法就是观察kalman gain的大小：如果太小，kalman filter就变成了以推测结果为主、观测结果为辅的模型，似乎失去了原本的作用和意义。
继续看下一章：
🔗 [Multidimensional Kalman Filter] https://www.kalmanfilter.net/kalmanmulti.html
协方差、协方差矩阵的计算（附带例题）
接下来开始进入带有矩阵推导的部分，先看一些基本数学公式：
🔗 [The background break] https://www.kalmanfilter.net/background2.html
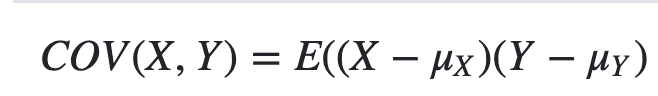
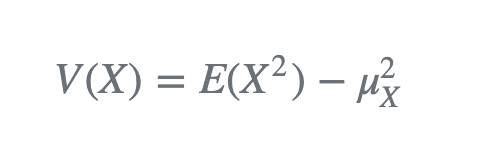
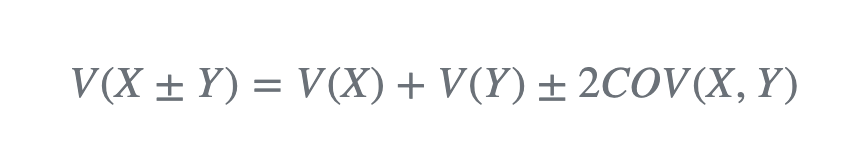
此外还有一个来自wikipedia的总结：
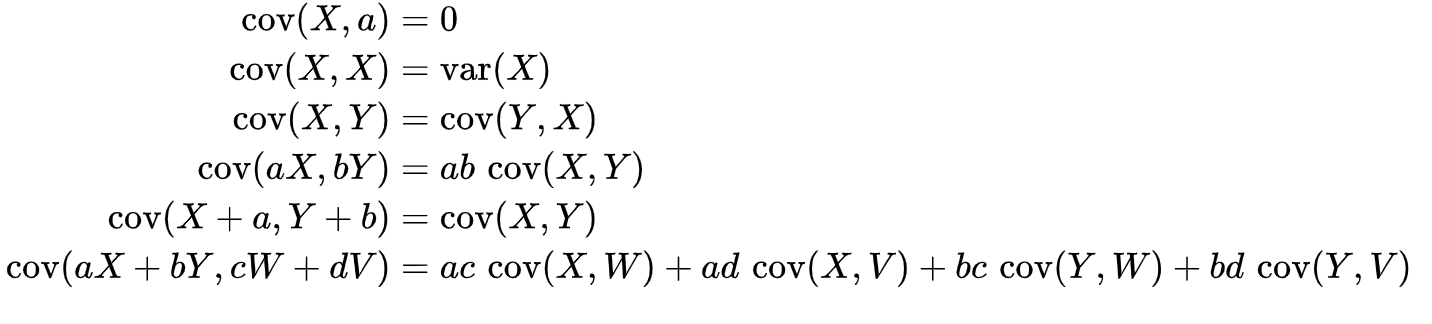
公式看起来都不难推导，但一做起真实数据的题就头大，需要再学习巩固一下：
非常令人恼火，一直没能够找到什么好用的资料（我需要SOLID EXAMPLE！！！）
勉强找到了，先凑合用吧：搭配下面2个链接：使用第一个链接（wikipedia）的公式做第二个链接（CSDN）的题目
🔗 [协方差矩阵 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/协方差矩阵
注意：这个例题里计算variance使用了n而不是n-1 🔗 [协方差矩阵的解法和例题拔牙的萌萌鼠的博客-CSDN博客协方差矩阵的求法例题] https://blog.csdn.net/Harry_Jack/article/details/109280048
注意：可以使用2种方法进行计算：
再补充一道例题：
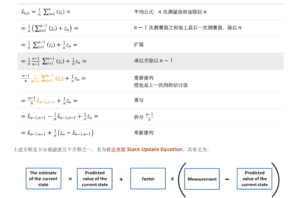
（来源）已知[mathjax]X=\{3,2\}, Y=\{7,4\}[/mathjax]，求X和Y的协方差以及协方差矩阵。
答案：
covariance: 1.5
[mathjax-d]\Sigma=\left[\begin{array}{cc} \frac{1}{2} & \frac{3}{2} \\ \frac{3}{2} & \frac{9}{2} \end{array}\right][/mathjax-d]关键过程：
