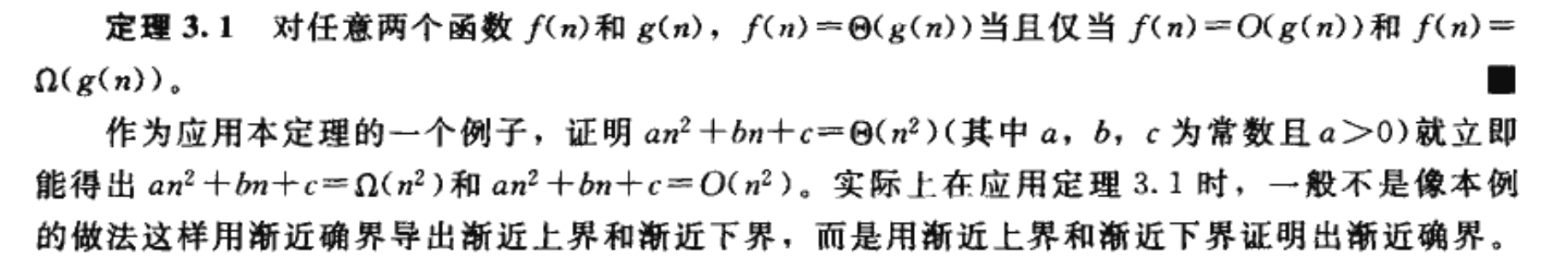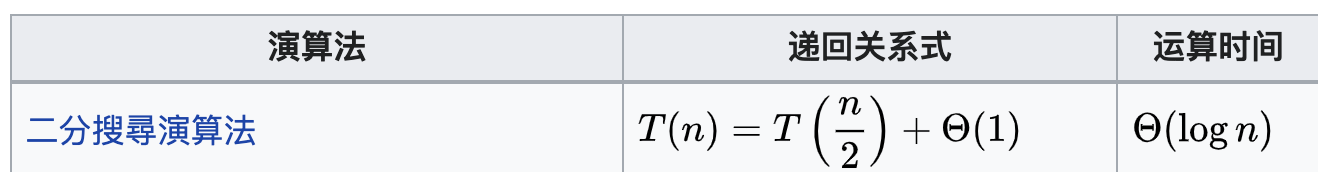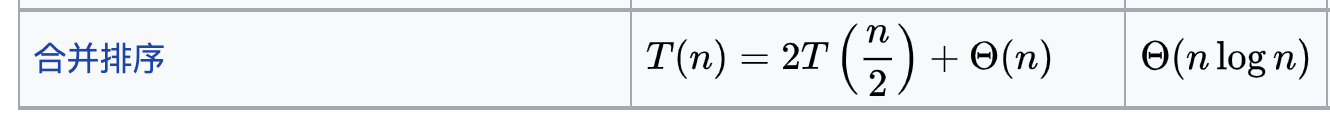This post was published in 2021-10-18. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
等差数列求和公式
🔗 [等差数列 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh/%E7%AD%89%E5%B7%AE%E6%95%B0%E5%88%97
有等差数列形式如下:
[mathjax-d]{\displaystyle \{a\,,\,\,a+d\,,\,\,a+2d\,,\,\cdots \,,\,\,a+(n-1)d\}}[/mathjax-d]则求和公式为:
【一个等差数列的和,等于其首项与末项的和,乘以项数除以2。】,也就是:
[mathjax-d]S_n=a n+d \cdot \frac{n(n-1)}{2}[/mathjax-d]等比数列求和公式
🔗 [等比数列 - 维基百科,自由的百科全书] https://zh.wikipedia.org/zh/%E7%AD%89%E6%AF%94%E6%95%B0%E5%88%97
有等比数列形式如下:
[mathjax-d]\left\{a, a r, a r^{2}, \cdots, a r^{n-1}\right\}[/mathjax-d]则求和公式为:
[mathjax-d]S_{n}=\frac{a\left(1-r^{n}\right)}{1-r}[/mathjax-d]python ++i和i++
🔗 [Python 为什么不支持 i++ 自增语法,不提供 ++ 操作符? - 知乎] https://zhuanlan.zhihu.com/p/149878104
二分查找/二分搜索
算法:时间复杂度
● 渐进时间复杂度:
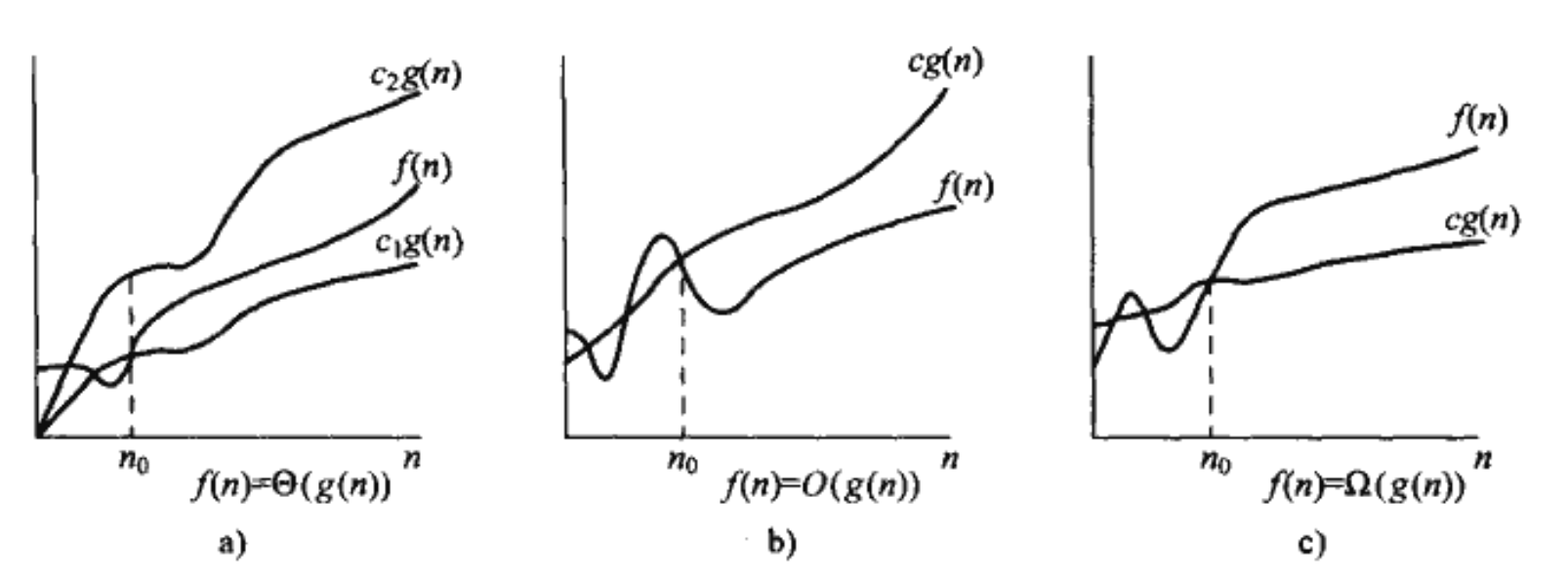
● 表示时间复杂度的不同符号:
具体内容见中文算法导论p26开始
● 关于[mathjax]\Theta[/mathjax]的例题:
● 特别要注意这个例题带来的重要条件:
[mathjax]\Theta(g(n))[/mathjax]的定义需要每个成员[mathjax]f(n)\in \Theta(g(n))[/mathjax]都是渐进非负。
● 有关[mathjax]O[/mathjax]:
注意[mathjax]f(n)=\Theta (g(n))[/mathjax]隐含着[mathjax]f(n)=O(g(n))[/mathjax],因为[mathjax]\Theta[/mathjax]记号强于[mathjax]O[/mathjax]记号。
● 有关[mathjax]O[/mathjax]记号和[mathjax]o[/mathjax]记号:
[mathjax]o[/mathjax]表示【非渐进紧确的上界】,详细内容见中文算法导论p30
取整和取模(mod)
详细内容见中文算法导论p32
● 下取整:[mathjax]\lfloor a \rfloor[/mathjax];上取整:[mathjax]\lceil a \rceil[/mathjax] .
● mod:
[mathjax]a\ mod\ n[/mathjax] 表示:[mathjax]a/n[/mathjax]的余数。
如果[mathjax](a\ mod \ n)=(b\ mod \ n)[/mathjax],那么这个表达式也可以写作:[mathjax]a\equiv b(mod\ n)[/mathjax].
算法:有关时间复杂度的计算(例题)
有关递归:(链接里还有其他复杂度计算例题)🔗 [算法的时间复杂度分析题笔记] https://www.shellcodes.org/Programming/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95/%E7%AE%97%E6%B3%95%E7%9A%84%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%E5%88%86%E6%9E%90%E9%A2%98%E7%AC%94%E8%AE%B0.html
对于某些形式的递归表达式,可以用更快速的方法解答:main theorem/master theorem/主定理,见下面
算法:使用 main theorem/master theorem/主定理 计算时间复杂度
(有定理推导和例题)🔗 [主定理 Master Theorem - 知乎] https://zhuanlan.zhihu.com/p/100531135
主定理公式:
例题:
应用:
❗另一个应用(需要仔细思考为什么merge sort对应这个推导式):
(可能需要再次回顾merge sort: 🔗 [2021-10-17 - Truxton's blog] https://truxton2blog.com/2021-10-17/ , 或:🔗[python归并排序--递归实现 - 简书] https://www.jianshu.com/p/3ad5373465fd )
python 优先队列/priority queue
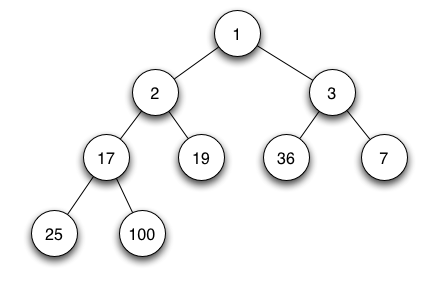
这个其实就是已经接触过的最小堆min heap/最大堆max heap:
在python中的实现(python heapq用的是最小堆,见:https://docs.python.org/3/library/heapq.html(网页内搜索“max heap”)):
from heapq import *
heap = []
insert = [10, 9, 8, 7, 6, 5, 4]
for item in insert:
heappush(heap, item)
while len(heap) != 0:
print(heap)
print(heappop(heap))
结果:
[4, 7, 5, 10, 8, 9, 6]
4
[5, 7, 6, 10, 8, 9]
5
[6, 7, 9, 10, 8]
6
[7, 8, 9, 10]
7
[8, 10, 9]
8
[9, 10]
9
[10]
10python 快速排序/quicksort
📚 具体内容见中文算法导论p85开始
(❗注意:这个例子里的细节算法和算法导论并不一样)入门例子:🔗 [深入理解快速排序(quciksort) - 知乎] https://zhuanlan.zhihu.com/p/63202860
但是上面的链接配图的步骤有点少,需要自己用一个更长的数组进行演算,加深印象。
参考算法导论写的代码:
def quicksort(A, l, r):
if l < r:
middle = partition(A, l, r)
quicksort(A, l, middle - 1)
quicksort(A, middle + 1, r)
return A
def partition(A, l, r):
base = A[r]
i = l - 1
j = l
while j < r:
if A[j] < base:
A[i + 1], A[j] = A[j], A[i + 1]
i += 1
j += 1
else:
j += 1
A[i + 1], A[j] = A[j], A[i + 1]
return i + 1
if __name__ == '__main__':
A = [2, 8, 7, 1, 3, 5, 6, 4]
print(quicksort(A, 0, len(A) - 1))
结果:
[1, 2, 3, 4, 5, 6, 7, 8]● Randomized quicksort
简单的说就是在quicksort算法里,把原本的【固定选择A[r]作为pivot】修改为【随机挑选A[i]作为pivot, i 为随机数】。这样做能够让worst case time complexity从原来的[mathjax]O(n^2)[/mathjax]变为[mathjax]O(n\log(n))[/mathjax].
即:
| Worst case | Best case | Average | |
| quicksort | [mathjax]O(n^2)[/mathjax] | [mathjax]O(n\log(n))[/mathjax] | [mathjax]O(n\log(n))[/mathjax] |
| randomized quicksort | [mathjax]O(n\log(n))[/mathjax] | [mathjax]O(n\log(n))[/mathjax] | [mathjax]O(n\log(n))[/mathjax] |
参考资料:
🔗 [Quicksort - Wikipedia] https://en.wikipedia.org/wiki/Quicksort#Analysis_of_randomized_quicksort
解释了为什么是[mathjax]O(n\log(n))[/mathjax]: 🔗 [algorithm analysis - Why does Randomized Quicksort have O(n log n) worst-case runtime cost - Computer Science Stack Exchange] https://cs.stackexchange.com/questions/35994/why-does-randomized-quicksort-have-on-log-n-worst-case-runtime-cost
用更容易理解的表达方式讲述了为什么是[mathjax]O(n\log(n))[/mathjax],同时附带了quicksort+randomized quicksort+代码:🔗 [算法导论(一):快速排序与随机化快排_Hamster-CSDN博客_随机快速排序] https://blog.csdn.net/haelang/article/details/44496387
验证代码:
import random
import time
import matplotlib.pyplot as plt
import sys
sys.setrecursionlimit(10000000)
def quicksort(A, l, r):
if l < r:
middle = partition(A, l, r)
quicksort(A, l, middle - 1)
quicksort(A, middle + 1, r)
def partition(A, l, r):
base = A[r]
i = l - 1
j = l
while j < r:
if A[j] < base:
A[i + 1], A[j] = A[j], A[i + 1]
i += 1
j += 1
else:
j += 1
A[i + 1], A[j] = A[j], A[i + 1]
return i + 1
def r_quicksort(A, l, r):
if l < r:
middle = r_partition(A, l, r)
r_quicksort(A, l, middle - 1)
r_quicksort(A, middle + 1, r)
def r_partition(A, l, r):
base = A[random.randint(l, r)]
i = l - 1
j = l
while j < r:
if A[j] < base:
A[i + 1], A[j] = A[j], A[i + 1]
i += 1
j += 1
else:
j += 1
A[i + 1], A[j] = A[j], A[i + 1]
return i + 1
def run(r_command):
quicksort_t = []
r_quicksort_t = []
for i in range(10, 1000, 1):
A = []
for j in range(0, i):
if r_command == 1:
A.append(random.randint(0, i))
else:
A.append(j)
start = time.time()
quicksort(A, 0, len(A) - 1)
quicksort_t.append(time.time() - start)
A = []
for j in range(0, i):
A.append(j)
start = time.time()
r_quicksort(A, 0, len(A) - 1)
r_quicksort_t.append(time.time() - start)
plt.figure()
axis = [i for i in range(10, 1000, 1)]
plt.scatter(axis, quicksort_t, label='quicksort')
plt.scatter(axis, r_quicksort_t, label='randomized quicksort')
plt.legend(loc='upper left')
if r_command == 1:
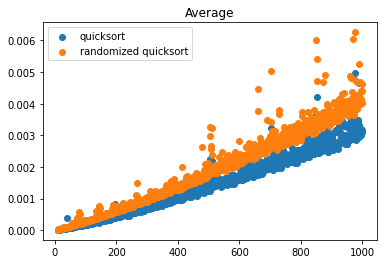
plt.title('Average')
else:
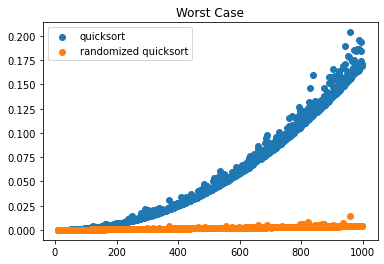
plt.title('Worst Case')
plt.show()
if __name__ == '__main__':
run(0)
run(1)
结果:
python 对象与递归
● 例子 (可以参考【python ++i和i++】):
def fun1(A):
A[-1] = 999
fun2(A)
print(A)
def fun2(A):
A[-2] = 888
A.append(1000)
A = A[:len(A) // 2]
if __name__ == '__main__':
A = [1, 2, 3, 4]
fun1(A)
结果:
[1, 2, 888, 999, 1000]对上面的程序进行一点修改:
def fun1(A):
A[-1] = 999
A = fun2(A)
print(A)
def fun2(A):
A[-2] = 888
A.append(1000)
A = A[:len(A) // 2]
return A
if __name__ == '__main__':
A = [1, 2, 3, 4]
fun1(A)
print(A)
运行结果:
[1, 2]
[1, 2, 888, 999, 1000]所以,本文之前的quicksort代码也可以这样写(区别在第6, 25, 26 行):
def quicksort(A, l, r):
if l < r:
middle = partition(A, l, r)
quicksort(A, l, middle - 1)
quicksort(A, middle + 1, r)
def partition(A, l, r):
base = A[r]
i = l - 1
j = l
while j < r:
if A[j] < base:
A[i + 1], A[j] = A[j], A[i + 1]
i += 1
j += 1
else:
j += 1
A[i + 1], A[j] = A[j], A[i + 1]
return i + 1
if __name__ == '__main__':
A = [2, 8, 7, 1, 3, 5, 6, 4]
quicksort(A, 0, len(A) - 1)
print(A)
python 堆排序/heap sort(继续)
继续之前的内容:🔗 [2021-10-15 - Truxton's blog] https://truxton2blog.com/2021-10-15/
(从之前的内容里直接拿)heap sort using max heap代码如下:
❗注意!这段代码没有做到就地排序,使用了额外空间,这是对max heap性质不熟练导致的。事实上,整个程序都有一些问题:max_heapify()的功能并不完整。
import random
def max_heapify(arr, i):
left = 2 * i + 1
right = 2 * i + 2
if left < len(arr) and arr[left] > arr[i]:
largest = left
else:
largest = i
if right < len(arr) and arr[right] > arr[largest]:
largest = right
if largest != i:
temp = arr[largest]
arr[largest] = arr[i]
arr[i] = temp
max_heapify(arr, largest)
else:
return arr
def build_max_heap(arr):
for i in range(len(arr) // 2 - 1, -1, -1):
max_heapify(arr, i)
return arr
def heap_sort(arr):
arr = build_max_heap(arr)
sorted = []
for i in range(len(arr) - 1, -1, -1):
temp = arr[i]
arr[i] = arr[0]
arr[0] = temp
sorted = [arr.pop()] + sorted
max_heapify(arr, 0)
return sorted
if __name__ == '__main__':
A = []
for i in range(0, 15):
A.append(random.randint(0, 50))
print(A)
C = heap_sort(A)
print(C)
● 有关写法:
注意上面代码的第35行,我平时非常习惯于使用 A.append(a) ,而现在需要使用 sorted = [arr.pop()] + sorted ,这段代码无法让我很好的回忆起“从一个最大堆导出排序数组”的细节。(因为上面的代码写的有问题)
在查找相关资料的时候发现了一些补充知识:🔗 [Python concatenation vs append speed on lists - Stack Overflow] https://stackoverflow.com/questions/25216962/python-concatenation-vs-append-speed-on-lists , 这段内容可以和【🔗 [2021-10-18 - Truxton's blog] https://truxton2blog.com/2021-10-18/ -> python 对象与递归】, 【🔗 [2021-10-15 - Truxton's blog] https://truxton2blog.com/2021-10-15/ -> python 初始化数组】相结合理解。
● 修改上面的heap sort using max heap(输入数据和中文算法导论p78一样,便于调试):
def max_heapify(arr, m, i):
# arr: input array;
# n: max index of arr (! important);
# i: build max heap starting from node i(index)
# does not need to return anything
largest = i
left = i * 2 + 1
right = i * 2 + 2
# find largest in : root, left, right
# important: check if left <= m (left node exists in THE CURRENT SCOPE max index m)
if left <= m and arr[i] < arr[left]:
largest = left
# important: check if right <= m (left node exists in THE CURRENT SCOPE max index m)
if right <= m and arr[largest] < arr[right]:
largest = right
if largest != i:
arr[largest], arr[i] = arr[i], arr[largest]
max_heapify(arr, m, largest)
def heap_sort(A):
# init a max heap
for i in range(len(A) // 2 - 1, -1, -1):
max_heapify(A, len(A) - 1, i)
for j in range(len(A) - 1, -1, -1):
# swap root and last node
A[0], A[j] = A[j], A[0]
max_heapify(A, j - 1, 0)
if __name__ == '__main__':
A = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
heap_sort(A)
print(A)
结果:
[1, 2, 3, 4, 7, 8, 9, 10, 14, 16]最小堆/min heap
● 类比上面的max heap - heap sort,现在使用最小堆来对一个数组从大到小排序:
def min_heap(A, m, i):
minimum = i
left = i * 2 + 1
right = i * 2 + 2
if left <= m and A[minimum] > A[left]:
minimum = left
if right <= m and A[minimum] > A[right]:
minimum = right
if minimum != i:
A[minimum], A[i] = A[i], A[minimum]
min_heap(A, m, minimum)
def heap_sort(A):
for i in range(len(A) // 2 - 1, -1, -1):
min_heap(A, len(A) - 1, i)
for j in range(len(A) - 1, -1, -1):
A[0], A[j] = A[j], A[0]
min_heap(A, j - 1, 0)
if __name__ == '__main__':
A = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
heap_sort(A)
print(A)
结果:
[16, 14, 10, 9, 8, 7, 4, 3, 2, 1]● 修改为priority queue
def min_heap(A, m, i):
minimum = i
left = i * 2 + 1
right = i * 2 + 2
if left <= m and A[minimum] > A[left]:
minimum = left
if right <= m and A[minimum] > A[right]:
minimum = right
if minimum != i:
A[minimum], A[i] = A[i], A[minimum]
min_heap(A, m, minimum)
def build_heap(A):
for i in range(len(A) // 2 - 1, -1, -1):
min_heap(A, len(A) - 1, i)
def pqueue_pop(A):
A[0], A[-1] = A[-1], A[0]
pop = A[-1]
# 这里可能还有改进空间,也许可以不创建新对象
B = A[:-1]
min_heap(B, len(B) - 1, 0)
return B, pop
if __name__ == '__main__':
A = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
build_heap(A)
while len(A) > 0:
A, pop = pqueue_pop(A)
print(pop, end=' ')
结果:
1 2 3 4 7 8 9 10 14 16