Audio Thumbnailing

Related: 该笔记可能存在后续补充内容，或在以前的笔记里被提及：

2022-03-29

为什么需要audio thumbnailing

通俗的说，audio thumbnailing相当于音乐作品的“概括性描述”，能够显示出音乐作品中最具代表性的片段。[1]

一个最直观的作用：听众可以通过audio thumbnailing快速了解一首歌最具代表性的旋律，然后决定要不要继续听完整作品；audio thumbnailing对音乐库的快速人工识别、检索也有很大帮助。[1]

比如我们(使用某个工具)对（希夫的）english suite no.5 prelude进行分析，获得了如下audio thumbnailing：

由于存在ssm后期处理难度、转调等诸多因素，本文在后续的audio thumbnailing 生成代码里并不会使用这首乐曲，而会使用[fundamental]书中的[Hungarian Dance No. 5]。

(希夫的)english suite no.5 prelude，未经后续处理的原始ssm大概就长这个样子：

最原始的audio thumbnailing生成原则

首先我们需要获得音频对应的ssm数据

[fundamental...]一书里，对thumbnailing segment path的选取规则进行了如下解释：我们需要用2个基本标准来逐步优化我们的segments选择：

1，给定一个segment，它和其他segments的相似度/关系 如何？

2，假定我们已经选好了一组segments，它们和整首音乐作品的关联如何？（覆盖率）

判断标准

好吧，既然audio thumbnailing截取是从ssm起步的，我们首先会知道：ssm矩阵对角线上的所有数值均为1，然后矩阵里的任意数值都必须小于或等于1。（这不是废话么，都是用欧氏距离/余弦相似度算出来的）

所以我们有了一个看上去像是废话的基本判断标准：我们必须先计算出一个合格的ssm矩阵，然后才能进行下一步计算。这里常常布满坑洞：在[funda]一书里，作者首先重复了ssm的几个基本数学性质，然后就直接开始进行audio thumbnailing的计算了。事实上，要较为良好地复现出书中的算法，需要对一个基础的ssm矩阵进行一些变换和修改，然后才能继续下一步。

path / segment / block

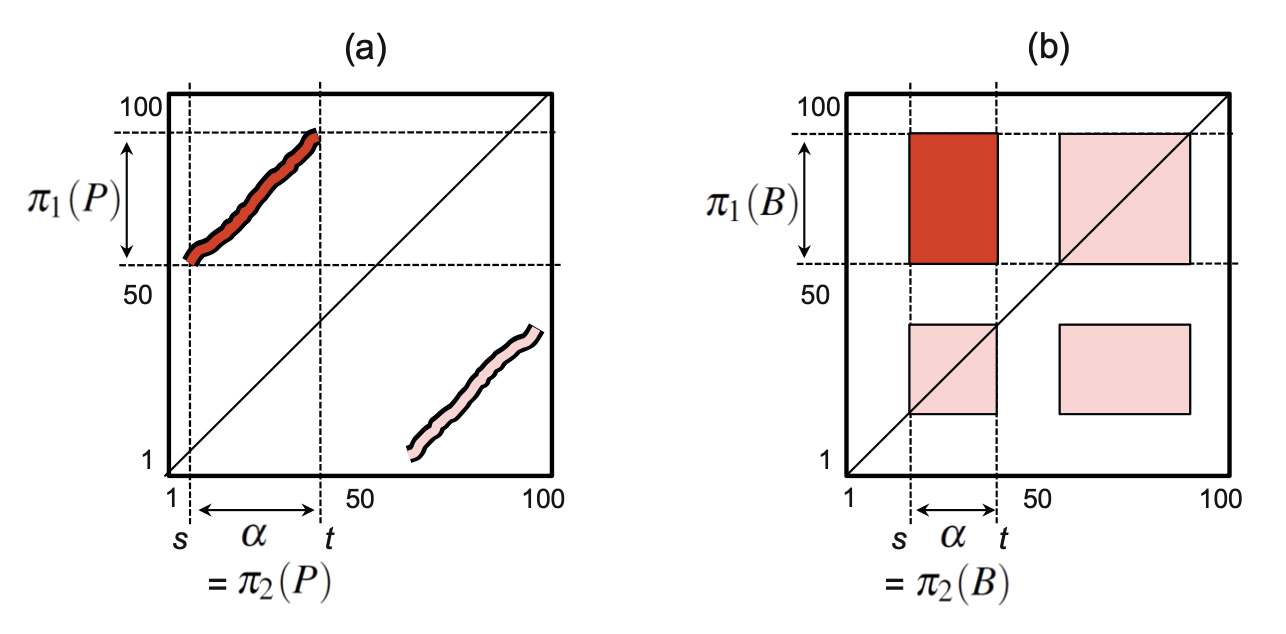
path：如左图所示，“红色的线条”

[mathjax]\pi _{1}( P) , \pi _{2}( P)[/mathjax]：path在坐标轴上的投影。

induced segment：[mathjax]\pi _{1}( P)[/mathjax]

block：如右图所示，“红色的区块”

path score：path所有点的数值的求和：[mathjax]\displaystyle \sum ^{L}_{l=1} S( n_{l} ,m_{l})[/mathjax]。显然，对ssm而言，矩阵对角线拥有最高path score。

block score：block所有点的数值的求和：[mathjax]\displaystyle \sum _{( n.m) \in B} S( n_{l} ,m_{l})[/mathjax]

path-similar / block-similar：已知[mathjax]\pi _{1}( P)=\alpha_{1}, \pi _{2}( P)=\alpha_{2}[/mathjax]，如果P（path）拥有较高path score，那么segment [mathjax]\alpha_{1}[/mathjax]和segment [mathjax]\alpha_{2}[/mathjax]可以认为是path-similar。block-similar同理。

path family / Induced segment family

path family是一系列paths的集合，同一个path family中的所有paths都需要满足它们来自同一个segment [mathjax]\pi_{2}P[/mathjax] 。

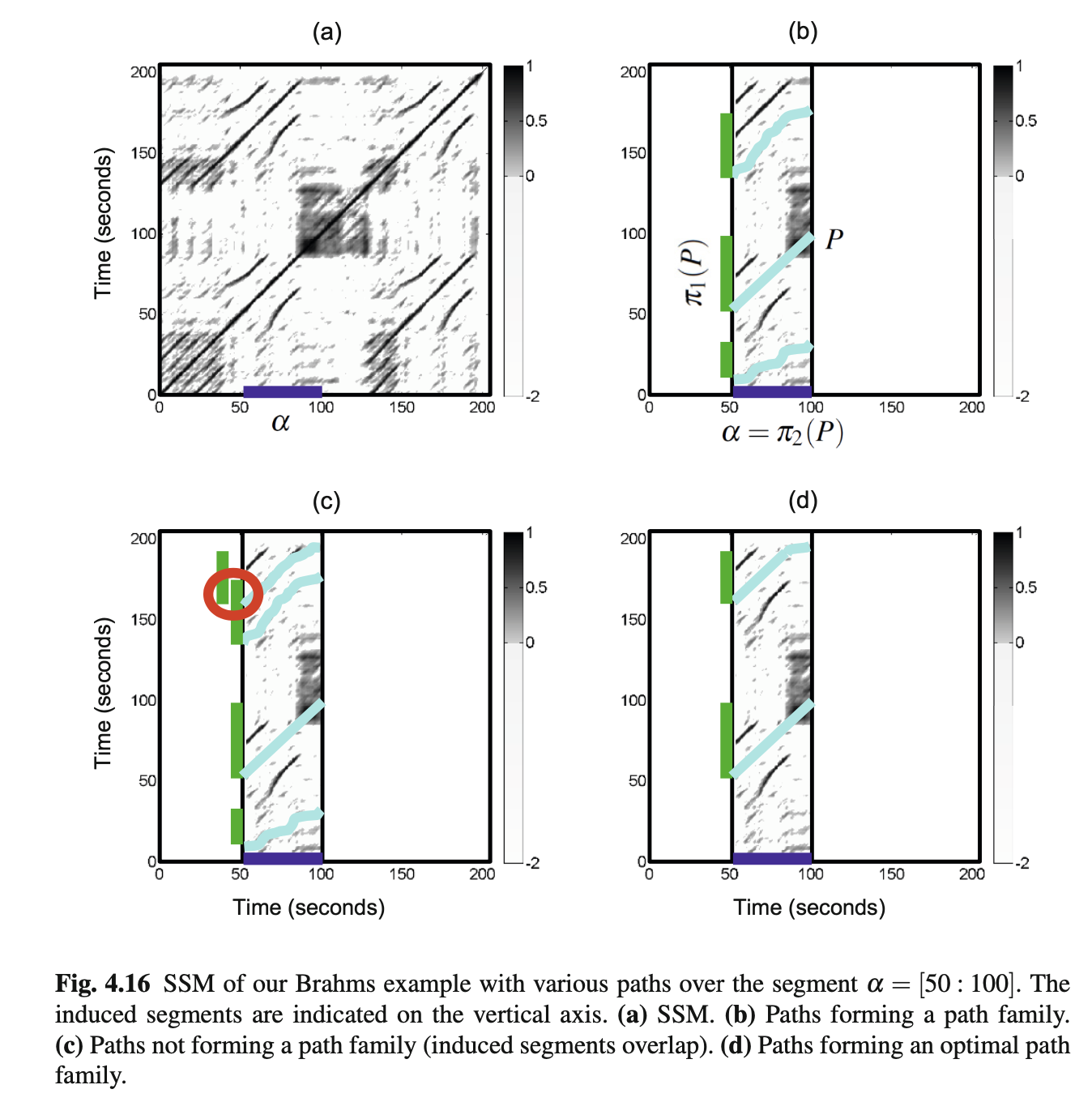
从图中可以看出，path family需要满足的一个最重要条件，就是induced segments不能出现任何重叠（overlapping）；在满足这个条件以后，就可以从多个path families里面找到分数最高的path family，作为optimal path family。

到目前为止，可以简单描述audio thumbnailing步骤：

1. 首先确定一个segment [mathjax]\alpha[/mathjax]，接下来的所有计算都要以它为基准；

2. 以这个segment为基准，可以生成很多induced segments；

3. 由于存在non-overlapping规则，事实上能够加入同一个path family的segments不会很多，所以最终一般会变成这个样子：有非常非常多的path families，每个path family里面有若干paths（一般都是个位数）；这些同一个path family下的paths进行分数权重累加，得到path family score。

4. 最终从path families里面找到sum score最高的path family。

Induced Segment family同理，由path family投影induced segments得到的集合，“图中绿色的线条代表了induced segment family投影”。

关键步骤：DTW

为什么使用一个修改版的DTW算法？因为某些教材是这么做的。此外，还有很多其他论文使用的算法并不是DTW，但我们可以先从DTW开始：

常规的DTW（Leetcode Easy DP）

就像leetcode上面常见的dynamic programming题一样。

一个DTW算法的前置DP题：https://leetcode.com/problems/unique-paths/

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        dp = [[1 for _ in range(n)] for _ in range(m)]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[m - 1][n - 1]


if __name__ == '__main__':
    print(Solution().uniquePaths(3, 7))

一个更加接近DTW的题：https://leetcode.com/problems/minimum-path-sum/

这道题距离[fundamental]一书里的最基础DTW示范还缺少两个条件：

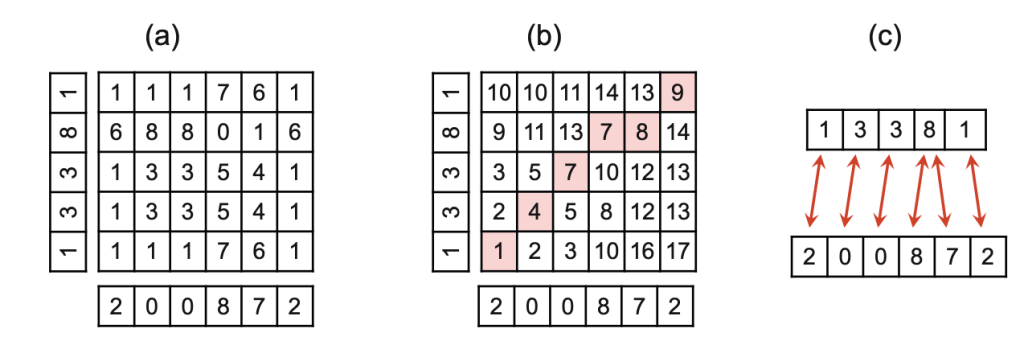
1，允许step(1, 1)，“向对角线方向走一格”。

2，不仅要得到minimum score，还要得到DTW path。

把这两个条件补上以后就得到了一个最基础的DTW（暂时没有使用numpy）

from typing import List


class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        grid_mincost = grid.copy()
        m = len(grid)
        n = len(grid[0])
        for i in range(0, m):
            for j in range(0, n):
                if i == 0 and j == 0:
                    grid_mincost[i][j] = grid_mincost[i][j]
                elif i - 1 < 0:
                    grid_mincost[i][j] = grid_mincost[i][j - 1] + grid[i][j]
                elif j - 1 < 0:
                    grid_mincost[i][j] = grid_mincost[i - 1][j] + grid[i][j]
                else:
                    grid_mincost[i][j] = min(grid_mincost[i - 1][j], grid_mincost[i][j - 1],
                                             grid_mincost[i - 1][j - 1]) + grid[i][j]

        # backtracking
        dtw_path = [[m - 1, n - 1]]
        path_i = m - 1
        path_j = n - 1
        while (True):
            if path_i == 0 and path_j == 0:
                break
            elif path_i == 0:
                dtw_path.append([path_i, path_j - 1])
                path_j -= 1
            elif path_j == 0:
                dtw_path.append([path_i - 1, path_j])
                path_i -= 1
            else:
                a = grid_mincost[path_i - 1][path_j]
                b = grid_mincost[path_i][path_j - 1]
                c = grid_mincost[path_i - 1][path_j - 1]
                if a <= b and a <= c:
                    dtw_path.append([path_i - 1, path_j])
                    path_i -= 1
                elif b <= a and b <= c:
                    dtw_path.append([path_i, path_j - 1])
                    path_j -= 1
                else:
                    dtw_path.append([path_i - 1, path_j - 1])
                    path_i -= 1
                    path_j -= 1

        print(dtw_path)
        return grid_mincost[m - 1][n - 1]


if __name__ == '__main__':
    print(Solution().minPathSum(
        grid=[[1, 1, 1, 7, 6, 1], [1, 3, 3, 5, 4, 1], [1, 3, 3, 5, 4, 1], [6, 8, 8, 0, 1, 6], [1, 1, 1, 7, 6, 1]]))
    
    

修改过的DTW和SSM

[fundamen...]这本书里，对DTW和DTW计算过程中使用得SSM都进行了一定的修改。

首先是SSM，为了保证后续的修改版DTW算法能够继续，我们需要在矩阵中引入negative score。“原版”的ssm矩阵应当拥有一个[0, 1]的值域限制，这里对它进行了一点小修改：

对所有ssm里的数值进行一次阈值判断：高于某个阈值的全部scaling到[0, 1]区间；低于这个值域的全部设置为0，或者全部设置为某个负数。这就导致了修改过的ssm矩阵中出现负数。[ref]

补充：其他参考资料

除了《Fundamentals of ...》，还有其他参考audio thumbnailing的资料/代码实现：

（网页中搜索thumbnailing即可）🔗 [pyAudioAnalysis/audioSegmentation.py at master · tyiannak/pyAudioAnalysis · GitHub] https://github.com/tyiannak/pyAudioAnalysis/blob/master/pyAudioAnalysis/audioSegmentation.py