李航《统计学系方法》第8章：提升方法 - 入门学习笔记

by   Last Modified in 2023-12-04Categories Home ❯ Garbage
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

本笔记对应的PDF

原本的目标是学会gradient boosting decision tree/梯度提升决策树/GBDT，实际上写完一个简单的python Adaboost demo以后就没继续学了。最初的学习原因应该是看到某篇论文里面用了GBDT，所以想入门学习一下boosting大概是什么东西（以前总是跳过这部分）。

不同PDF阅读器的显示效果不同，如果渲染PDF出现偏差，请尝试其他PDF阅读器

一些零散的学习笔记

什么是boosting

强可学习 strongly learnable

弱可学习 weakly learnable，有一个1/2作为界限进行判断，这个1/2以后会用到

概率近似正确 probably approximately correct/PAC

弱学习算法->提升->强学习算法，这个过程就是boosting

Adaboost学习笔记和代码

P157

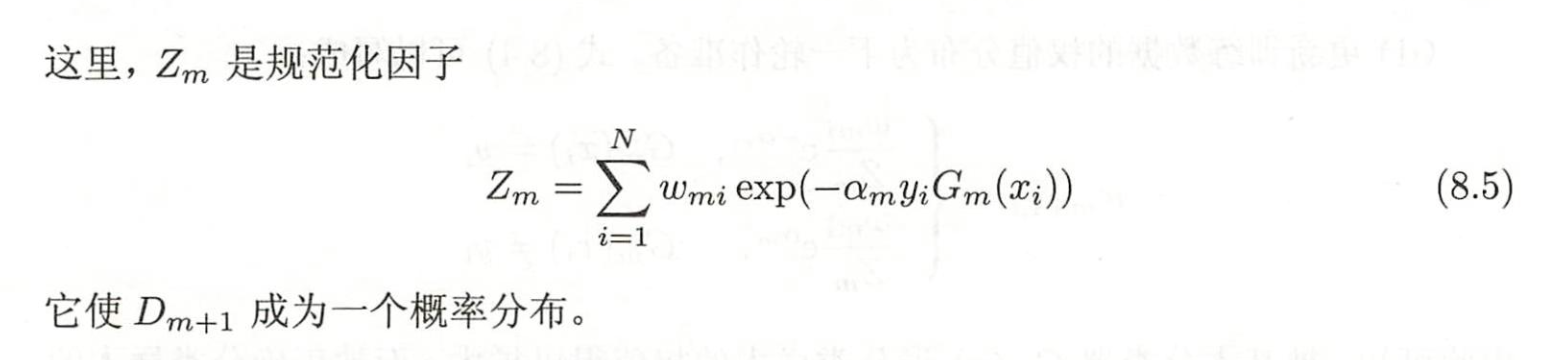
D_m+1成为概率分布是可以推导出来的：每一轮D的所有权重（w）的和都为1. （大概长这样）

sign()符号：p35

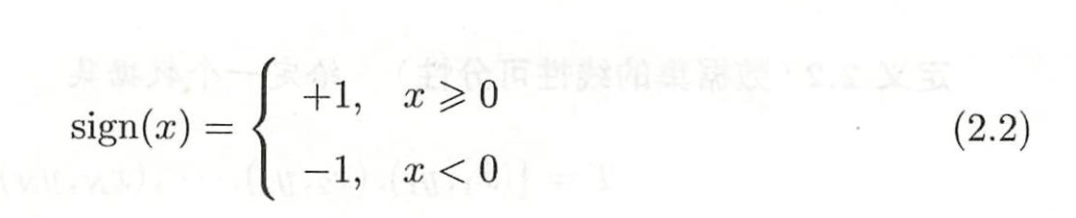
adaboost的终止：能100%正确当然最好，否则差不多得了

然后开始看李航p159的例题：

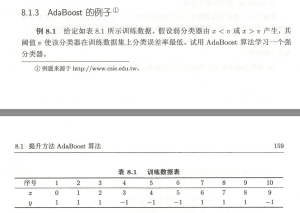
手算令人烦躁，而且这部分内容总是理解不透：

也就是题目解答的这一部分（为什么v=8.5的时候误差率最低，我怎么手算不出相同的结果）

到底该怎么加权后训练？具体的过程是怎么样的？为了确认我理解的东西没有问题，只能手写程序看看能不能和书上的结果对上了：

临时跑去写了个python，极其丑陋，写这个代码的目的仅仅是不想手算书上的例题：

import numpy as np

x = [i for i in range(0, 10)]  # 0~9
y = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]

if len(x) != len(y):
    print('err')
    exit(1)

N = len(x)

d = [[1 / N] * N]
alpha = []
classifier_lst = []


def sign(input):
    if input >= 0:
        return 1
    else:
        return -1


class BinaryClassifier:
    border = None
    inverse = None
    weight = None

    def __init__(self, border, inverse, weight):
        self.border = border
        self.inverse = inverse
        self.weight = weight

    def output(self, x):
        if (self.inverse == True and x > self.border) or (self.inverse == False and x < self.border):
            return 1
        else:
            return -1


def check_classifier_lst_err_count():
    count = 0
    for i in range(0, N):
        sum = 0
        for BinaryClassifier in classifier_lst:
            sum += BinaryClassifier.output(i) * BinaryClassifier.weight
        if sign(sum) != y[i]:
            count += 1

    return count


def weak_optimal_finder(round, inverse):
    best_x = -1
    best_x_err_weight = 1
    best_x_err_index = []
    for try_x in np.arange(0.5, N + 0.5, 1):
        # print(try_x)
        weighted_err = 0
        err_x_index = []
        for right_x in range(int(try_x + 1), N):
            # should be -1, if not...
            if (y[right_x] != -1 and (inverse == False)) or (y[right_x] != 1 and (inverse == True)):
                weighted_err += 1 * d[round - 1][right_x]
                err_x_index.append(right_x)
        for left_x in range(0, int(try_x) + 1):
            # should be 1, if not...
            if (y[left_x] != 1 and (inverse == False)) or (y[left_x] != -1 and (inverse == True)):
                weighted_err += 1 * d[round - 1][left_x]
                err_x_index.append(left_x)
        if weighted_err < best_x_err_weight:
            best_x = try_x
            best_x_err_weight = weighted_err
            best_x_err_index = err_x_index  # 不需要deepcopy
    return best_x, best_x_err_weight, best_x_err_index


# print(best_x, best_x_err)
for m in range(1, 99):
    (best_x_no_inverse, best_x_err_weight_no_inverse, best_x_err_index_no_inverse) = weak_optimal_finder(round=m,
                                                                                                         inverse=False)
    (best_x_inverse, best_x_err_weight_inverse, best_x_err_index_inverse) = weak_optimal_finder(round=m, inverse=True)

    inverse = None
    if best_x_err_weight_no_inverse > best_x_err_weight_inverse:
        # 需要反转
        best_x = best_x_inverse
        best_x_err_index = best_x_err_index_inverse
        inverse = True
    else:
        # 不需要反转
        best_x = best_x_no_inverse
        best_x_err_index = best_x_err_index_no_inverse
        inverse = False

    print(best_x)

    err_rate = 0
    for index in best_x_err_index:
        err_rate += d[m - 1][index]
    print(err_rate)
    alpha.append(0.5 * np.log((1 - err_rate) / err_rate))
    print(alpha)

    classifier_lst.append(BinaryClassifier(best_x, inverse, alpha[-1]))
    print('总分类器错误个数：' + str(check_classifier_lst_err_count()))

    if check_classifier_lst_err_count() == 0:
        print('Done')
        exit(1)

    # print(alpha)
    z_m_temp = 0
    updated_w = []
    for i in range(0, N):
        if i > best_x:
            z_m_temp += d[m - 1][i] * np.exp(-alpha[m - 1] * y[i] * (-1))
        else:
            z_m_temp += d[m - 1][i] * np.exp(-alpha[m - 1] * y[i] * (1))
    for i in range(0, N):
        if i > best_x:
            updated_w.append(d[m - 1][i] / z_m_temp * np.exp(-alpha[m - 1] * y[i] * (-1)))
        else:
            updated_w.append(d[m - 1][i] / z_m_temp * np.exp(-alpha[m - 1] * y[i] * (1)))
    d.append(updated_w)

    print('--------------------')

运行结果：

2.5
0.30000000000000004
[0.4236489301936017]
总分类器错误个数：3
--------------------
8.5
0.21428571428571427
[0.4236489301936017, 0.6496414920651304]
总分类器错误个数：3
--------------------
5.5
0.18181818181818185
[0.4236489301936017, 0.6496414920651304, 0.752038698388137]
总分类器错误个数：0
Done

除了令人作呕的垃圾逻辑以外，上面的代码还有一个别的问题：

如果把那个退出adaboost迭代的代码exit(1)去掉，让adaboost一直跑下去，会发现结果变成了：

令人疑惑的输出结果
2.5
0.30000000000000004
[0.4236489301936017]
总分类器错误个数：3
--------------------
8.5
0.21428571428571427
[0.4236489301936017, 0.6496414920651304]
总分类器错误个数：3
--------------------
5.5
0.18181818181818185
[0.4236489301936017, 0.6496414920651304, 0.752038698388137]
总分类器错误个数：0
Done
--------------------
5.5
0.04705882352941177
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274]
总分类器错误个数：4
--------------------
5.5
0.002432720085145204
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548]
总分类器错误个数：4
--------------------
5.5
5.94699135319073e-06
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096]
总分类器错误个数：4
--------------------
5.5
3.536712680841831e-11
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192]
总分类器错误个数：4
--------------------
5.5
1.2508336587712184e-21
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383]
总分类器错误个数：4
--------------------
5.5
1.5645848419149923e-42
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383, 48.130476696840766]
总分类器错误个数：4
--------------------
5.5
2.447925727550162e-84
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383, 48.130476696840766, 96.26095339368153]
总分类器错误个数：4
--------------------
5.5
5.99234036760199e-168
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383, 48.130476696840766, 96.26095339368153, 192.52190678736306]
总分类器错误个数：4
--------------------
5.5
0.0
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383, 48.130476696840766, 96.26095339368153, 192.52190678736306, inf]
总分类器错误个数：4
--------------------
5.5
0.0
[0.4236489301936017, 0.6496414920651304, 0.752038698388137, 1.504077396776274, 3.008154793552548, 6.016309587105096, 12.032619174210192, 24.065238348420383, 48.130476696840766, 96.26095339368153, 192.52190678736306, inf, inf]
总分类器错误个数：4
--------------------
-1
0


（直到触发分母=0的错误）
ZeroDivisionError: division by zero in alpha.append(0.5 * np.log((1 - err_rate) / err_rate))

总之就是，从最优结果以后，总分类器就再也没有"错误个数=0"的效果了，而是“错误个数=4”，且会一直下去。

可能是这行代码导致的：

for try_x in np.arange(0.5, N + 0.5, 1):

这行代码主要是模仿书本上的例子，所有弱分类器的边界都是x.5，比如2.5, 5.5, 8.5

程序里也这样写未必是好的

不管了，程序能跑对就行，跑对以后的代码不关我事。

所以那个“加权后训练”的意思就是，训练的基准是“分类误差率”，而不是“分错了多少个”

总结一下写代码过程中遇到的细节，防止下次忘了：

  1. “分类误差率“要理解对，在计算“分类误差率”的时候使用的是简单的弱分类器，而不是sign()这个效果强的合体分类器
  2. 分类器sign()的分类效果负责决定什么时候adaboost停止
  3. 弱分类器的代码要写对写全，比如这个反转判断的陷阱
  4. 强分类器sign()像火车挂车厢一样，从车头开始往后一节一节挂车厢，而且挂好的车厢（弱分类器的权重系数）不会再变


 Last Modified in 2023-12-04 

Leave a Comment Anonymous comment is allowed / 允许匿名评论