This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
集成学习区分图
原文件是2025-06-27创建的.drawio
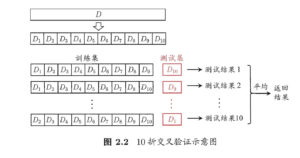
k-fold cross validation
k-fold cross validation/交叉验证
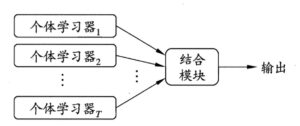
集成学习/ensemble learning
集成学习/ensemble learning
下面内容参考周志华机器学习P171-P172
周志华机器学习第8章就是【集成学习】，里面介绍了2种集成学习方法：boosting（以前学过，见下文）和bagging-随机森林.
下面这张图介绍了【集成学习的难点】，以及为什么需要boosting和bagging.
boosting和bootstrapping
boosting, bootstrapping
比较容易搞混的2个词语，实际上不是一个东西（bagging=bootstrapping=Bootstrap aggregating，而bagging和boosting同属于ensemble learning）. bootstrapping是一种采样方法，用来和交叉验证等采样方法进行比较；boosting是另一种集成学习方法.
或者见本笔记置顶的这张图辅助理解。
boosting见🔗 [李航《统计学系方法》第8章：提升方法 - 入门学习笔记 - Truxton's blog] https://truxton2blog.com/boosting-learning-lihang-statistical_learning_methods-chapter8/
bootstrapping以前应该没有写过类似笔记
理解bootstrapping的关键：[mathjax]m[/mathjax]既是原始数据集的样本个数，也是采集数据集的样本个数，还是单次抽样的次数。这就是为什么当[mathjax]m[/mathjax]趋于无穷大时仍然有36.8%的原始数据没有被采集到（因为此时原始数据集的样本个数[mathjax]m[/mathjax]也趋向于无穷大）
bagging
下面是另一种集成学习：bagging
random forest是bagging的一个拓展，random forest也属于bagging
先介绍bagging的来历（为什么集成学习需要bagging）
然后是bagging的实现方式：
(bagging) 简单来说就是重复T次bootstrapping抽样，每次抽出来的结果训练1个基学习器，最后就有了T个基学习器，这T个基学习器使用的训练数据（相互之间）有所重叠，但又不完全相同。
random forest在bagging的基础上额外增加的特性：每棵树的features也是随机分配的。
随机森林/Random Forest
随机森林/Random Forest
（学习阶段1）
随机森林是bagging的一个拓展
由于学随机森林的时候决策树没有完全搞懂，所以理解下面这句话的时候出现了困难（实际上并不影响随机森林的学习）：
我当时的疑惑主要是“这d个属性经过这个结点处理后，下一层还剩下多少属性“。所以跑去再次学习了一遍决策树：🔗 [2025-02-09 决策树 - Truxton's blog] https://truxton2blog.com/2025-02-09-decision-tree/ 见笔记末尾部分。
所以上面的问题解决了：（决策树）这d个属性经过这个结点处理后，下一层既有可能是d个属性，也有可能是d-1个属性，主要取决于这个结点选择的最有属性是连续变量还是离散变量（如果是离散变量，则又进一步取决于决策树的算法以及这个离散变量的特征数是多少）。
实际上学习随机森林并不需要上面的这些准备资料，直接看下面的图片即可（尤其是最后两句的解释）：
（学习阶段2）
但还是要注意，上面图片第二段的描述（有关随机选择的k集合）仅仅作用于一棵树；事实上，一个random forest = 多棵特殊的decision tree(s)，每棵树具有自己的抽样数据（来自bootstrapping）和自己的k个随机属性，最后这些决策树会聚在一起投票出一个最终结果（投票还分soft voting和hard voting，见本文稍后的内容）。
参见下面的gpt问答：
Q: in my understanding, random forest is just a special decision tree, for each layer, it has a special collection of features to choose the best. however, why it's ensemble learning?
A:
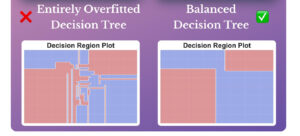
最后是单棵decision tree（使用全部变量训练）vs Random Forest:
Soft voting和hard voting
soft voting和hard voting
（属于ensemble learning的内容，也就是最后一步，当多个学习器各自得到自己的结果后，我们应该如何根据这些学习器的结果得出一个最终结论）
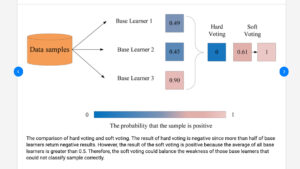
解释：<0.5的分类为0，>=0.5的分类为1
hard voting：2个学习器得到0，1个学习器得到1，投票：2>1，所以最终分类为0
soft voting：3个学习器的平均概率为0.61，0.61>0.5，所以最终分类为1
由随机森林得到的变量重要程度排名
（下面的内容来自gpt）
先假定这里指的都是普通的单决策变量树（特殊的多决策变量树暂时不考虑：🔗 [2025-02-09草稿（未发表） - Truxton's blog] https://truxton2blog.com/?p=16060&preview=true ）
每个节点决策一个变量，这个变量对于子节点的基尼不纯度的改善是可以计算的。把随机森林的每棵树的每个节点的变量都统计一遍，每个变量的“改善”进行累加，（正则化0～1以后）进行排名，就可以得到所有变量的重要程度的排名。
Gradient boosting
gradient boosting
基于决策树的ensemble learning algorithm
比较新，2001年的论文 Friedman, Jerome H. "Greedy function approximation: a gradient boosting machine." Annals of statistics (2001): 1189-1232.
用下面这张图理解：
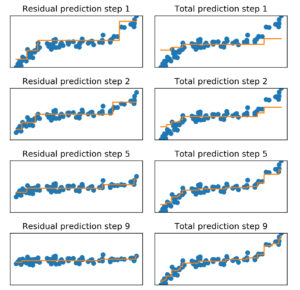
顺序是：从上往下一共4步，每一步左边是residual，右边是总体拟合效果。所以右下角是最终结果，也可以看到residual随着步骤推进变得越来越小，意味着gradient boosting正在逐渐拟合原有数据。
