This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
(long1, lat1), (long2, lat2)两点间的距离计算
之前一直用long, lat -> utm (x, y)的方法计算直线距离，但忽略了一个问题：utm可能跨区域。之前用到这个计算距离的场景都是小范围距离计算，但现在不能这么用了，现在肯定要用通用的标准方法。
标准算法是 Haversine Formula . 算法本身非常容易实现：
🔗 [engineering.purdue.edu/ece477/Archive/2008/Spring/S08-Grp03/nb/datasheets/haversine.pdf] https://engineering.purdue.edu/ece477/Archive/2008/Spring/S08-Grp03/nb/datasheets/haversine.pdf
所以自己就能写：
import math
# 注意返回的单位是km
# 注意传入lat和long的时候不要写反
# example: my_haversine(47.80844, -122.43159, 26.94168, -80.80621)
def my_haversine(lat1, long1, lat2, long2):
lat1, long1, lat2, long2 = map(math.radians, [lat1, long1, lat2, long2])
dlon = long2 - long1
dlat = lat2 - lat1
a = math.sin(dlat / 2) ** 2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2) ** 2
c = 2 * math.asin(min(1, math.sqrt(a)))
R = 6371.0088
d = R * c
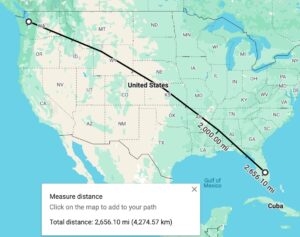
return d用google map的距离测算验证一组（粗略验证，因为google map不方便在测算距离的时候复制高精度经纬度）：
(47.80844, -122.43159)
到
(26.94168, -80.80621)我的函数计算结果：
google map的距离测算：
再导入一个haversine包：🔗 [mapado/haversine: Calculate the distance between 2 points on Earth] https://github.com/mapado/haversine
跑10000组随机经纬度进行结果对比：
import math
import random
import haversine
# 注意返回的单位是km
# 注意传入lat和long的时候不要写反
# example: my_haversine(47.80844, -122.43159, 26.94168, -80.80621)
def my_haversine(lat1, long1, lat2, long2):
lat1, long1, lat2, long2 = map(math.radians, [lat1, long1, lat2, long2])
dlon = long2 - long1
dlat = lat2 - lat1
a = math.sin(dlat / 2) ** 2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2) ** 2
c = 2 * math.asin(min(1, math.sqrt(a)))
R = 6371.0088
d = R * c
return d
for i in range(0, 10 ** 4):
rand_long1 = random.uniform(-180, 180)
rand_long2 = random.uniform(-180, 180)
rand_lat1 = random.uniform(-90, 90)
rand_lat2 = random.uniform(-90, 90)
my_haversine_dist = my_haversine(lat1=rand_lat1, long1=rand_long1, lat2=rand_lat2, long2=rand_long2)
standard_haversine_dist = haversine.haversine((rand_lat1, rand_long1), (rand_lat2, rand_long2))
if abs(my_haversine_dist - standard_haversine_dist) > 10 ** (-10):
print(f'not equal: {abs(my_haversine_dist - standard_haversine_dist)}')
exit(1)
print('pass')通过了10000组随机测试，所以认为上面自己写的 my_haversine 没有什么问题
(long1, lat1), (long2, lat2)连线中任意一点的坐标计算
两种不同的解释方法
假设有一个参数[mathjax]\alpha \in [0, 1][/mathjax]用来表示两点间连线的任意一点，求这个点的经纬度坐标（用long和lat表示）
这个“连线”有2种解释：（下面假设这两个点在地球上距离相当远，已经不能忽略球体曲面的影响了）
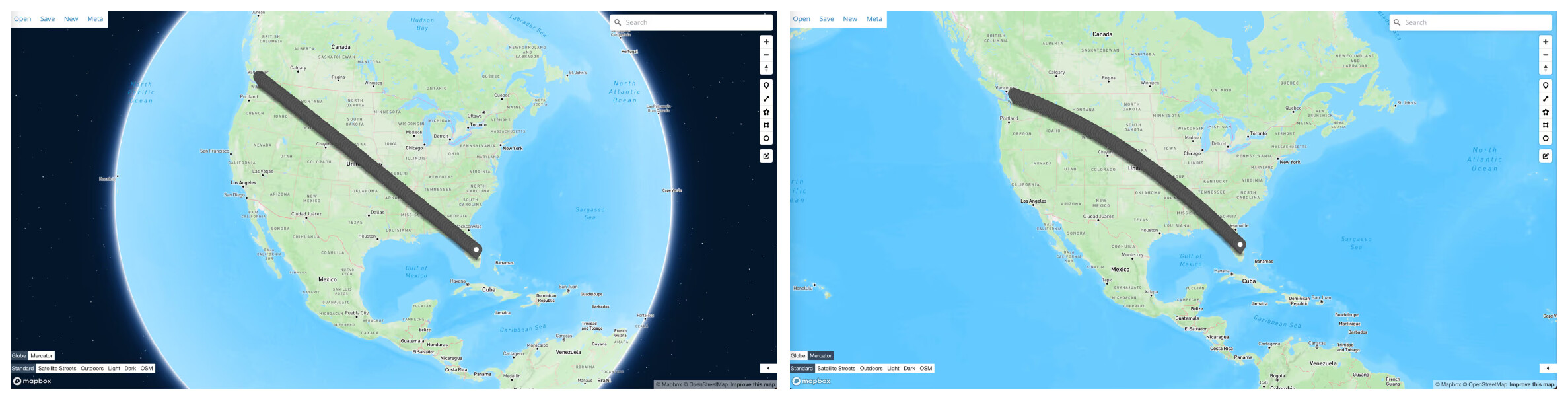
解释1：在球体地图上表现为曲线，在展开地图上表现为直线
（可视化网站是geojson.io，geojson文件：解释1的geojson）
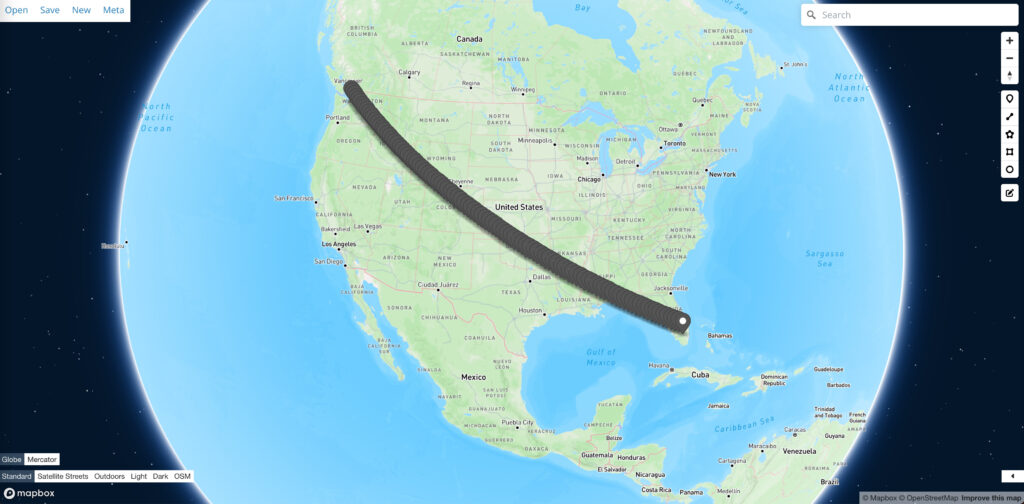
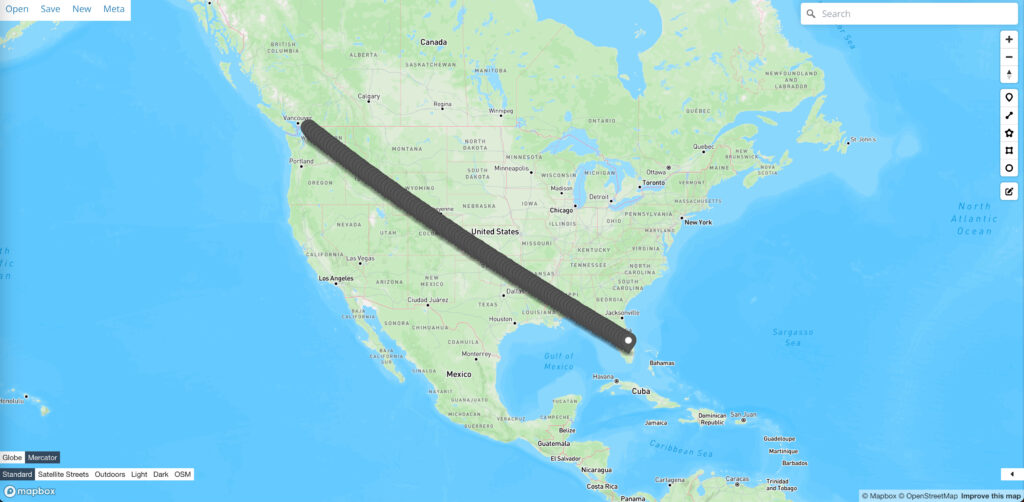
解释2：在球体地图上表现为直线，在展开地图上表现为曲线
（geojson文件：解释2的geojson）
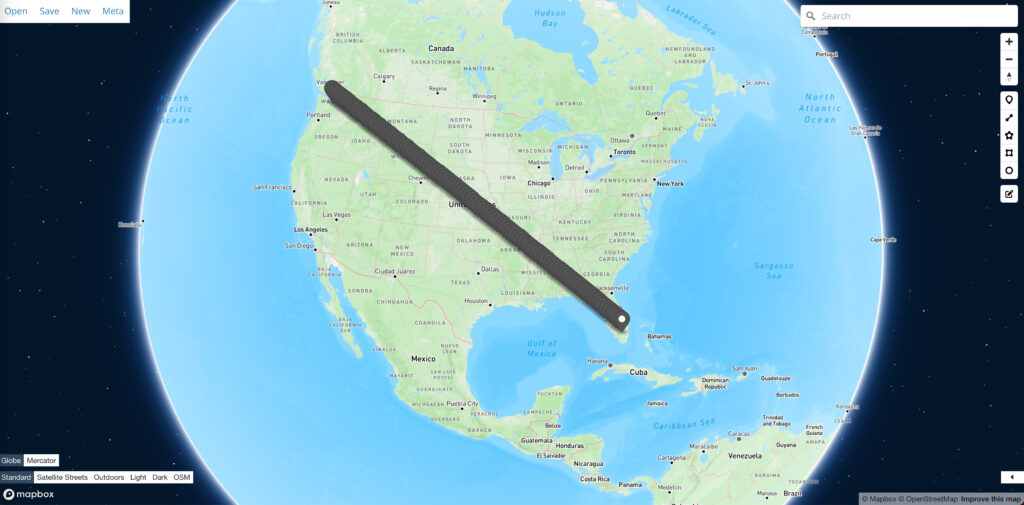
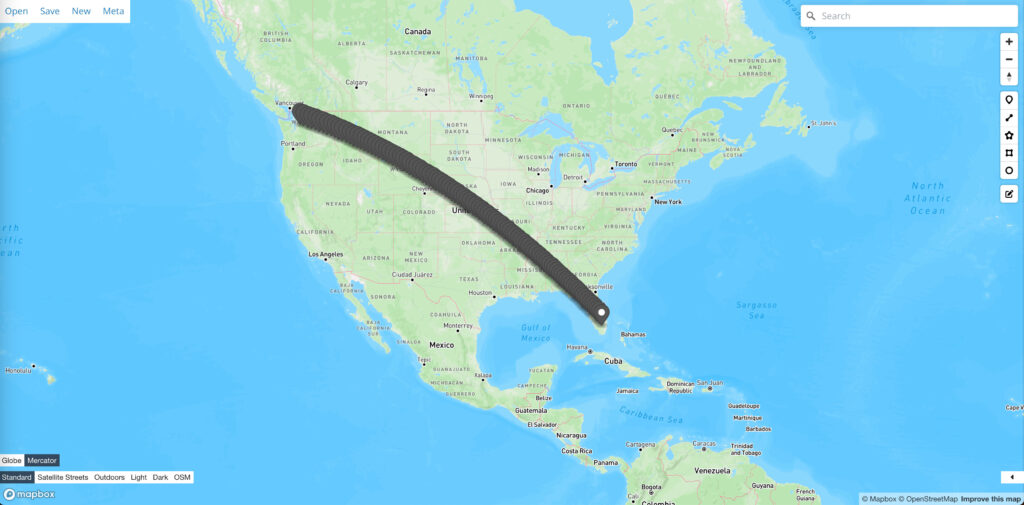
我也不知道哪一种才是GIS业界“默认”的，只能把这两种解释的代码都贴出来。
解释1（by straight-line distance）
解释1：在球体地图上表现为曲线，在展开地图上表现为直线
实现代码和原理非常非常简单。就是把经纬度的坐标直接当成平面直角坐标系里的(x, y)，然后用线性代数的向量计算就可以搞定。
如果调用 shapely 包里的 line.interpolate 计算，也会使用这种“简单易懂“的2D平面坐标系进行计算。
shapely:
def middle_shapely(alpha, long1, lat1, long2, lat2):
line = LineString([Point(long1, lat1), Point(long2, lat2)])
# Calculate the midpoint with alpha = 0.5
midpoint = line.interpolate(alpha, normalized=True)
# Display the midpoint's coordinates
return midpoint.x, midpoint.y # x is longitude, y is latitude自己写的：
def middle_my(alpha, long1, lat1, long2, lat2):
return long1 + (long2 - long1) * alpha, lat1 + (lat2 - lat1) * alpha对比代码：
from shapely.geometry import LineString, Point
import geojson
import numpy as np
import os
lat1, long1 = 47.85391930413978, -121.7528973290274
lat2, long2 = 26.382806911861756, -80.84341092679324
def middle_shapely(alpha, long1, lat1, long2, lat2):
line = LineString([Point(long1, lat1), Point(long2, lat2)])
# Calculate the midpoint with alpha = 0.5
midpoint = line.interpolate(alpha, normalized=True)
# Display the midpoint's coordinates
return midpoint.x, midpoint.y # x is longitude, y is latitude
def middle_my(alpha, long1, lat1, long2, lat2):
return long1 + (long2 - long1) * alpha, lat1 + (lat2 - lat1) * alpha
# shapely
points = [(x, y) for x, y in [middle_shapely(alpha, long1, lat1, long2, lat2) for alpha in np.linspace(0, 1, 101)]]
features = [geojson.Feature(geometry=geojson.Point((x, y))) for x, y in points]
feature_collection = geojson.FeatureCollection(features)
geojson_data = geojson.dumps(feature_collection, indent=2)
with open("points_shapely.geojson", "w") as file:
file.write(geojson_data)
# 自己写的
points = [(x, y) for x, y in [middle_my(alpha, long1, lat1, long2, lat2) for alpha in np.linspace(0, 1, 101)]]
features = [geojson.Feature(geometry=geojson.Point((x, y))) for x, y in points]
feature_collection = geojson.FeatureCollection(features)
geojson_data = geojson.dumps(feature_collection, indent=2)
with open("points_my.geojson", "w") as file:
file.write(geojson_data)
# 对比结果
os.system('diff ./points_shapely.geojson ./points_my.geojson')对比结果为：两个geojson文件完全一致。
解释2（by geodesic）
解释2：在球体地图上表现为直线，在展开地图上表现为曲线
这个就要复杂一些了，我让chatgpt给我写了个函数，结果看起来没问题，但具体坐标的数字和标准答案（假设pyproj给出的答案为标准答案）有点出入，所以下面的代码只放pyproj的了：
import pyproj
import geojson
import numpy as np
lat1, long1 = 47.85391930413978, -121.7528973290274
lat2, long2 = 26.382806911861756, -80.84341092679324
def middle_by_geodesic(alpha, long1, lat1, long2, lat2):
# Define the geodesic projection
geod = pyproj.Geod(ellps='WGS84')
# Get the azimuth and distance between the points
az12, az21, dist = geod.inv(long1, lat1, long2, lat2)
dist_alph = dist * alpha
# Find the point at alpha distance
lon3, lat3, _ = geod.fwd(long1, lat1, az12, dist_alph)
return lon3, lat3
points = [(x, y) for x, y in [middle_by_geodesic(alpha, long1, lat1, long2, lat2) for alpha in np.linspace(0, 1, 101)]]
features = [geojson.Feature(geometry=geojson.Point((x, y))) for x, y in points]
feature_collection = geojson.FeatureCollection(features)
geojson_data = geojson.dumps(feature_collection, indent=2)
with open("points_geodesic.geojson", "w") as file:
file.write(geojson_data)