This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.这篇笔记2023年10月就想写了，但实际上拖到2024-10-27才开始学
Table of Contents
学习
学习顺序：
先看了下lp and network flow的big-M方法：
但一直没找到我想要的“使用big-M打开局面“的那种题（也就是一开始无法直接使用tableau的题），直到example 4.10我才遇到一次：
但这道题的解法是什么THE SINGLE ARTIFICIAL VARIABLE TECHNIQUE，不是我想要的big-M.
换个教材。搜到了🔗 [personal.utdallas.edu/~scniu/OPRE-6201/documents/LP07-Big-M-Formulation.pdf] https://personal.utdallas.edu/~scniu/OPRE-6201/documents/LP07-Big-M-Formulation.pdf
pdf包含了100%我想要的内容：
- 给出了一道“不能直接tableau“的例题
- 逐步分析”应该如何应对“
- 讲解big-M方法
- 给出了例题的解题步骤（虽然没有完整步骤，但前几步是有的，已经足够了）
关键的讲解在前2页：
其中有个名词 candidate basic variable 在书上没找到解释，后来在这里找到了：🔗 [Initialization and Other Considerations] https://personal.utdallas.edu/~scniu/OPRE-6201/documents/LP5-Other_Considerations.html，解释为“a variable that has a coefficient of 1 and appears in that equation only”. 下面是一些例子：
所以读完这个PDF（以及跟着做了这个pdf自带的那道例题）以后就能做example 4.10了：
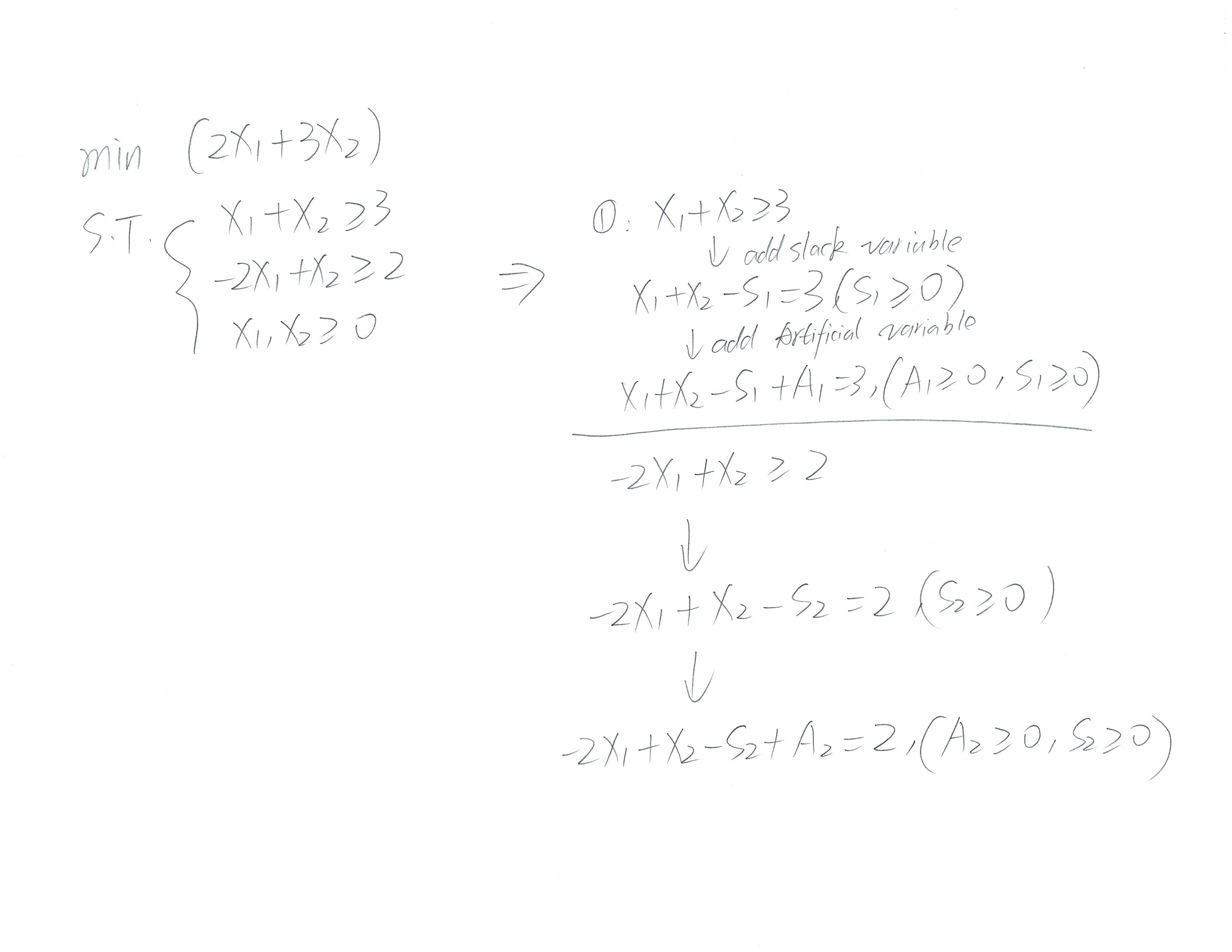
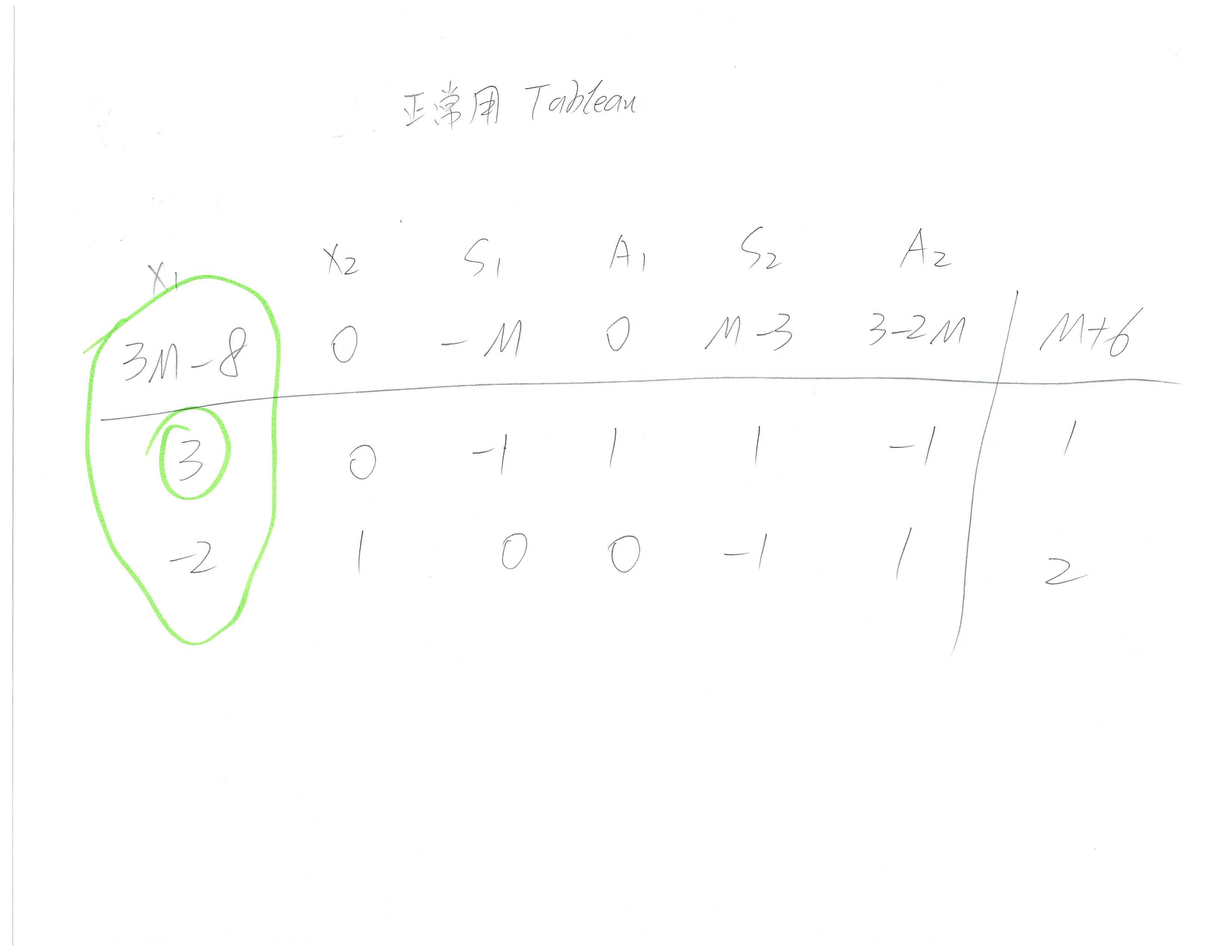
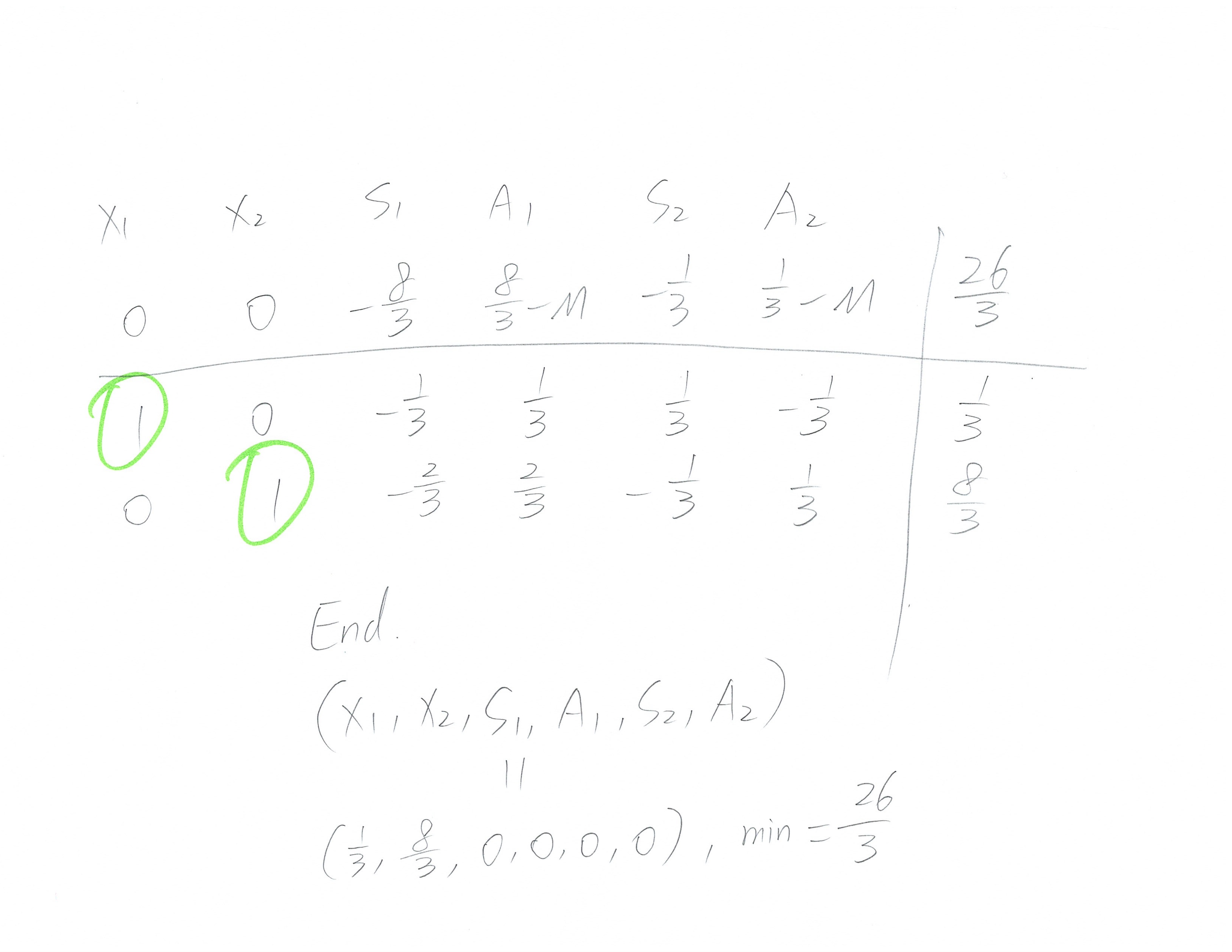
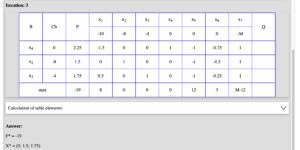
附上linprog.com的解答以便对照：
解决经典例题
例题来自🔗 [LP Tableau法 - Truxton's blog] https://truxton2blog.com/lp-tableau-method/的笔记开头部分
最后再看看这个例题：
特别注意，因为这里是max()类型的问题，所以不能直接照搬上面min()的解法，要用-M*Artificial_variable
完整过程如下：
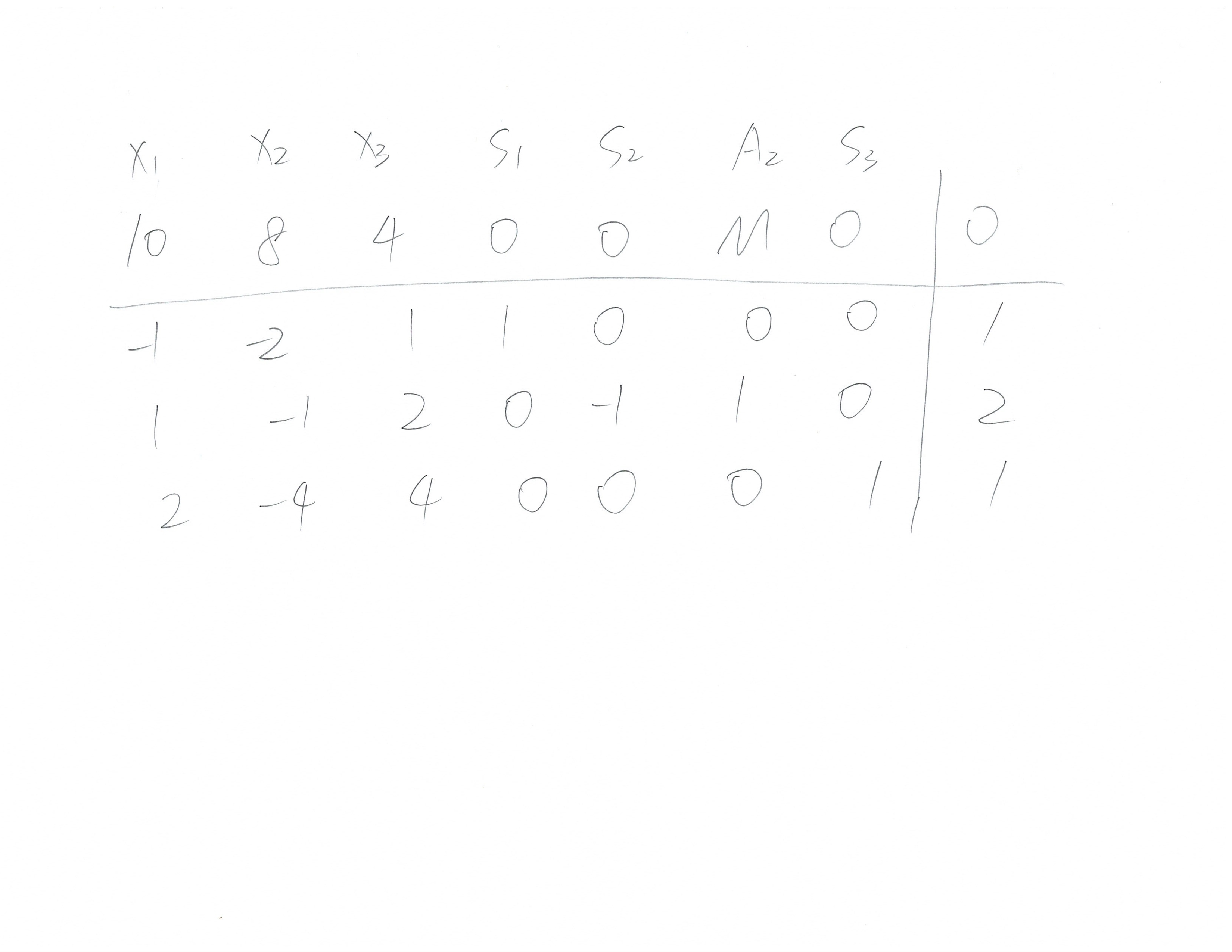
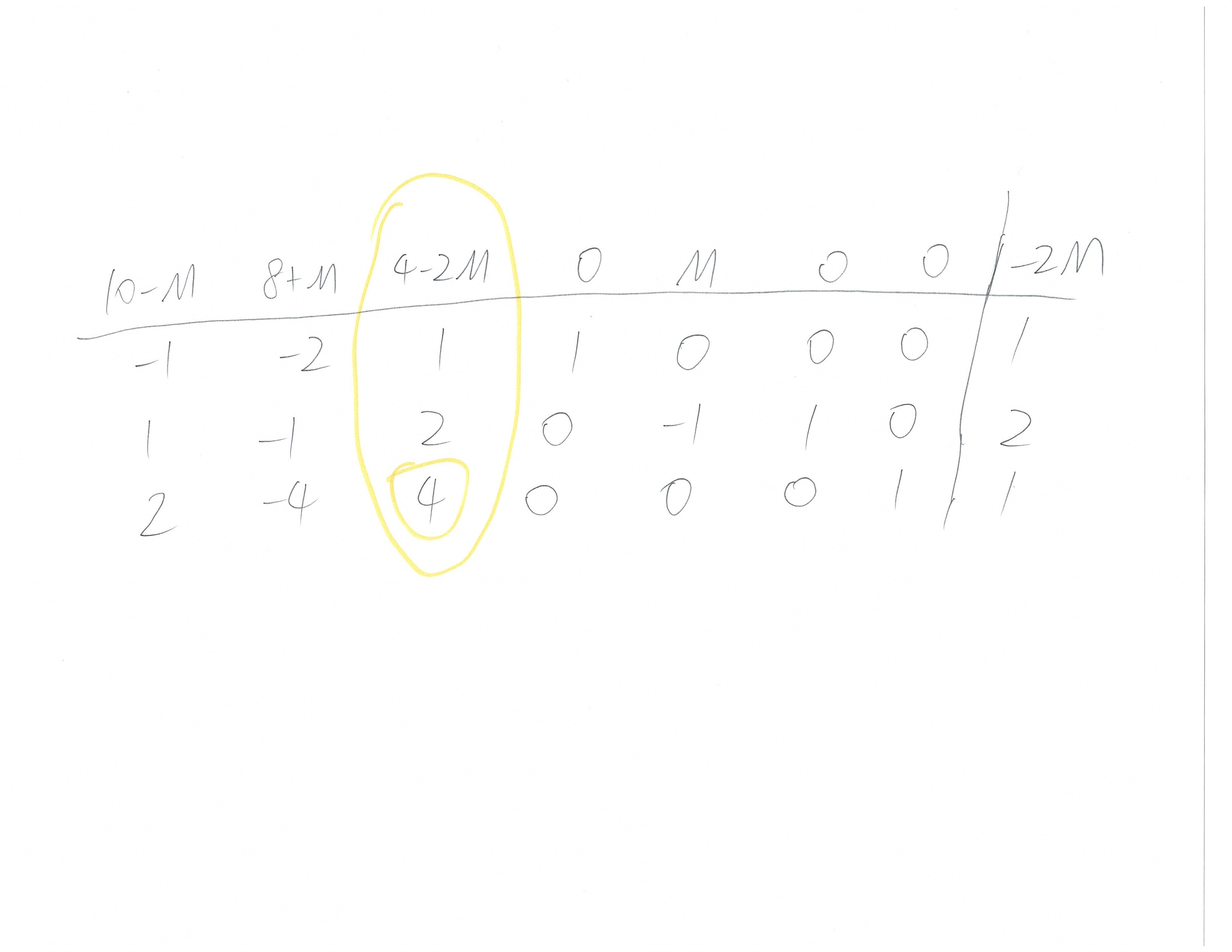
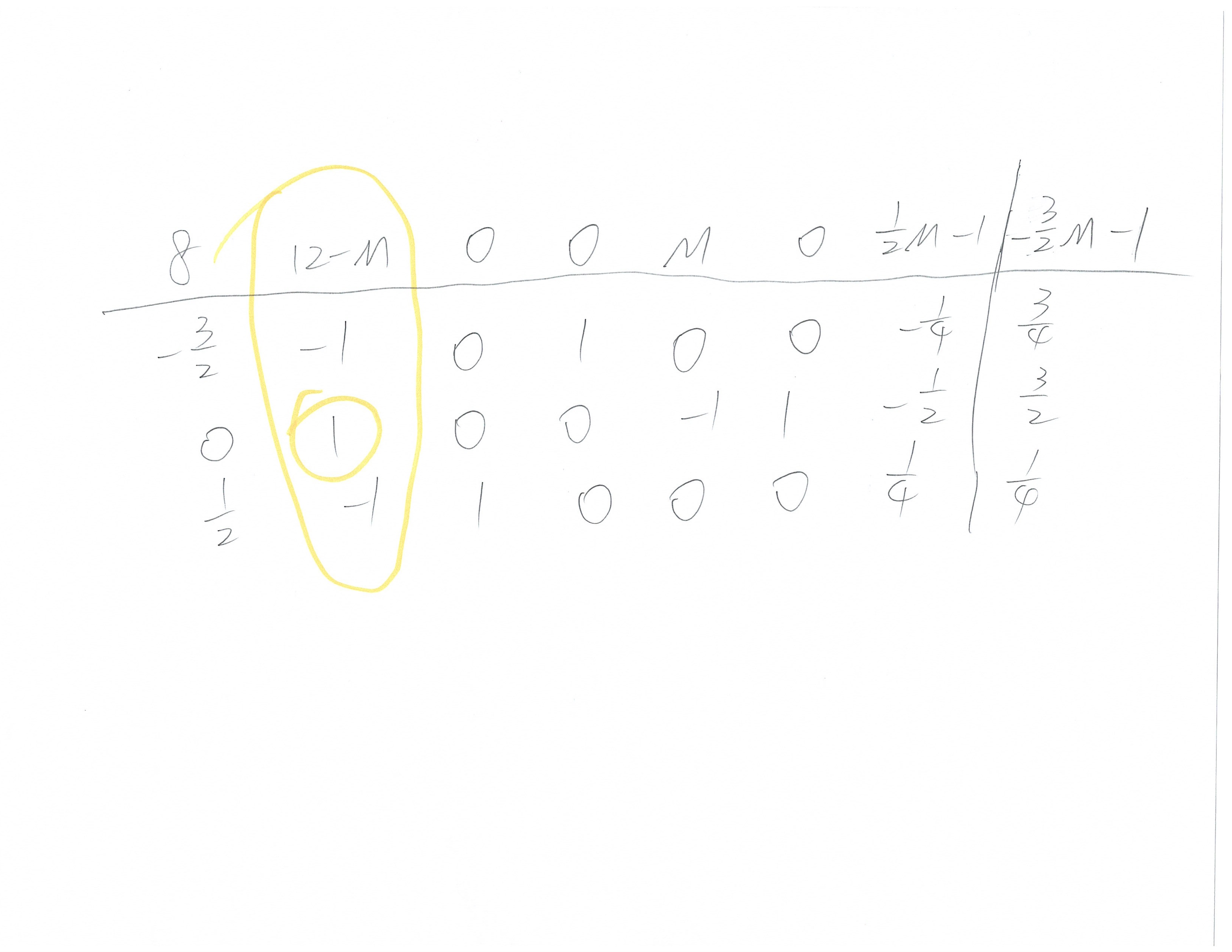
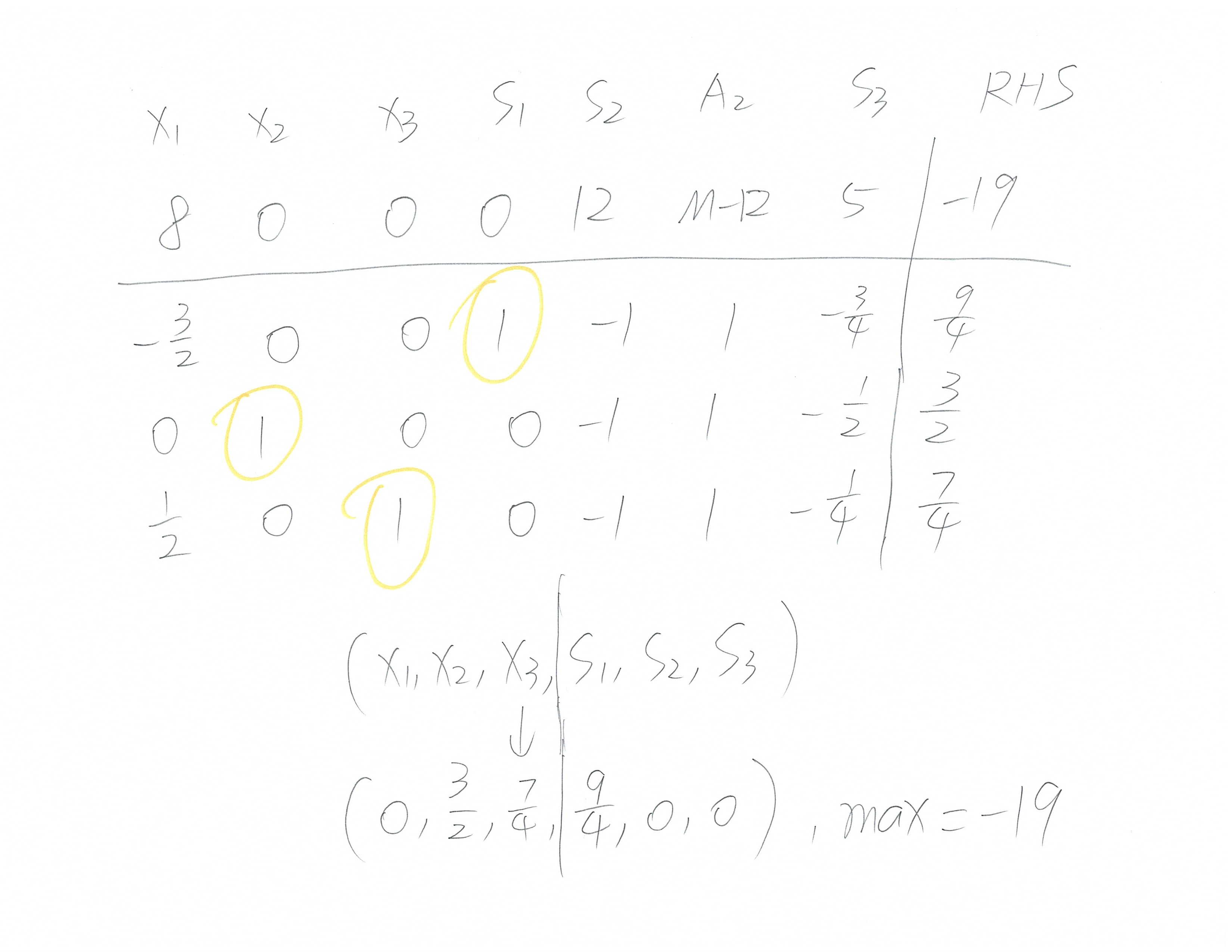
附上linprog.com的答案以供对比：
