This post was published in 2023-07-14. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
注意这个Assignment 3就做了两道题
注意这个assignment 3就做了两道题(3.6和3.9),后面的没做也没看
题目
直接开干Assignment 3,先看题再说
没准做Assignment 3的过程中还把Assignment 2不会做的那几道题搞会了
🔗 [Assignments | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/assignments/

Exercise 3.6
题目
Exercise 3.6

学习reduced cost
reduced cost
为什么看起来像是学过的样子,但查不到之前的笔记有写
查了下google,好像对应中文的 检验数
查询之前的笔记...🔗 [(2023年6月)Introduction to Linear Optimization学习笔记1 - Truxton's blog] https://truxton2blog.com/2023-06-intro-to-linear-optimization-learning-notes-1/

发现又忘得差不多了,很生气
花了很多时间跑回去写了一堆新的笔记

再杀回来看看这道题
latex草稿
所以本质上就是看公式3.1.4

注意,这里的reduced cost是反着写的,因为原书默认max()而不是min()
所以只需要把上面这张截图抄下来改写成max()的版本就可以了:
\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}
(a)
Since $x$ is a basic feasible solution, we have:
\[x=
\begin{bmatrix}
x_B \\
x_N
\end{bmatrix}
=
\begin{bmatrix}
x_B \\
0
\end{bmatrix} \]
Since $Ax=b$, we have
\[
x=
\begin{bmatrix}
B^{-1}b \\
0
\end{bmatrix}
\]
and corresponding destination value at $x$ is : $f(x)=c_B B^{-1} b$.
Assuming we have another solution (don't have to be feasible), we have
\[
f^{\prime}=f(x)-\sum_{\text{column}\ j\in N}(z_j-c_j)x_j
\]
Since we are assuming the reduced cost of every nonbasic variable $z_j-c_j$ is positive, we can't make $f^{\prime}>f(x)$ for any possible $x_j>0$ changes.
\par
(b)According to (a)'s result, if $x$ is assumed to be the unique optimal and nondegenerate solution, we have \[f^{\prime}
> f(x)-\sum_{\text{column}\ j\in N}(z_j-c_j)x_j\]
So
\[\sum_{\text{column}\ j\in N}(z_j-c_j)x_j > 0 \]
Since we must have $x\geq 0$ for every possible feasible solution, we have $z_j-c_j>0$ for all available index $j$, where index $j$ is the column index of non-basic solution area.
\end{document}
Exercise 3.9
题目
再看下一题:
Exercise 3.9

3.9(a)的latex草稿
3.9的(a)仍然是直接套书上的中间过程即可:
(*下面这个答案已经被反反复复改过很多个版本了,一开始的答案逻辑有点强行*)
\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}
(a) Assuming we are comparing any feasible solutions with a known basic feasible solution:
\[
\begin{aligned}
f & =\boldsymbol{c} \boldsymbol{x}=\left(\boldsymbol{c}_B, \boldsymbol{c}_N\right)\left[\begin{array}{c}
\boldsymbol{x}_{\boldsymbol{B}} \\
\boldsymbol{x}_N
\end{array}\right] \\
& =\boldsymbol{c}_B \boldsymbol{x}_{\boldsymbol{B}}+\boldsymbol{c}_N \boldsymbol{x}_N \\
& =\boldsymbol{c}_B\left(\boldsymbol{B}^{-1} \boldsymbol{b}-\boldsymbol{B}^{-1} \boldsymbol{N}_N\right)+\boldsymbol{c}_N \boldsymbol{x}_N \\
& =\boldsymbol{c}_B \boldsymbol{B}^{-1} \boldsymbol{b}-\left(\boldsymbol{c}_B \boldsymbol{B}^{-1} \boldsymbol{N}-\boldsymbol{c}_N\right) \boldsymbol{x}_N \\
& =f(x)-\sum_{j \in R}\left(\boldsymbol{c}_B \boldsymbol{B}^{-1} \boldsymbol{p}_j-c_j\right) x_j \\
& =f(x)-\sum_{j \in R}\left(z_j-\boldsymbol{c}_j\right) x_j
\end{aligned}
\]
as well as the collection of all zero-value reduced cost $I \subset R$.
If $I$ is empty, then we must have
\[
f(x)-\sum_{j \in R}\left(z_j-\boldsymbol{c}_j\right) x_j<f(x)
\]
, since we already have $x*$ associated basis matrix $B$ with all reduced cost nonnegative.
Therefore, $x^*$ is the only optimal solution.
\par
\end{document}
3.9(b)的思考
(b)暂时先摆在这里,能看多少看多少

符号:差集运算,Latex里面表示为\setminus
[mathjax-d]N \setminus I [/mathjax-d]意思是取所有包含在[mathjax]N[/mathjax]但不包含在[mathjax]I[/mathjax]的元素。
但3.9(b)的问题在于,目前我仍然认为这个(b)是理所当然,证了白证的东西
没有思路入手,就像证明1=1一样令人难过
必要与充分条件
Necessary and sufficient conditions
必要与充分条件
必要条件 necessary:无A就一定无B,则A是B的必要条件;
充分条件 sufficient:有A就一定有B,则A是B的充分条件;
充要条件 necessary and sufficient:有A就一定有B,无A就一定无B,则A是B的充要条件。
https://zhuanlan.zhihu.com/p/98996379
现在回到(a),我们先搞点不严谨的逻辑推理:
x*是optimal,I is empty -> x*的所有reduced cost都是>0的(否则x*就不是optimal了) -> x*无法再优化了,并且连得到另一个optimal solution的可能都没有,因为从f(x*)出发得到的所有f' 都比f(x*)要小。
x*是optimal,I is NOT empty -> x*存在reduced cost=0的成员 -> ???????
对着chatgpt说了半天,感觉还是搞不定这个问题,上google看看好了:
🔗 [optimization - Nonzero Reduced Cost in Linear Programming Optimal Solution Implies Uniqueness of Optimum? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/4546008/nonzero-reduced-cost-in-linear-programming-optimal-solution-implies-uniqueness-o
有关degeneracy的一些凌乱笔记
思路很凌乱,先把问题列出来
大概率和degenerated/退化解有关
而且涉及一个以前没怎么考虑过的概念:non-degenerated basic feasible solution对应的[mathjax]B[/mathjax](basis),以及feasible direction
疑问:在标准化Ax=b以后,三维空间有可能出现那种“一个顶点连着很多条边”的那种退化解顶点吗?
当然可能!
设想一种场景,3维空间的某个顶点其实是退化解,但我们目前学过的最简单的simplex algorithm只会从这个顶点出发尝试走2条边-对比2条边连接的2个顶点,还有1条边就暂时没办法管了。这个时候如果策略错了,就有可能出现循环,永远找不到最佳解...对吗?
也就是说,如果A=(B,N)步骤的basis没选好/选对,或者中途出了什么偏差,某些退化解可能会把优化的方向(走到下一个顶点的方向)带歪,可能会带到cycle里面去永远出不来了。
我是不是没搞懂degenerate的定义?有没有可能某个degenerate solution不满足2.11

等等,3维空间的x可以超过3维,因为Ax=b实际上的b的维度是可以变的,这种情况怎么想象?(比如想象一个5维的x在动,但是投影投在了3维空间上)
可以先用x+y+z=1这个书本上的例子来想象一下。
后续补充一张P85的图来解释上面的问题(退化解带偏了优化方向)

我突然发现我的(a)的思路有很大问题,因为我默认了这样一个逻辑:
已知x*是optimal solution,如果x*直接连接的所有顶点都比x*差(用判别数可以很容易求出这一点),那么x*就是唯一一个最优解...
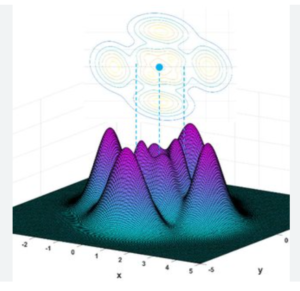
这个思路肯定是有问题的,考虑这样一个场景:另一个optimal solution藏在离x*很远的某个角落里:
但先别着急,下面这张图不是凸多面体,所以看看就好。目的是为了说明之前对(a)的证明不严谨。
后续补充:解决这个疑惑可能需要看看B.T书本中P86 有关Theorem 3.1的证明
Theorem 3.1(也是和degeneracy有关)
开始看这两段内容:
P86~P87


先看Theorem 3.1以及它的证明思路(证明要看,为了找出某些需要解决的“特例”反驳我之前对(a)的错误解法)
突然发现Theorem 3.1(a)的证明过程很熟悉,描述为:我原以为Theorem 3.1(a)需要一个全新的证明思路(经历了上面一堆奇怪思考的殴打),结果没想到证明过程就是这个无比熟悉的内容:

核心内容在于我又一次忘掉了这个强调的内容:

现在已知一个基本可行解x*,如果我能证明它比可行区域内的任何解(包括顶点代表的基本可行解,以及位于多面体内部的可行解)都优秀,那么它就是唯一的最优解。
Theorem 3.1(a)的证明其实和上面的(中文教材)思路完全一致,只是出发点略有改变:

再看Theorem 3.1(b)的内容以及证明思路

先想象一下:
If x is optimal and nondegenerate, then [mathjax]\bar c \geq 0[/mathjax]
What if x is optimal BUT degenerate? Any possible results for [mathjax]\bar c[/mathjax]?
Degeneracy:救救Vertex F
插入一个话题:救救Vertex F
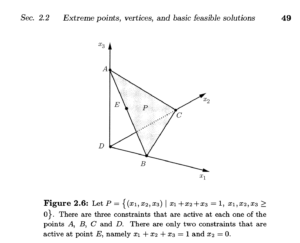
下面这张图在本笔记出现过一次了,再拉过来看看(人工标注了一个点H):
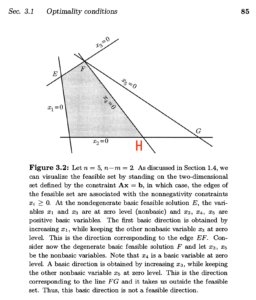
现在我从E到达了F,然后我在思考下一步该怎么走:
(使用当前学习的standard simplex algorithm)
走到E:这个肯定不行,不能回退的
走到G:如果真的走到G我们会发现x有一个元素<0,这个x是违规的,所以肯定不能走到G
走到H:从图上看确实可以,但要注意到一个严重的问题:F和H之间有3个不一样的数值
回忆一下常规的simplex algorithm:我们挑出一个0,把它变成>0的数值(入基),然后修改原本的基,让某个原先>0的数值缩小到0
但从F走到H,我们需要挑出2个0,把它变成>0的数值(入2个基),这可能不在当前学过的方法里面。
等待后续补充正规的从F走到H的方法。
后续补充:想了一下,应该是之前p=12119的部分手写笔记有问题,现在把p=12119的笔记更新了,并附带上这个问题正确的思考:


再次尝试做题(实际上到了最后3.9b还是没做出来)
再回来看之前的问题:
注意一下这个:

有点失望,因为P87

总的来说看到这里,某些一直放心不下的疑惑得到了解决(只要不是退化解,当前的很多证明问题都没那么难),但仍然不知道某些问题具体的证明方式(simplex algorithm为什么能避开退化解带来的问题?用什么方式解决的?)。
继续看到p87剩下的内容为止:

所以说目前(我)比较熟悉的那些内容都是默认永不出现degenerate情形的。一旦遇到degenerate就直接GG.
看看P92对于simplex algorithm处理degenerate的方法是怎么描述的:

看到pivot selection(而不是摄动法)似乎终于明白了,原来我一直搞不清楚这个问题的真正原因是我搞错了x_B的更新机制...
所以我马上杀回去修改之前的笔记:




所以再杀回去看看Exercise 3.9的(a)与(b)描述的不同:



先把所有可能讨论的情况列举出来:(针对x*)
不退化,唯一最优解
不退化,不唯一最优解
退化,唯一最优解
退化,不唯一最优解
在(a)或(b)的条件引入之前,单纯从3.9的题干信息来看,我们已经知道了:
- x*是optimal,有optimal basis
- 所以x*所有判别数都>=0(根据Definition 3.3以及一系列前置定理)
- 现在讨论x*是不是only optimal
- x*有可能不是only optimal:如果存在判别数=0(只要有1个就有机会让x*不唯一optimal,2个也有机会,3个也有机会...)
- 但3.9的(a)指定了“不存在为0的判别数”,断绝了(4)的任何机会,所以x*现在肯定是only optimal,所以3.9的(a)逻辑就通了
- 现在离开3.9(a),条件更艰苦一点:就算判别数有0,通过更加严格的判定条件,也可以让x*一定是唯一的optimal,断绝了(4)的任何机会.
先放一张中途草稿,注意这张草稿可能问题很大(尤其是涉及到退化解的那部分)
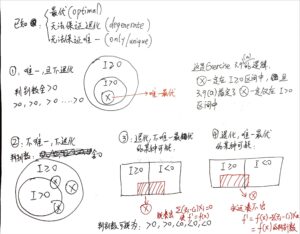
或者说,干脆从3.9(b)入手,看看能不能改对上面这张图的③和④