MIT 6.251J Introduction To Mathematical Programming学习（2023-07-14，Assignment 2的相关笔记）

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

Table of Contents

题目

Assignment1的1.11做的我很生气，但还是赶紧来做A2吧

🔗 [Assignments | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/assignments/

对应第2章

不妙，似乎是卡在入门知识和simplex algorithm之间了

Exercise 2.6

题目

2.6

完全没办法做，只能从书的第42页开始看

超平面，半空间，凸集，凸包，极点等一些前置知识的学习

欠的东西有点多，只能写一堆垃圾先了

多面体：polyhedron

多面体的复数：polyhedrons，或者polyhedra，B.T.这本书里用的是polyhedra

🔗 [多面体 - 维基百科，自由的百科全书] https://zh.wikipedia.org/wiki/多面体

如果只看维基百科：

多面体属于多胞体的一种特殊类型：通常来说默认是3维空间（2维空间和>3维的高维空间则使用多胞体的一般称呼）

但事实上，在B.T.这本书里，polyhedron=多胞体：

p43

对于hyperplane和halfspace，补充了一些笔记在🔗 [（2023年6月）Introduction to Linear Optimization学习笔记1 - Truxton's blog] https://truxton2blog.com/2023-06-intro-to-linear-optimization-learning-notes-1/

蓝色的部分讲述了vector[mathjax]a[/mathjax]和hyperplane垂直的证明方法

后续p44也有一张图：

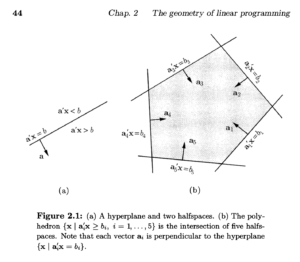
符号

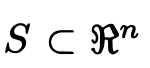
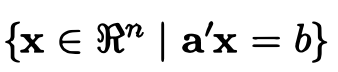
接下来看Convex Sets

这部分之前应该学过类似的

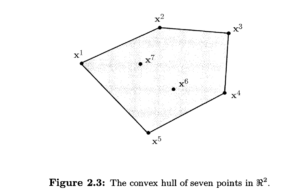
这部分内容的理解稍后补充

convex combination：凸组合

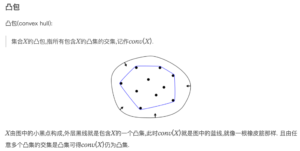
convex hull：凸包

对凸包的进一步理解：

书上有对这4条定理的证明 p45

注意在(b)的证明里有一条需要注意的定义：

后面会提到，extreme point和vertex，以及基本可行解，是同一个东西（p52~p53）

概念有点多，不知道是从题目入手还是把书的第二章看完再说

🔗 [凸集常用性质 | swt's blog] https://swt-2020.github.io/2020/11/07/凸集常用性质/

仿射，多面体、非多面体、凸包、锥、锥包、凸锥、紧/紧致/紧空间等一些前置知识

学了一些前置知识，试图重新理解这道题，（当然是失败了），所以又开始准备一堆前置知识

回到2.6这道题本身：

事实上，如果用之前学过的矩阵的秩来理解，似乎要理解(a)并不难（并不是严格证明），大致意思就是说：

对于一个m x n的非方矩阵，如果m>n，则矩阵的任意一列一定可以用至多m列的线性组合表示。这是肯定的，因为矩阵的秩最多最多只有n，矩阵的任意一列一定可以用n列的线性组合表示；由于m>n，则显然满足(a)。最极端的情况下只需要使用n列线性组合表达（每一列对应的系数都>0），n<m，满足要求。

对于一个m x n的非方矩阵，如果m<n，则矩阵的秩最多最多只有m，矩阵的任意一列一定可以用m列的线性组合表示，也满足(a)。最极端的情况下只需要使用m列线性组合表达（每一列对应的系数都>0）。

但上面这个理解存在一个问题：矩阵的秩的定义里提到的“线性组合表达”没有约束线性组合的系数都>=0，所以上面的理解内容只能作为一个理解的思路。

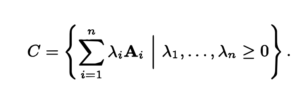
这里其实涉及到“锥包”的内容，锥包/锥/锥形组合 = 非负线性组合 = conic combination，所以上面的式子简写为C.

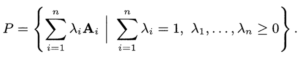
这个才是凸包，不仅要求非负线性组合，还要求系数之和为1. 比如这个

再加上一个Affine combination

(a)的中文翻译如下：来自 🔗 [凸集常用性质 | swt's blog] https://swt-2020.github.io/2020/11/07/凸集常用性质/

🔗 [【非线性优化】凸锥、对偶锥及极锥 - 知乎] https://zhuanlan.zhihu.com/p/553654610

一个“锥”（Cone）到底应该怎么理解？

“锥“是不闭合的无限空间。所以类似“三维空间的一个圆锥体“，”三维空间的一个四面体“ 都不是锥.

看这篇博客理解的：🔗 [Andy Jones] https://andrewcharlesjones.github.io/journal/convex-cones.html

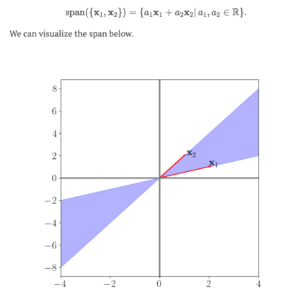
上面这张图到底有几个锥呢？可以这样说：位于第一象限的紫色区域[mathjax]A_1[/mathjax]是一个convex cone；位于第三象限的紫色区域[mathjax]A_3[/mathjax]是一个convex cone；两个紫色区域的并集[mathjax]A_1 \cup A_3[/mathjax]是一个cone，但并不convex，所以是一个convex-cone. （灵感来自https://math.stackexchange.com/a/345904）

有点迷糊，先理清一下多面体、非多面体、凸包、锥、锥包、凸锥、紧/紧致/紧空间（等概念）的包含关系

多胞体 Polyhedra：要求平面

多面体Polytope：首先要求是多胞体Polyhedra，其次要求多胞体Polyhedra有界（Bounded）

下面这张图来自LP and network flows, p75

凸 convex：要求任意两点连线也在集合中

锥 cone：首先锥一定有一个“原点”，其次：见上面的笔记

闭 close：似乎超出当前学习的范畴了（实分析、凸优化）：

一些和“闭”有关的讨论：

🔗 [real analysis - How do you prove that ${ Ax \mid x \geq 0 }$ is closed? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/1831401/how-do-you-prove-that-ax-mid-x-geq-0-is-closed

🔗 [real analysis - Can we say a convex cone is a closed set without further proof? - Mathematics Stack Exchange] https://math.stackexchange.com/questions/1819332/can-we-say-a-convex-cone-is-a-closed-set-without-further-proof

包：hull

锥包：conic hull，暂时找不到很好的很直观的例子，少有的网页见🔗 [Convex and conic hull] https://inst.eecs.berkeley.edu/~ee127/sp21/livebook/def_cvx_hull.html

紧：compact

比如在这张图里：（这张图来自🔗 [general topology - Visual representation of difference between closed, bounded and compact sets - Mathematics Stack Exchange] https://math.stackexchange.com/questions/3223408/visual-representation-of-difference-between-closed-bounded-and-compact-sets，不保证正确，因为讨论度很低+这是提问题的人画的）

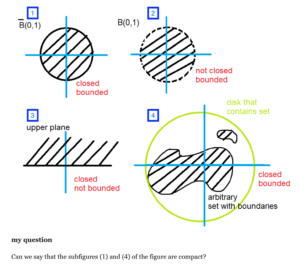
（小图）1和4就是紧致的，因为它们闭合且有界。

胡乱做一下2.6

再回到2.6这道题的第(a)问：

可以用一个画图的例子来帮助理解：

假设在二维空间的第一象限随便画了3个点，现在要绘制这3个点形成的convex combination区域，以及conic combination区域

绘制conic combination的时候很自然就发现了，一开始绘制的（红色，A和B）完全覆盖了后面绘制的（A和C，以及B和C）：

（扫描出了点问题，其实整张图都是蓝色和红色，没有黑色，浏览顺序为从左到右，从上到下）

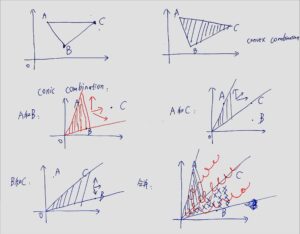
相当于到了最后合并的时候我们发现，C点对conic combination区域的绘制没有影响/帮助。

二维空间m=2，conic combination使用m=2个vector来表达（系数>0），同时令第3个vector的系数为0

和2.6的(a)能对上一点关系

突然发现如果直接看定理2.4：

就能“证明”2.6的(a)了

先空着，等搞完2.6(b)以后再来填充

如果这样看的话甚至(b)也很好懂了，虽然最终的结果有点令人不满（如果仅仅是从功利的解题角度来看确实如此），但还是先用这个答案凑合一下吧：

先画张草稿，(b)其实就是在(a)的矩阵A的底下多增了一行全是1的行，这样整个矩阵乘法就满足“convex hull“的定义了，由于行数变成了m+1，所以根据定理2.4，有m+1个线性无关的列。

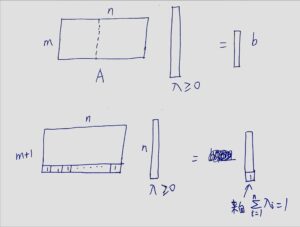
latex草稿

写点latex草稿：

\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}


(a) If we regard the conic collection of $A_1, \cdots , A_n$ as a $m\times n$ matrix $A$, then the conic combination ($C$) satisfies the equation in Theorem 2.4, $A\lambda=y$ and $y$>=0. According to Theorem 2.4, there are $m$ columns in matrix $A$ linearly independent. So  we can proof that any element of matrix $A$ can be expressed with those $m$ columns' linear combination, with at most $m$ of the linear combination's coefficients being nonzero.
\par
(b) Starting from the matrix $A$ in the previous solution (a), we can add an additional row of all ones to the bottom of matrix $A$: $A \rightarrow  \begin{bmatrix} A \\ 1 \end{bmatrix} = A^{\prime} $, then the convex hull $P$ can be expressed as $A^{\prime}\lambda= \begin{bmatrix} y \\ 1 \end{bmatrix}$. According to Theorem 2.4, there are $m+1$ columns linearly independent. So  we can proof that any element of matrix $A^{\prime}$ can be expressed with those $m+1$ columns' linear combination, with at most $m+1$ of the linear combination's coefficients being nonzero.


\end{document}

截图：

Exercise 2.7

简单的理解和分析

看看下一题：

Exercise 2.7

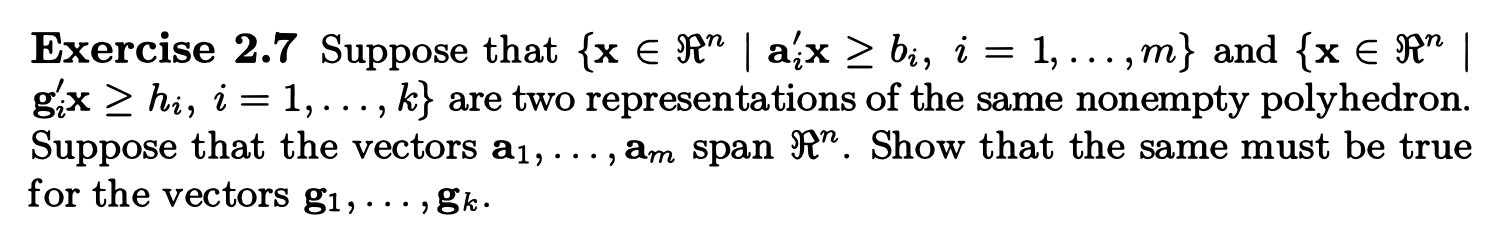
注意，由于现在以做题为主，所以跳过了对p43~p63很多定义/定理的仔细阅读（也就是说，一眼看上去很合理，没有什么看不明白的东西）

现在看到p63的Theorem 2.6

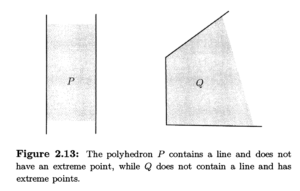
注意这个(b)，因为第一眼看上去很令人疑惑不解。书中有一张图进行了解释：

chatgpt

“多面体P不包含线”这句话的含义是，在这个多面体P中，没有一条完整的直线完全落在这个多面体内部。

在更技术性的语言中，这就是说多面体P没有任何方向可以让你无限远地移动而仍然保持在多面体内部。换句话说，不论你在多面体内选择何处作为起点，你总能找到一个“边界”，超过这个边界，你就不再位于多面体内部。

这个性质对于定义有界多面体（bounded polyhedron）和无界多面体（unbounded polyhedron）非常重要。有界多面体是指它不包含任何完整的直线，也就是说，你不能在它内部任意远地移动而仍然保持在多面体内部。相反，无界多面体是指它内部存在一条（或多条）可以沿着无限远移动的直线。

例如，在二维空间中，一个闭合的多边形（如一个三角形或一个正方形）就是一个有界多面体，因为你不能在其内部无限远地移动。而一个单侧无限扩展的直角三角形，则是一个无界多面体，因为你可以沿着它的一个边无限远地移动。

这个定理来的很突然，只要有至少1个极点，就能直接判定矩阵的秩为空间维度n，直接行满秩了。

latex草稿

所以Exercise 2.7直接套Theorem 2.6就可以，同时Theorem 2.5也可以作为反证的例子：

\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}


Since we already known the vectors $a_1, \cdots , a_m$ span $\Bbb R^n$, the nonempty polyhedron satisfies the (c) equivalent condition in Theorem 2.6. Therefore, for $g_i x \geq h_i$, there must exist $n$ vectors linearly independent: $g_1, \cdots, g_k$ span $\Bbb R^n$.


\end{document}

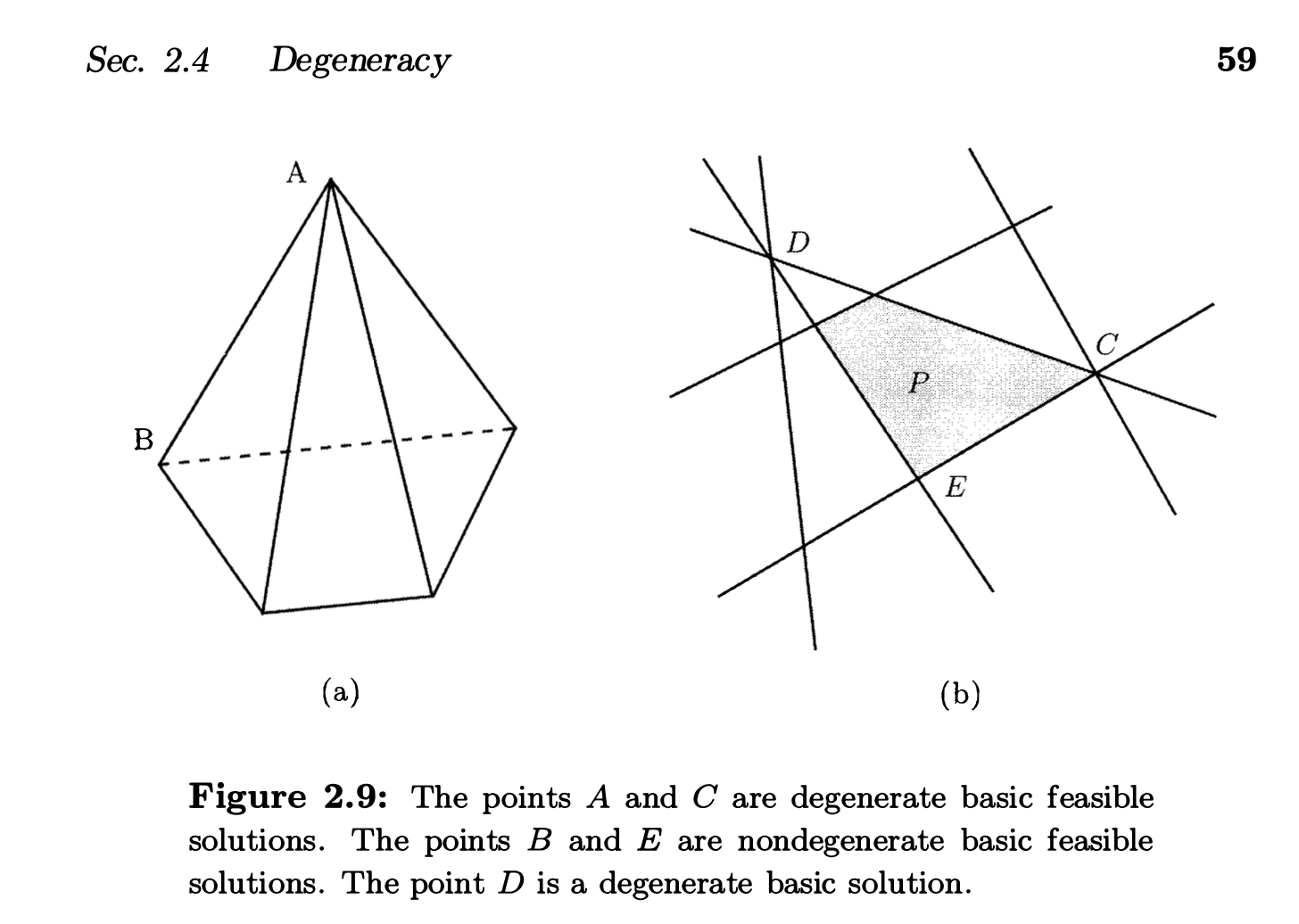
Exercise 2.9

题目

再看下一题 2.9

degenerate/Degeneracy/base（前置学习）

也就是退化解/基解

概念：degenerate/Degeneracy

p58 章节2.4

好像很容易懂，只需要理解 active constraints 是什么就可以搞明白了。

比如一个不等式约束了[mathjax]x_1+x_2+x_3<=10[/mathjax]，然后我有2组解[mathjax]x_1=(3,3,4),\ x_2=(1,1,1)[/mathjax]，这个时候对于解[mathjax]x_1[/mathjax]而言，约束[mathjax]x_1+x_2+x_3<=10[/mathjax]就属于active constraints，因为3+3+4=10，正好卡在不等式的临界点；对于解[mathjax]x_2[/mathjax]而言，约束[mathjax]x_1+x_2+x_3<=10[/mathjax]就不属于active constraints，因为1+1+1=3，离约束的边界还很远。

两个例子：

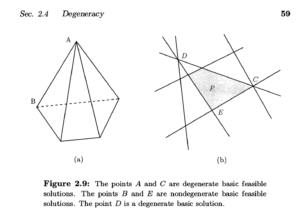
然后是Definition 2.11

把 🔗 [（2023年6月）Introduction to Linear Optimization学习笔记1 - Truxton's blog] https://truxton2blog.com/2023-06-intro-to-linear-optimization-learning-notes-1/ 的笔记搬过来补充一下：

基解：[mathjax][2,2,-1,-3,5, \vdots \ 0,0,0,0,0][/mathjax]

退化的基解：[mathjax][2,2,-1,-3,0, \vdots \ 0,0,0,0,0][/mathjax]

可行解：[mathjax][2,0,10,2,5, \vdots \ 0,0,2,0,3][/mathjax]

基可行解：[mathjax][3,5,10,2,9, \vdots \ 0,0,0,0,0][/mathjax]

好像漏看了一个概念：base

在这里的base就是指能张成空间维度m的m个向量，这m个向量线性无关。

或者说，base的作用就是：

（在m维空间中）挑选出m列线性不相关的vectors组成一个m x m的方阵[mathjax]A^{\prime}[/mathjax]（方阵的秩为m），然后这个方阵用来解[mathjax]A^{\prime}x^{\prime}=b[/mathjax]，得到的解[mathjax]x^{\prime}[/mathjax]加上(n-m)个0就构成了一个基本可行解。

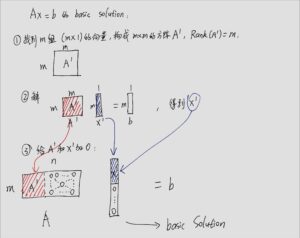
如何区分2个base是不同的base？至少要有1列不同。那为什么两个不同的bases乘以同一个x还能得到相同的结果？说明那个“至少有1列不同”的那1列（或者导致bases不同的那几列）都被0搞没了。0来自哪里？来自x . x有0说明什么？说明x对应的basic solution至少有(n-m+1)个0，是退化的。

latex草稿

\documentclass{article}
\usepackage{mathtools,amssymb}
\begin{document}

(a)
Suppose we have two different bases $A$ and $A^{\prime}$, with Rank($A$)=m and Rank($A^{\prime}$)=m. These two bases are different, indicating they have at least 1 different column. To make $Ax=b$ and $A^{\prime}x=b$, we need to use zeros to nullify the different columns. Since $x$ has at least zero value, we can say the basic solution is degenerate.
\par
(b)
No. Consider this example:
\begin{math}
  \left\{
    \begin{array}{l}
      x+y+z=0\\
      x+y-z=0 \\
      x-y-z=0 \\
      x,y,z\geq 0
    \end{array}
  \right.
\end{math}
\par
This example only creates one base: 
$ \begin{bmatrix}
1 & 1 & -1 \\
1 & -1 & -1 \\
1 & -1 & 1 
\end{bmatrix}  $ as well as one degenerate basic solution: 
$ \begin{bmatrix}
0 \\
0 \\
0 
\end{bmatrix}  $.
\par
(c)No. We can re-use the counterexample in (b), in which there's only one degenerate basic solution 
$ \begin{bmatrix}
0 \\
0 \\
0 
\end{bmatrix}  $.

\end{document}

Exercise 2.13, 2.20, 2.22（跳过）

再看下一题：

Exercise 2.13

保留很大疑问（尤其是对(a)），暂时先放一边了

2.20和2.22

先跳过

编程题

先杀回前几天的编程题，把AMPL埋了

🔗 [Formulations] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/72668234e7184363ade764713fac5bfc_MIT6_251JF09_lec01.pdf

第8页

import pandas as pd

df = pd.read_csv(
    "./ocw.mit.edu_courses_6-251j-introduction-to-mathematical-programming-fall-2009_6017d80f7a46f01478e88915b175b6b6_data.txt",
    sep="\t")
# structure: t	D	E	c	n
t_arr = df['t'].values
D_arr = df['D'].values
E_arr = df['E'].values
c_arr = df['c'].values
n_arr = df['n'].values

# print(len(t_arr))
from pulp import *

prob = LpProblem("demo", LpMinimize)

lp_vars_x = []
for i in range(1, 71):
    lp_vars_x.append(LpVariable("x" + str(i)))
lp_vars_y = []
for i in range(1, 71):
    lp_vars_y.append(LpVariable("y" + str(i)))
lp_vars_w = []
for i in range(1, 71):
    lp_vars_w.append(LpVariable("w" + str(i)))
lp_vars_z = []
for i in range(1, 71):
    lp_vars_z.append(LpVariable("z" + str(i)))

prob += sum(ci * xi for ci, xi in zip(c_arr, lp_vars_x)) + sum(ni * yi for ni, yi in zip(n_arr, lp_vars_y))

lp_vars_w = []
for i in range(1, 20):
    temp = None
    for j in range(1, i + 1):
        temp += lp_vars_x[j - 1]
    lp_vars_w.append(temp)
for i in range(20, 71):
    temp = None
    for j in range(i, min(i + 20, 71)):
        temp += lp_vars_x[j - 1]
    lp_vars_w.append(temp)

lp_vars_z = []
for i in range(1, 15):
    temp = None
    for j in range(1, i + 1):
        temp += lp_vars_y[j - 1]
    lp_vars_z.append(temp)
for i in range(15, 71):
    temp = None
    for j in range(i, min(i + 15, 71)):
        temp += lp_vars_y[j - 1]
    lp_vars_z.append(temp)

for i in range(0, 70):
    prob += lp_vars_w[i] + lp_vars_z[i] + E_arr[i] >= D_arr[i]
    prob += 0.2 * (lp_vars_w[i] + lp_vars_z[i] + E_arr[i]) >= lp_vars_z[i]
    prob += lp_vars_x[i] >= 0
    prob += lp_vars_y[i] >= 0
    prob += lp_vars_w[i] >= 0
    prob += lp_vars_z[i] >= 0

prob.solve()

print("Status:", LpStatus[prob.status])

for v in prob.variables():
    print(v.name, "=", v.varValue)

print('minimum result: ' + str(value(prob.objective)))

注意：

代码跑起来了，但我真的不知道答案对不对
输出的变量排序不太对（比如x_9会排在x_70的前面），懒得改了，以后再说

运行结果：

Welcome to the CBC MILP Solver
Version: 2.10.3
Build Date: Dec 15 2019

command line - /root/miniconda3/envs/py311/lib/python3.11/site-packages/pulp/solverdir/cbc/linux/64/cbc /tmp/7528319864eb405ab0c60bff23af49e3-pulp.mps timeMode elapsed branch printingOptions all solution /tmp/7528319864eb405ab0c60bff23af49e3-pulp.sol (default strategy 1)
At line 2 NAME          MODEL
At line 3 ROWS
At line 425 COLUMNS
At line 6286 RHS
At line 6707 BOUNDS
At line 6848 ENDATA
Problem MODEL has 420 rows, 140 columns and 5720 elements
Coin0008I MODEL read with 0 errors
Option for timeMode changed from cpu to elapsed
Presolve 139 (-281) rows, 140 (0) columns and 3718 (-2002) elements
0  Obj 0 Primal inf 169590.37 (69)
55  Obj 591676.33 Primal inf 24838.294 (48)
120  Obj 736055.18
Optimal - objective value 736055.18
After Postsolve, objective 736055.18, infeasibilities - dual 0 (0), primal 0 (0)
Optimal objective 736055.1767 - 120 iterations time 0.002, Presolve 0.00
Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.01   (Wallclock seconds):       0.02

Status: Optimal
x1 = 0.0
x10 = 0.0
x11 = 51.612
x12 = 71.05
x13 = 70.74
x14 = 70.43
x15 = 0.0
x16 = 0.0
x17 = 0.0
x18 = 0.0
x19 = 0.0
x2 = 0.0
x20 = 0.0
x21 = 0.0
x22 = 0.0
x23 = 0.0
x24 = 0.0
x25 = 0.0
x26 = 0.0
x27 = 0.0
x28 = 0.0
x29 = 0.0
x3 = 0.0
x30 = 0.0
x31 = 0.0
x32 = 0.0
x33 = 0.0
x34 = 0.0
x35 = 0.0
x36 = 0.0
x37 = 0.0
x38 = 0.0
x39 = 332.542
x4 = 0.0
x40 = 57.378
x41 = 62.602
x42 = 62.304
x43 = 62.018
x44 = 61.748
x45 = 61.46
x46 = 61.192
x47 = 60.932
x48 = 60.664
x49 = 60.406
x5 = 0.0
x50 = 135.82
x51 = 135.29
x52 = 134.8
x53 = 134.29
x54 = 65.12
x55 = 0.0
x56 = 0.0
x57 = 0.0
x58 = 0.0
x59 = 317.984
x6 = 0.0
x60 = 115.224
x61 = 120.23
x62 = 119.72
x63 = 119.244
x64 = 118.772
x65 = 118.292
x66 = 117.834
x67 = 117.39
x68 = 116.942
x69 = 116.502
x7 = 0.0
x70 = 3193.342
x8 = 0.0
x9 = 0.0
y1 = 149.26
y10 = 71.69
y11 = 19.748
y12 = 0.0
y13 = 0.0
y14 = 0.0
y15 = 0.0
y16 = 0.0
y17 = 0.0
y18 = 0.0
y19 = 0.0
y2 = 0.0
y20 = 0.0
y21 = 0.0
y22 = 0.0
y23 = 0.0
y24 = 0.0
y25 = 433.7405
y26 = 0.0
y27 = 0.0
y28 = 0.0
y29 = 388.3075
y3 = 74.08
y30 = 69.84
y31 = 69.55
y32 = 69.25
y33 = 68.97
y34 = 0.0
y35 = 11.052
y36 = 5.568
y37 = 5.596
y38 = 5.622
y39 = 5.652
y4 = 73.72
y40 = 439.4205
y41 = 5.708
y42 = 5.738
y43 = 5.766
y44 = 394.1015
y45 = 0.0
y46 = 0.0
y47 = 0.0
y48 = 0.0
y49 = 0.0
y5 = 73.37
y50 = 75.972
y51 = 70.278
y52 = 70.116
y53 = 69.952
y54 = 84.35
y55 = 445.5445
y56 = 11.86
y57 = 11.922
y58 = 11.98
y59 = 400.3475
y6 = 73.02
y60 = 6.278
y61 = 6.308
y62 = 6.342
y63 = 6.372
y64 = 6.404
y65 = 0.0
y66 = 0.0
y67 = 0.0
y68 = 0.0
y69 = 0.0
y7 = 72.68
y70 = 1419.068
y8 = 72.34
y9 = 72.01
minimum result: 736055.1767000002

以后再说！