This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.Table of Contents
使用big-M转换一些无法直接tableau的问题
如果遇到长得非常奇怪的maximize/minimize LP，比如这个LP的对偶问题，甚至连传统tableau的第一步都无法进行，该怎么办呢？
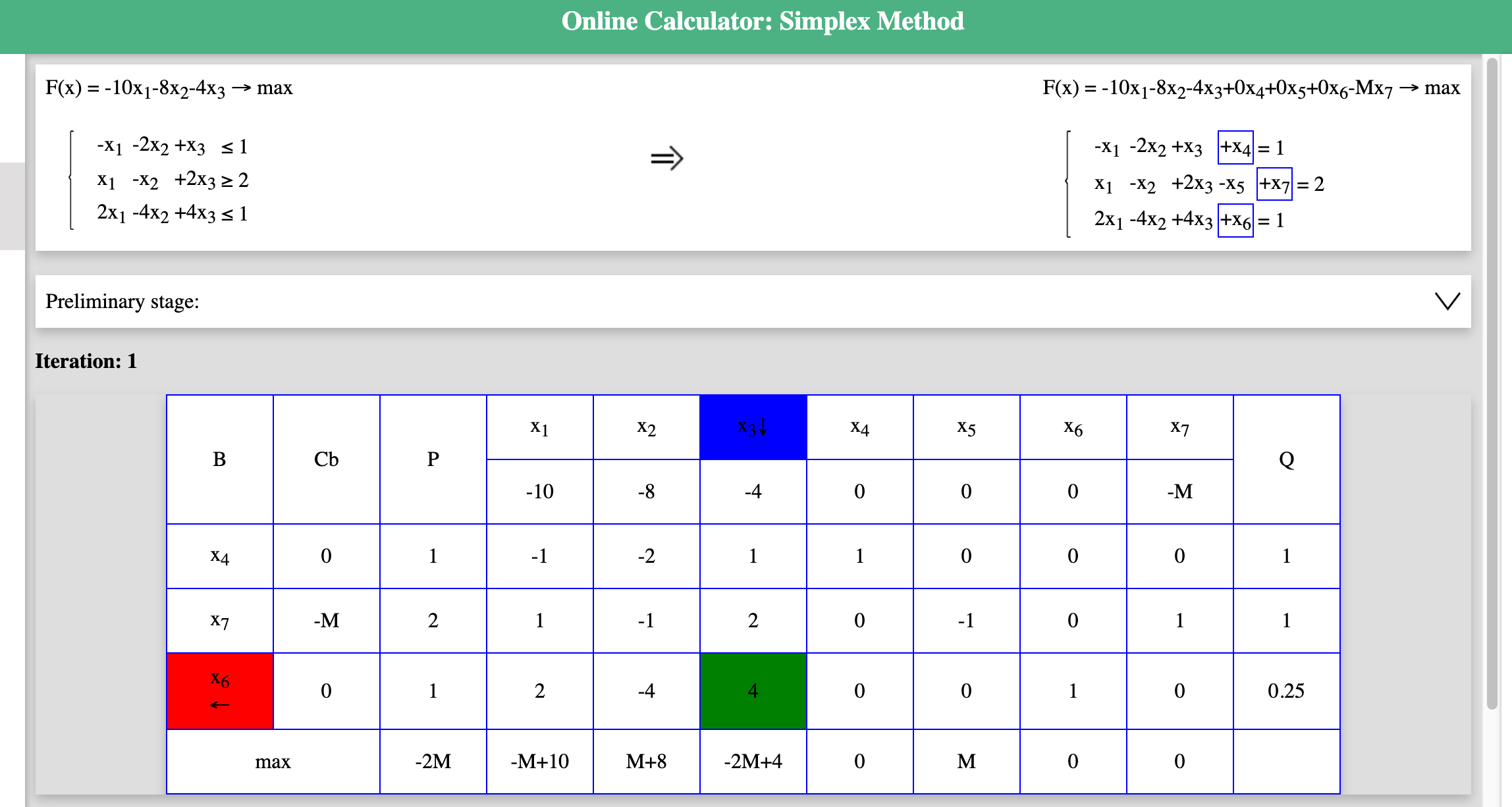
使用big-M法！具体写在另一个笔记里：🔗 [使用big-M解决一些无法直接tableau的LP问题 - Truxton's blog] https://truxton2blog.com/lp-unusual-tableau-bigm-conversion/
标准方法
这里原本挂着两个cs.emory.edu的链接，但这两个链接似乎对我的学习造成了非常巨大的困扰，所以删除这两个链接并不再访问（如果一定要追溯原链接，还可以在draft/autosave里面找到），现在重新来整理一遍（大概是修正过的）tableau方法：
maximize类型：
- 第一行所有系数都>=0则停止计算（已经最优）
- 如果条件（1）不满足，则还需要进一步优化：从第一行系数中挑出最小的数值（由于不是最优，所以这个最小的数值肯定是个负数）作为pivot column
- 从pivot column里面挑出拥有最小[mathjax]\frac{\text{RHS}}{a_{ij}}[/mathjax]的那一行作为pivit row（注意这里RHS>0，所以只挑出[mathjax]a_{ij}>0[/mathjax]的系数进行计算；负数的系数会被跳过）*如果在仅有的那个pivot column里面，所有的系数都非正，那说明了什么？说明了optimal unbounded，见后面补充的笔记
- 用pivot column和pivot row确定需要enter basis的变量
- 把这个变量设为1（一整行除以系数就可以）；然后用row elimination的方法把这个变量的一整列都变成0（除了这个变量为1，其他的都是0）
- 回到第1步的判断
minimize类型：
除了标红的不一样，其他的似乎都一样
- 第一行所有系数都<=0则停止计算（已经最优）
- 如果条件（1）不满足（存在>0的系数），则还需要进一步优化：从第一行系数中挑出最大的数值（由于不是最优，所以这个最大的数值肯定是个正数）作为pivot column
- 从pivot column里面挑出拥有最小[mathjax]\frac{\text{RHS}}{a_{ij}}[/mathjax]的那一行作为pivit row（注意这里RHS>0，所以只挑出[mathjax]a_{ij}>0[/mathjax]的系数进行计算；负数的系数会被跳过）*如果在仅有的那个pivot column里面，所有的系数都非正，那说明了什么？说明了optimal unbounded，见后面补充的笔记
- 用pivot column和pivot row确定需要enter basis的变量
- 把这个变量设为1（一整行除以系数就可以）；然后用row elimination的方法把这个变量的一整列都变成0（除了这个变量为1，其他的都是0）
- 回到第1步的判断
maximize例题
maximize的例题是2024-10-26补充的，LP早就忘的差不多了，所以补充的内容可能含有返祖知识
题目来自🔗 [personal.utdallas.edu/~scniu/OPRE-6201/documents/LP06-Simplex-Tableau.pdf] https://personal.utdallas.edu/~scniu/OPRE-6201/documents/LP06-Simplex-Tableau.pdf
（pdf的备份贴在下面）
前面几步（包括LP表达式的转换，tableau的建立，以及pivot的第一步）：
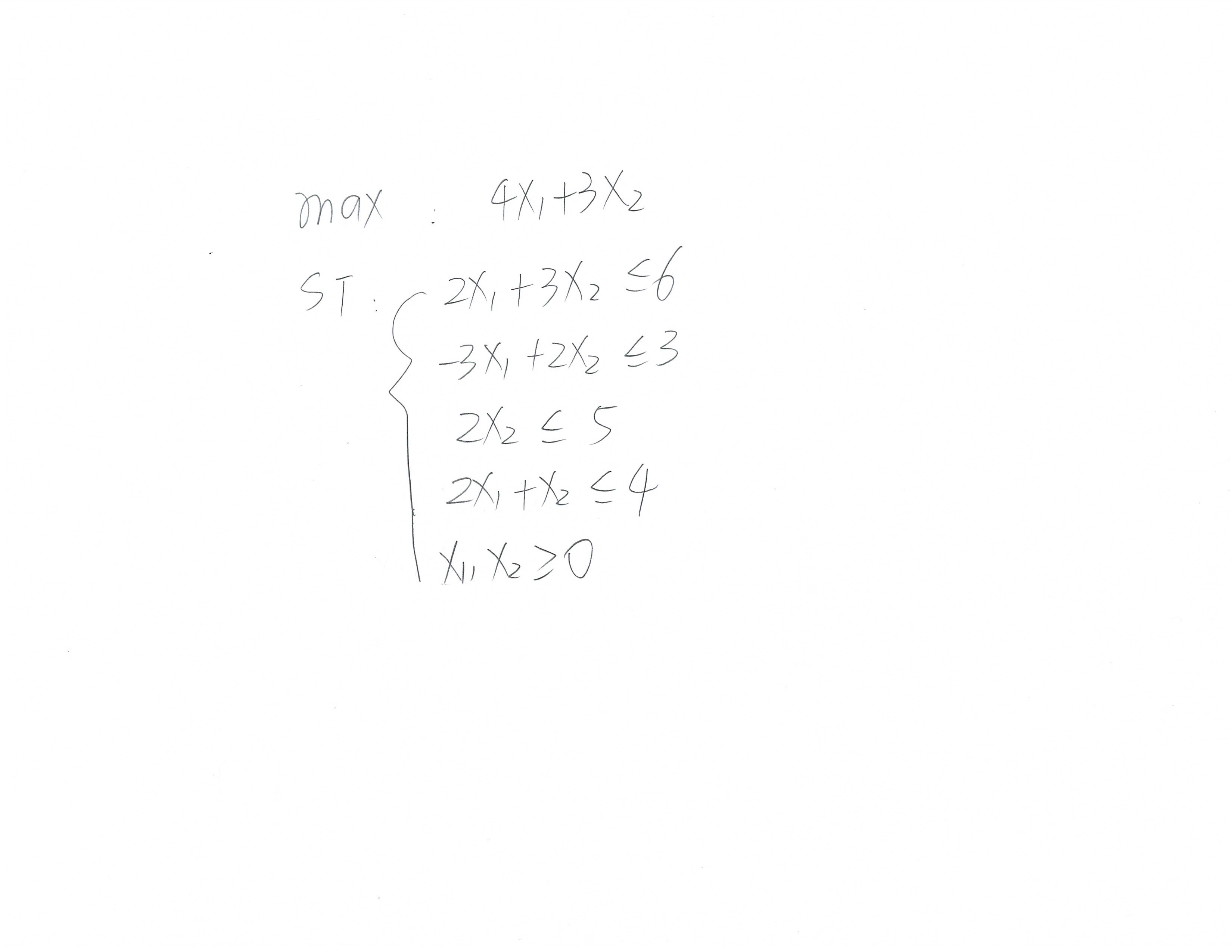
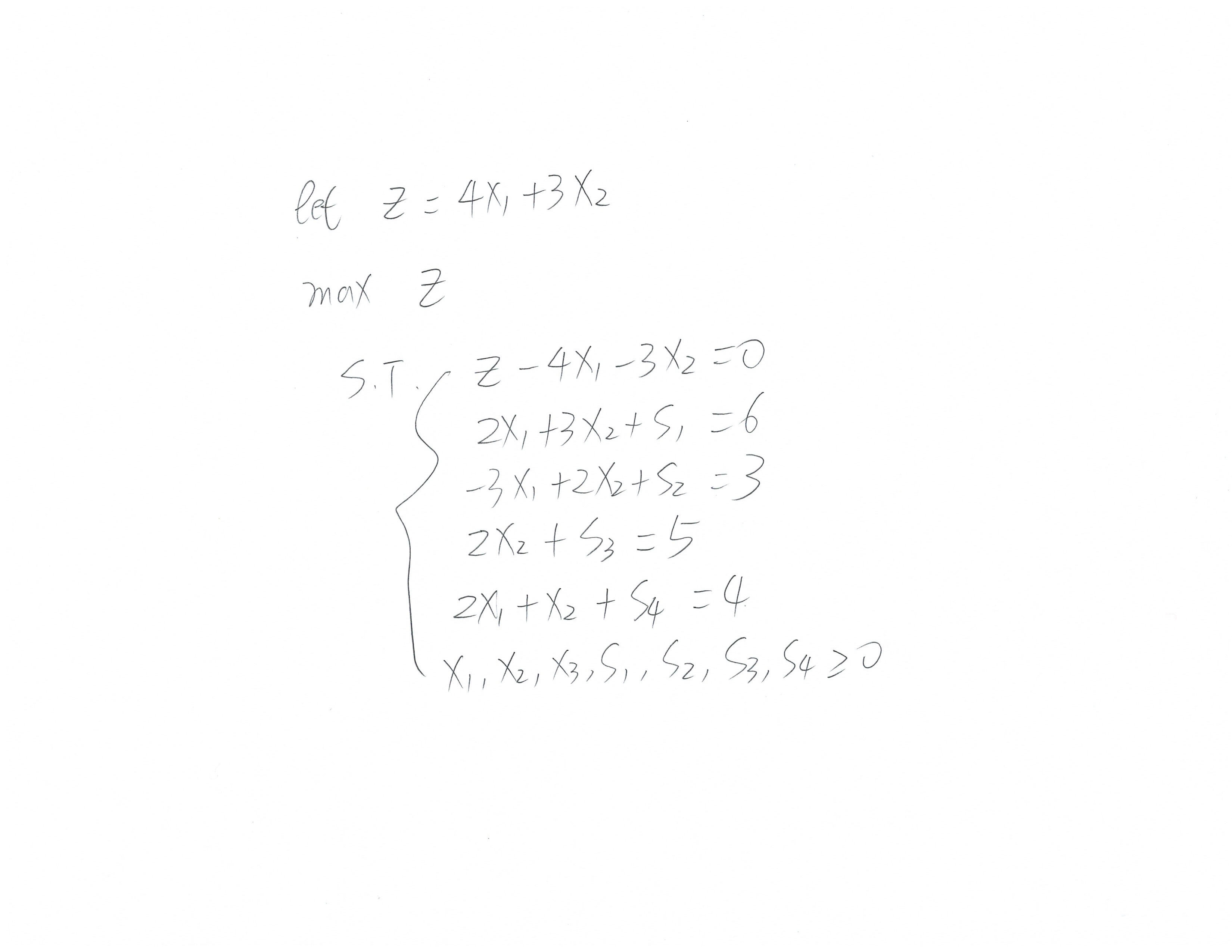
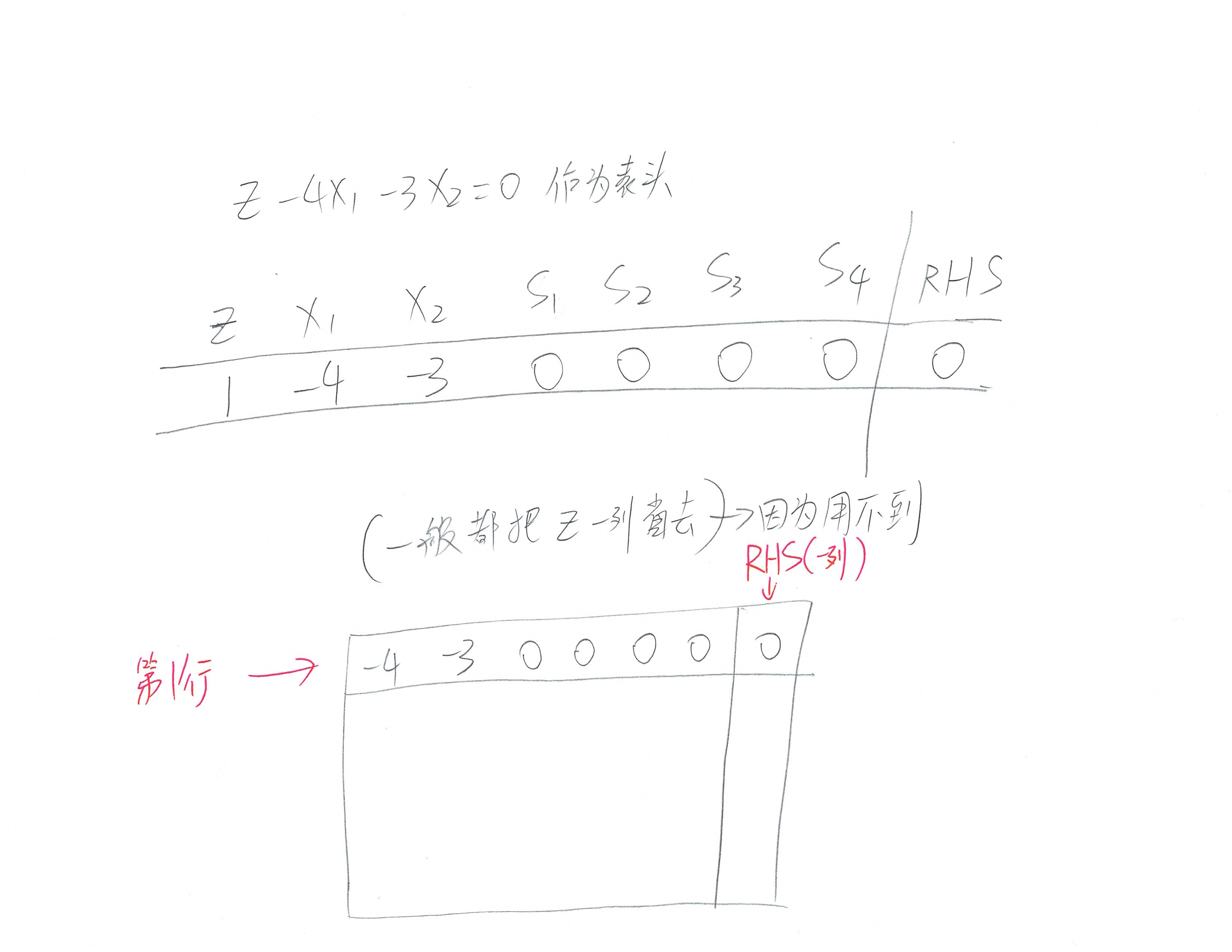
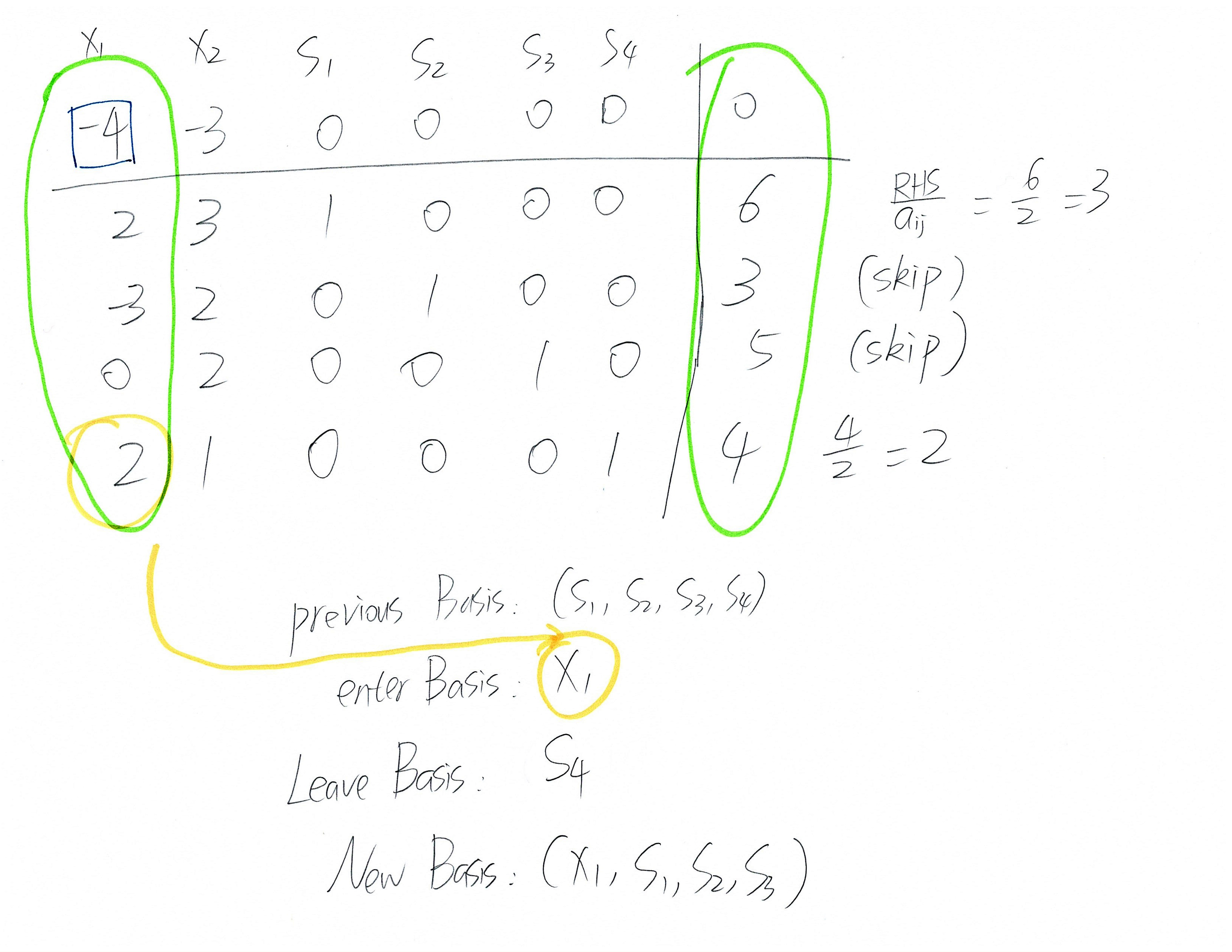
接下来的tableau处理可以参考上面的maximize步骤，每一步都可以用pdf里面的结果进行对照验证
中途的pivot手写的步骤就不重复了，主要是tableau的数值擦来擦去有点麻烦，浪费纸
最后一步：如何从optimal tableau里面读出optimal solution，这一步又忘了，所以还是贴一下：
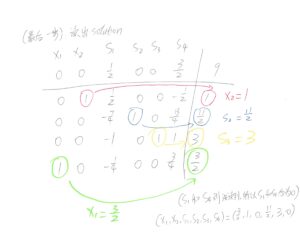
pdf备份：
minimize例题
minimize的例题可以看《最优化理论与算法》p46
用上面的方法制作的tableau如下：
可恶，真的很容易写错，下面的4张图已经勘误过一次了
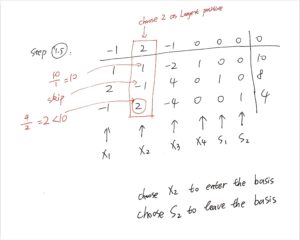
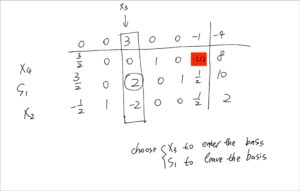
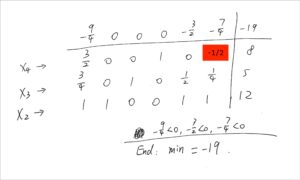
从tableau观察出特殊情况
然后开始学习如何从tableau那里观察出以下特殊情况：
- Degeneracy
- Alternative Optima
🔗 [Tutorial 7: Degeneracy in linear programming] https://ocw.mit.edu/courses/15-053-optimization-methods-in-management-science-spring-2013/1542510abf20fa6145dfb0b1551be6c2_MIT15_053S13_tut07.pdf
整个slide都非常重要，最后有个总结：
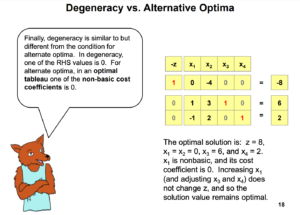
观察Alternative Optima可以用上面这个例子的最后的optimal tableau：
最上面一排的系数从-9/4到-7/4，可以观察到：但凡系数为0，都对应着basis variable；所以这个tableau只有唯一一个optimal solution.
然后再来考虑unbounded
Google搜索“in the simplex method if in pivot column all the entries are negative or zero when choosing leaving variable then”就可以找到很多相同的quiz题，答案都是unbounded.
