Gale–Shapley algorithm - Truxton's blog

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

Table of Contents

介绍，以及手动推算unstable matching pairs

🔗 [Gale–Shapley algorithm - Wikipedia] https://en.wikipedia.org/wiki/Gale–Shapley_algorithm

就是稳定匹配算法/stable matching algorithm.

举例：

假设有100男+100女，各自都有编号。每个女性都维护一个属于自己的优先级表，里面是所有男性成员的优先级排序（从高到低，不能有遗漏，不能重复，正好100个）；每个男性都维护一个属于自己的优先级表，里面是所有女性成员的优先级排序（从高到低，不能有遗漏，不能重复，正好100个）。

所以说这里面一共要存储200个”排序表“，每个排序表100个元素，一共200*100=20000个元素。

Gale-shapley algorithm的作用是：给出一个匹配方案，让这100男+100女的人群中不存在“不稳定风险”/“不稳定匹配”。

上面的“不稳定风险”实际上在正规资料里应该被称为unstable matching，这个笔记里先这么写的原因是方便理解。

🔗 [Stable Matching Solution Visualized] https://uw-cse442-wi20.github.io/FP-cs-algorithm/

最简单的例子：

一点铺垫：

假设有N个男性，N个女性，那么我应该有[mathjax]N![/mathjax]种匹配方案。

最关键的来了：要验证一个现有的匹配是不是stable matching，就要把所有“可能造成unstable matching“的潜在匹配都验证一遍（验证是不是unstable），如果存在一个unstable matching，那整个匹配方案就不稳定，需要换一种匹配方案。

寻找所有的unstable matching = 遍历所有潜在匹配 = 遍历所有当前匹配之外的连接（一共检查[mathjax]N(N-1)[/mathjax]个），而不是检查当前匹配是不是unstable.

比如100男x100女，男性-027当前被匹配到女性-039，要想完全挖掘这个男性-027的潜在不稳定匹配，就要把男性027 x （女性001~女性100，排除女性039）这99个潜在匹配都验证一遍。同理，女性039也要验证99个潜在匹配：女性039 x （男性001~男性100，排除男性027）.

也就是说，对于一个[mathjax]N[/mathjax] x [mathjax]N[/mathjax]的匹配系统，要想验证一个现有的匹配是不是stable matching，就要检验[mathjax]N(N-1)[/mathjax]个潜在匹配。（当然，如果无需列举所有unstable matching，那么只需找到一个unstable matching就可以提前终止寻找）

举例如下：

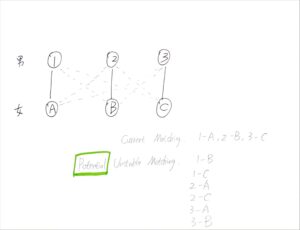
基本顺序就是：

列出所有potential unstable matching（一共[mathjax]N(N-1)[/mathjax]个）（事先决定男-女或者女-男然后跑一遍即可，不需要跑2遍），然后逐一开始检查
对每个要检验的potential unstable matching：看看这个方案是不是比当前方案对男女双方而言都更优。具体大概可以解释为：假设当前的匹配为[mathjax](P, Q)[/mathjax]，[mathjax]Q[/mathjax]在[mathjax]P[/mathjax]心中的排名为第n名。如果现在来了个[mathjax]Q^{\prime}[/mathjax]，她在[mathjax]P[/mathjax]心中的排名比（当前[mathjax]Q[/mathjax]的）第n名靠前，而且[mathjax]P[/mathjax]在[mathjax]Q^{\prime}[/mathjax]心中的排名也比[mathjax]Q^{\prime}[/mathjax]当前匹配的[mathjax]P^{\prime}[/mathjax]靠前，那么[mathjax](P, Q^{\prime})[/mathjax]就是一对unstable matching. 注意到虽然上面提到了[mathjax]P^{\prime}[/mathjax]，也就是[mathjax]Q^{\prime}[/mathjax]当前的匹配对象，但[mathjax]P^{\prime}[/mathjax]只参与排名计算，并不会列入最终的unstable matching结果中。这是因为我们目前只在处理[mathjax](P, Q^{\prime})[/mathjax]的问题，[mathjax]P^{\prime}[/mathjax]还没轮到（或者已经轮完了）。

在🔗 [Stable Matching Solution Visualized] https://uw-cse442-wi20.github.io/FP-cs-algorithm/ 有一个demo，每次都能随机生成一个检查stable matching的题目。

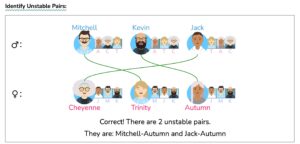
过程如下：

实际上，在做上面这道题的时候可以在某些地方加快一点进度：当我们发现K的当前匹配（对K而言）是最优的时候，所有K相关的potential unstable matching都可以直接打叉了，因为不可能存在比K-A更优的匹配；当然对A而言并不是这样，因为K排在A排名的最后一名，所以我们计算其他unstable matching的时候还要把A带上，最终我们发现J-A和M-A是unstable的。

还有4道题供练习用（不够的话去🔗 [Stable Matching Solution Visualized] https://uw-cse442-wi20.github.io/FP-cs-algorithm/ 随机生成即可）：

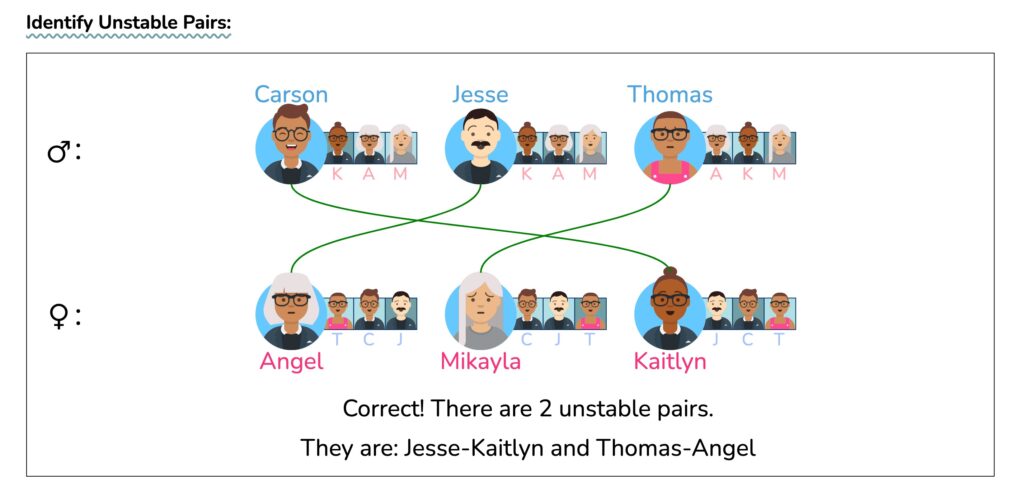
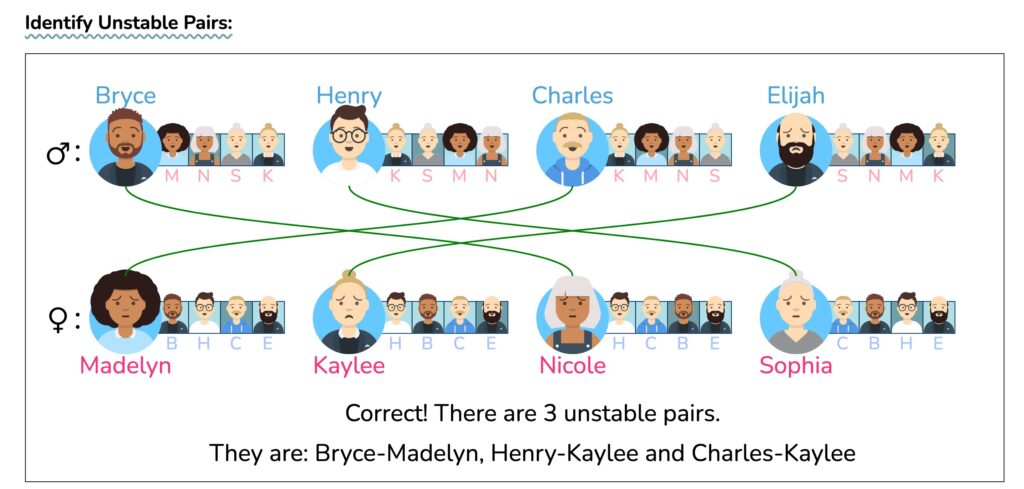
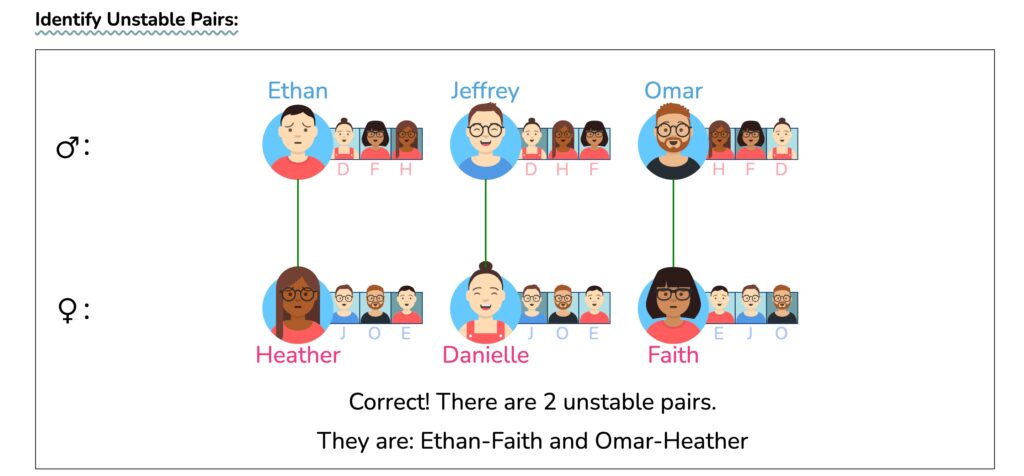
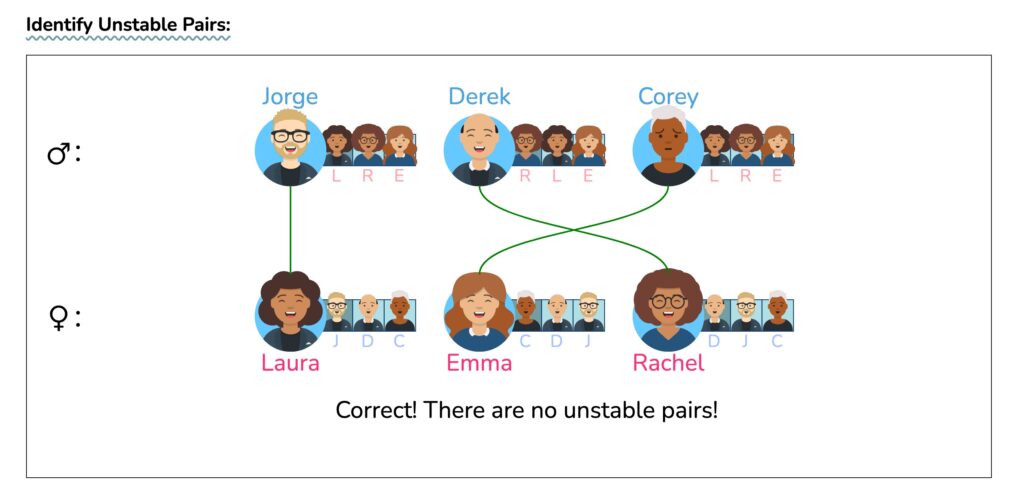
以上就是检验 stable matching的方法。

代码应用

大致思路

为了简便，本笔记会手动实现一个检验 stable matching的算法；stable matching的求解由python matching包提供。

从这里开始：

🔗 [daffidwilde/matching: A package for solving matching games] https://github.com/daffidwilde/matching

搞了半天，发现：

除了stable marriage问题，还有一个student allocation问题，但本篇笔记就暂时不涉及了
matching包只提供对student allocation问题的检验，而且（似乎）只输出true/false，不详细列举
所以stable marriage的检验算法还得自己写一个

大致顺序：

手写一个函数，列举出当前匹配方案的所有unstable matching（如果没有则返回空）
用本笔记上面的例题（来自🔗 [Stable Matching Solution Visualized] https://uw-cse442-wi20.github.io/FP-cs-algorithm/ ）检验函数写得对不对
随机生成100男-100女，偏好完全随机的场景，用matching包去求解stable matching solution
把求解得到的stable matching solution放进第（1）步的函数里验证，如果这个解确实是stable的，那么函数应该返回一个空数组
第（3～4）步的随机场景可以重复多次，看看是不是每次求得的解都是stable的
如果上述程序都按计划执行，那么python [matching]包就是我最终想要的东西，以后可以使用它了。

关于第5步：gale-shapley是一定能得到stable matching solution的，所以只要程序没问题，第5步无论随机多少次都都是stable solution.

https://en.wikipedia.org/wiki/Gale%E2%80%93Shapley_algorithm#Correctness_guarantees

数据输入

首先是python matching包的数据变量写法：

上面这张图的关系以及匹配被写为：

groupA_preferences = {
    "M": ["A", "C", "T"],
    "K": ["A", "T", "C"],
    "J": ["T", "A", "C"],
}

groupB_preferences = {
    "C": ["J", "M", "K"],
    "T": ["M", "J", "K"],
    "A": ["J", "M", "K"],
}

current_matching = {"M": "T", "K": "A", "J": "C"}

用于检验unstable matching的函数

然后是用于检验并列举unstable matching pairs的函数：

def search_dict_key(dict, value):
    for key, val in dict.items():
        if val == value:
            return key


def check_unstable_pairs(groupA_preferences: dict, groupB_preferences: dict, current_matching: dict):
    unstable_pairs = []  # format: [(a1, b1), (a2, b2), ...]
    for groupA_test in groupA_preferences.keys():
        for groupB_test in [val for val in groupB_preferences.keys() if val != current_matching[groupA_test]]:
            if groupA_preferences[groupA_test].index(groupB_test) < groupA_preferences[groupA_test].index(current_matching[groupA_test]) and groupB_preferences[
                groupB_test].index(groupA_test) < groupB_preferences[groupB_test].index(search_dict_key(current_matching, groupB_test)):
                unstable_pairs.append((groupA_test, groupB_test))
    return unstable_pairs

调用：

以及另一个例子：

求解gale-shapley（调包）

简单的例子检验的差不多了，开始进行步骤3~4

先确认python recursion limit至少有1500

import sys

sys.getrecursionlimit()  # 100-100的gale-shapley大概需要1500的recursion limit
# 如果要尝试>100的gale-shapley就需要把recursion limit调大
# sys.setrecursionlimit(4500)

然后开始生成100-100的男女群组，赋予随机偏好优先级列表，用python matching包求解，然后把求解的结果用前面手写的 check_unstable_pairs 检验：

groupA_preferences = {}
groupB_preferences = {}
current_matching = {}

groupA_ids = [f"A_{idx}" for idx in range(0, 100)]
groupB_ids = [f"B_{idx}" for idx in range(0, 100)]
for id_A in groupA_ids:
    groupA_preferences[id_A] = random.sample(groupB_ids, len(groupB_ids))
for id_B in groupB_ids:
    groupB_preferences[id_B] = random.sample(groupA_ids, len(groupA_ids))
groupB_ids_copy = deepcopy(groupB_ids)
for id_A in groupA_ids:
    random_B = random.choice(groupB_ids_copy)
    current_matching[id_A] = random_B
    groupB_ids_copy.remove(random_B)
print(f'Use random matching, there are {len(check_unstable_pairs(groupA_preferences, groupB_preferences, current_matching))} unstable matching pairs')
game = StableMarriage.create_from_dictionaries(
    groupA_preferences, groupB_preferences
)

game_matching = dict(game.solve(optimal="suitor"))
stable_matching = {}
for key, val in game_matching.items():
    stable_matching[str(key)] = str(val)

print(f'Use Gale-shapley algorithm, there are {len(check_unstable_pairs(groupA_preferences, groupB_preferences, stable_matching))} unstable matching pairs')

运行结果（第一行：每次运行的结果都不一样；第二行：要确保为0）

Use random matching, there are 2311 unstable matching pairs
Use Gale-shapley algorithm, there are 0 unstable matching pairs

多次运行以反复验证

最后是第5步：重复上面的“随机100-100多次”：

代码就不贴了，总之就是上面的代码外面套一层while循环，每次都检验一下 check_unstable_pairs 是不是返回了长度为0的数组。

我跑了25000次都是正确的，所以就认为上面的代码没有问题了。

代码汇总

代码汇总：

Last Modified in 2024-10-22