This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.决策树/Decision Tree
Table of Contents
决策树 定义
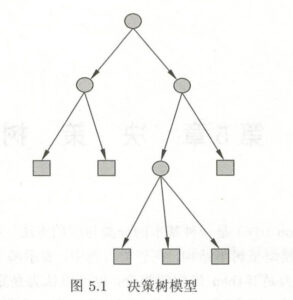
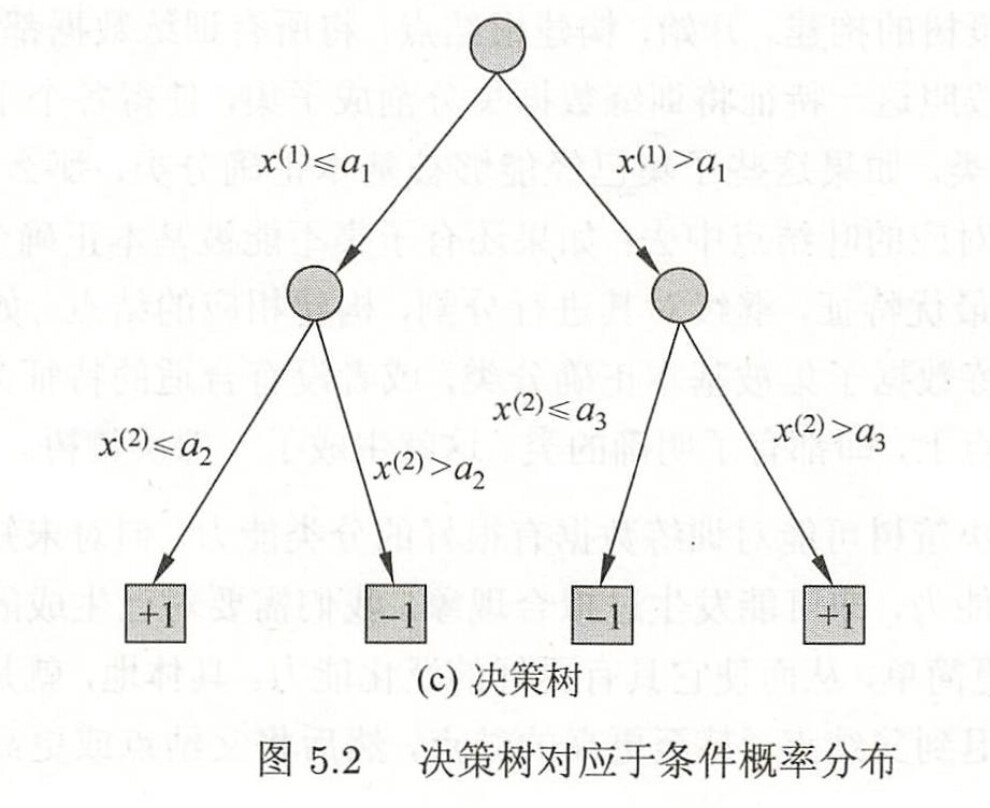
solid example（李航P69）:
决策树的一些问题
决策变量复用
问题1：在上面的p69 example里，原本的decision tree是先用x1决策，然后用x2决策的（这样看起来也最合理），那决策树能否允许先用x2决策再用x1决策呢（最后还要再用x2决策，等于是多了一层）（不讨论是否合理，只讨论是否允许）？
是可以的！这个问题不仅经过gpt/claude的验证，还能在网上找到问答：🔗 [algorithm - Reusing a feature to split regression decision tree's nodes - Stack Overflow] https://stackoverflow.com/questions/67038993/reusing-a-feature-to-split-regression-decision-trees-nodes
在周志华西瓜书上也能找到这个例子：
P88~P90
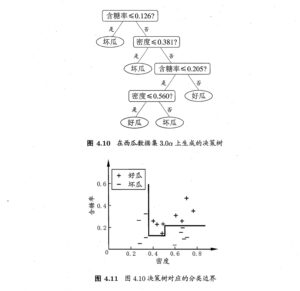
但是注意，在西瓜书里这种决策树出现在“多变量决策树”章节，但它并不是一个多变量决策树！
该问题还有多个延伸和变种，见本笔记后面的讨论（如果确实写了的话）
非-二叉树的决策树
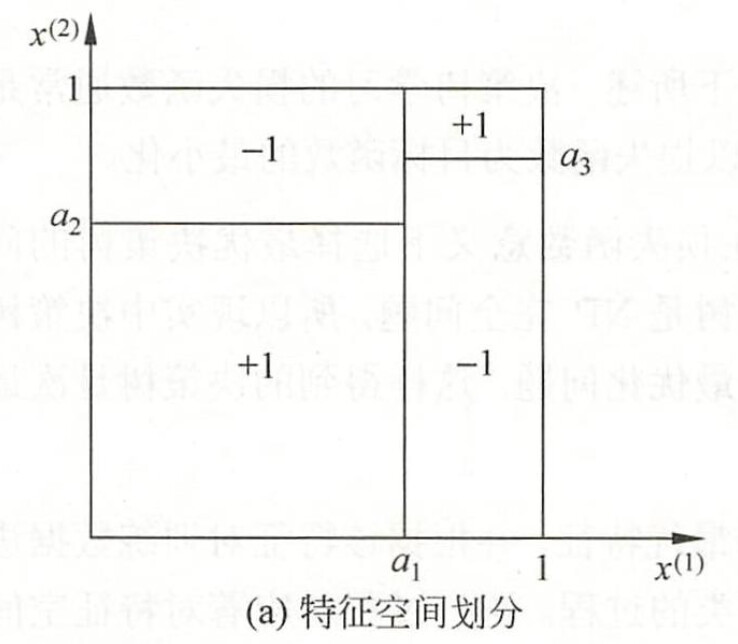
问题2：决策树一定是二叉树吗？
不一定。一个非-二叉树的决策树举例如下：
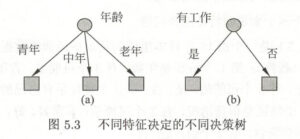
但现实使用代码时又是另一回事。
多变量决策树
问题3：一个内部结点只能对一个变量进行判断吗？
并不是。实际上还有“多变量决策树”：（周志华机器学习P90~P91）
example 1：
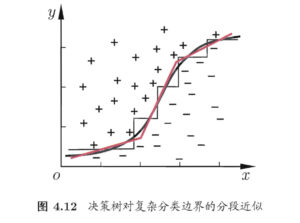
example 2：
但根据gpt的回答，sklearn并不直接提供这样的多决策变量决策树（multivariate decision tree）.
基尼不纯度
gini impurity（基尼不纯度）的计算
🔗 [基尼指数（Gini Impurity）的理解和计算-CSDN博客] https://blog.csdn.net/weixin_41855010/article/details/110312523
计算过程为
左边：[mathjax-d]\frac{105}{105+39}\cdot (1-\frac{105}{105+39})+\frac{39}{105+39}\cdot (1-\frac{39}{105+39})=0.3949652777777778[/mathjax-d]
右边：[mathjax-d]\frac{34}{34+125}\cdot (1-\frac{34}{34+125})+\frac{125}{34+125}\cdot (1-\frac{34}{34+125})=0.3362208773387129[/mathjax-d]
左右两边加权得到的数值，在某些地方被称为“加权基尼不纯度“，有些地方被称为CART cost function（见下面的图）: [mathjax-d](\text{left gini impurity})\cdot \frac{105+39}{105+39+34+125}+(\text{right gini impurity})\cdot \frac{34+125}{105+39+34+125}[/mathjax-d]，最后得到的结果就是0.364，和图中答案一致。
不同决策树算法的决策变量复用
对上面的“变量出现在决策树的多层”问题的进一步讨论。
先贴一个GPT的回复：
问题：
I know that the decision tree algorithm comes in many different versions. My question is: Suppose in a decision tree training, at level x, an internal node is handling k features. In the child nodes of this internal node, do they handle k features or k-1 features? Is there an algorithm that handles all features at all levels?
回复：
In a decision tree algorithm, the number of features handled at each node depends on the specific tree-building method:
- Standard Decision Trees (CART, ID3, C4.5, etc.)
- At each internal node, the algorithm selects the best feature (among the k available features) to split the data.
If the selected feature is not reusable in child nodes (e.g., ID3, C4.5 for categorical features), then child nodes will handle k−1 features.我对这个结论有疑问，所以下面会单独拉出来讨论- If the feature can be reused in child nodes (e.g., CART for numerical features where threshold splits allow reuse), then child nodes still handle k features.
- Algorithms that Consider All Features at Every Level
- Random Forests: Each tree in the ensemble randomly selects a subset of k′ features at each node, but within a tree, the number of features available at child nodes depends on whether features can be reused.
- Oblique Decision Trees: These use linear combinations of all k features at each node, meaning all features can contribute to splits at every level.
- Some Modern Variants (e.g., Totally Randomized Trees, Neural Decision Trees): These might handle all k features at every node, depending on their construction method.
So, if you are looking for an algorithm where all features are considered at every level, Oblique Decision Trees or some specialized variants of Neural Decision Trees might be suitable. Standard decision trees typically reduce features (if categorical and non-reusable) or allow reuse (for numerical features).
下面再来讨论上面回答中略有疑惑的地方：当一个internal node处理一个“3-category feature”的时候，它会分出2叉还是3叉？如果分出2叉，后续是否会对分离出来的categories进行进一步分割？
gpt的回复：
决策边界（带练习题）
在经历上面的gpt学习以后至少可以看出，对连续变量而言，“变量复用”是非常非常常见的决策树训练结果。google images关键词：decision tree decision boundary，就能找出很多很多例子
练习题：
已知下面的决策树结果，画出它的决策树状图（数值具体多少标在图中了）
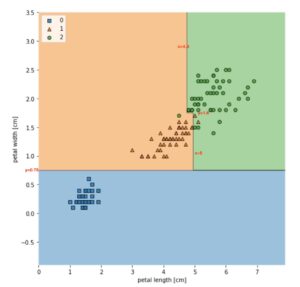
其中一个答案（答案不唯一，很容易自己验证）：
