This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.2024-02-28，想要复健更多音频信号的知识，眼睛瞄向了Autoregression model (AR)，这玩意我之前就一直没学会到底是什么原理。
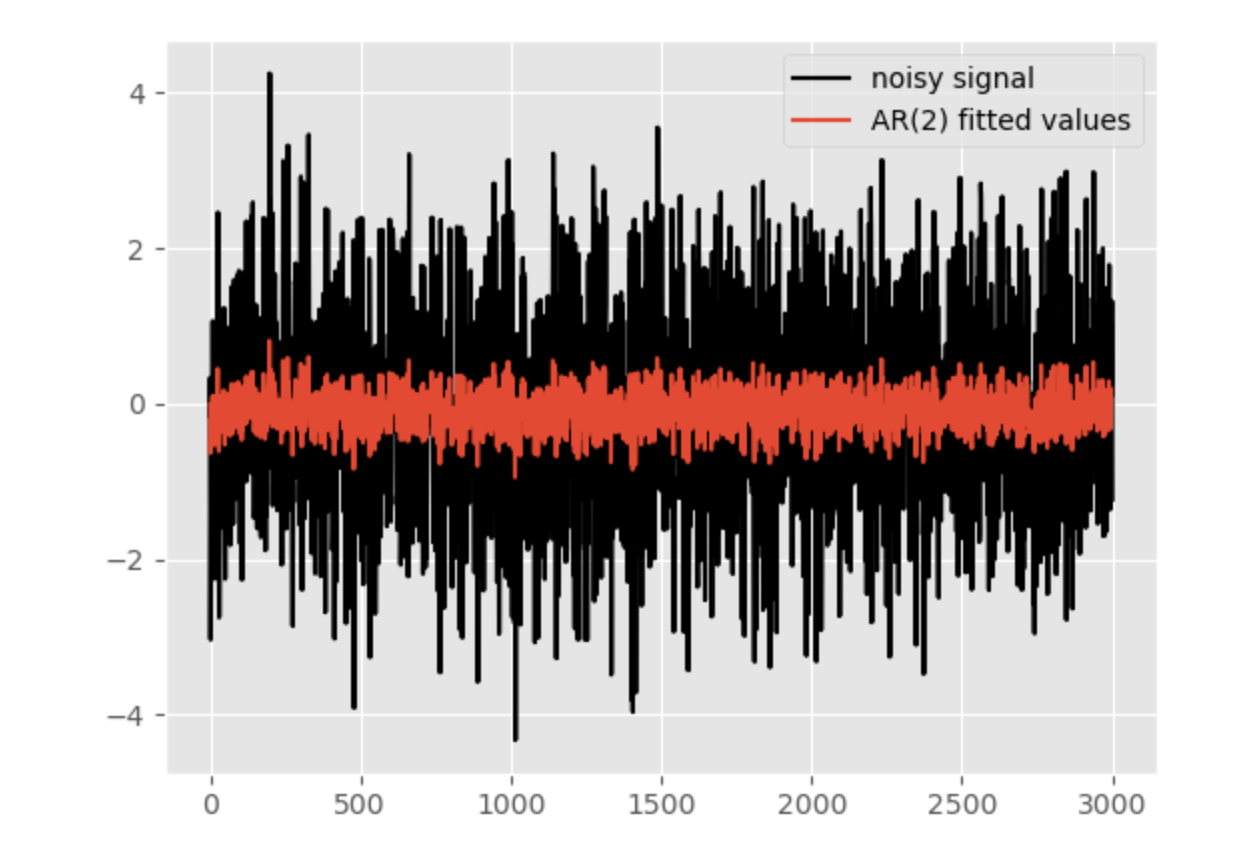
很遗憾，这次也没学会AR的推导，只是写了点简单的代码当作AR的应用（降噪）。
主要参考🔗 [python - Can I use AutoRegression modelling for signal denoising? - Stack Overflow] https://stackoverflow.com/questions/66799308/can-i-use-autoregression-modelling-for-signal-denoising
AR降噪的整个过程大概是这样：
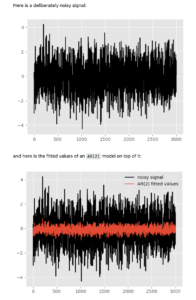
上面的链接的回答里贴出了一个非常容易上手实践的方法（直接调包，不需要自己手写代码）：
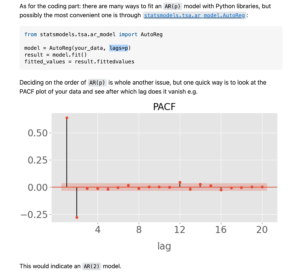
AR(p)的参数p（可以取1, 2, 3, 4....) 需要自己去尝试，所以下面的代码打算这么做：
先生成一段这样的音频信号：
[mathjax-d]x(t)=\sin(2\pi\cdot 440\cdot t)+\epsilon, \epsilon \sim \mathcal{N}(\mu=0,\,\sigma^{2}=1)[/mathjax-d]
注意到440Hz sinewave的振幅A=1，而噪声高斯分布的方差达到了1（噪声分布长这样），这应该是一个非常噪音的音频了，用常规sonic visualizer频谱图也根本看不出任何东西。
注意耳朵
首先写了一个非常暴力的python代码去硬试1~20范围内最佳的AR(p)参数p（本文参考的stackoverflow链接里使用PACF评估效果，但我没找到这个参数在哪里，所以就用p值了：p值越高 = model fit效果越好）
非常吃资源
import numpy as np
from scipy.io import wavfile
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg
bits = 16
sr = 44100
def save_wav(y, filename):
# Scale the signal to fit the desired bit depth range
y_scaled = np.int16(y * (2 ** (bits - 1) - 1))
# Save the wav file
wavfile.write(filename, sr, y_scaled)
if __name__ == "__main__":
t = np.linspace(0, 10, 10 * sr)
y_sinewave = np.sin(2 * np.pi * (440 * t))
y_noise = np.random.normal(0, 1, size=10 * sr)
y = y_sinewave + y_noise
save_wav(y, "noised_sinewave.wav")
p_value_lst = []
for lags in range(1, 20):
p_value = 0
for i in range(0, 50):
model = AutoReg(y, lags=lags)
result = model.fit()
fitted_values = result.fittedvalues
# print(result.summary())
# print(result.pvalues[0])
p_value += result.pvalues[0]
# save_wav(fitted_values, "output.wav")
print("lag %d, avg p-value: %f" % (lags, p_value / 50))
p_value_lst.append(p_value / 50)
输出结果：
lag 1, avg p-value: 0.745827
lag 2, avg p-value: 0.800104
lag 3, avg p-value: 0.836113
lag 4, avg p-value: 0.859618
lag 5, avg p-value: 0.877370
lag 6, avg p-value: 0.891994
lag 7, avg p-value: 0.902592
lag 8, avg p-value: 0.911035
lag 9, avg p-value: 0.916034
lag 10, avg p-value: 0.918109
lag 11, avg p-value: 0.921571
lag 12, avg p-value: 0.922424
lag 13, avg p-value: 0.921423
lag 14, avg p-value: 0.923185
lag 15, avg p-value: 0.921387
lag 16, avg p-value: 0.919400
lag 17, avg p-value: 0.914848
lag 18, avg p-value: 0.912148
lag 19, avg p-value: 0.908427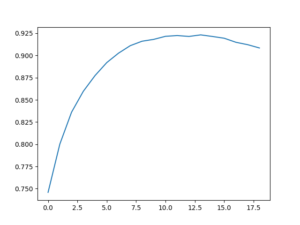
最后发现p=10~14的效果最好，所以接下来的代码里就用p=13了
经过一轮AR(p=13)的处理，输出音频如下：
注意耳朵
其实这个时候降噪效果已经非常可观了
有一轮AR自然就免不了多轮AR，把代码稍微改一改变成一个迭代，每次AR(13)的降噪产物丢到下一个AR(13)里去循环
import matplotlib.pyplot as plt
import numpy as np
from scipy.io import wavfile
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg
bits = 16
sr = 44100
def save_wav(y, filename):
# Scale the signal to fit the desired bit depth range
y_scaled = np.int16(y * (2 ** (bits - 1) - 1))
# Save the wav file
wavfile.write(filename, sr, y_scaled)
if __name__ == "__main__":
t = np.linspace(0, 10, 10 * sr)
y_sinewave = np.sin(2 * np.pi * (440 * t))
y_noise = np.random.normal(0, 1, size=10 * sr)
y = y_sinewave + y_noise
save_wav(y, "wav_output/noised_sinewave.wav")
model = AutoReg(y, lags=13)
result = model.fit()
fitted_values = result.fittedvalues
# print(result.summary())
print(result.pvalues[0])
save_wav(fitted_values, "wav_output/output_init.wav")
iteration_p_value = []
for i in range(0, 80):
model = AutoReg(fitted_values, lags=13)
result = model.fit()
fitted_values = result.fittedvalues
# print(result.summary())
print("%d: %f" % (i, result.pvalues[0]))
iteration_p_value.append(result.pvalues[0])
save_wav(fitted_values, "wav_output/output_round%d.wav" % i)
plt.figure()
plt.plot(iteration_p_value)
plt.xlabel("iteration")
plt.ylabel("p value")
plt.savefig("iteration_80.png")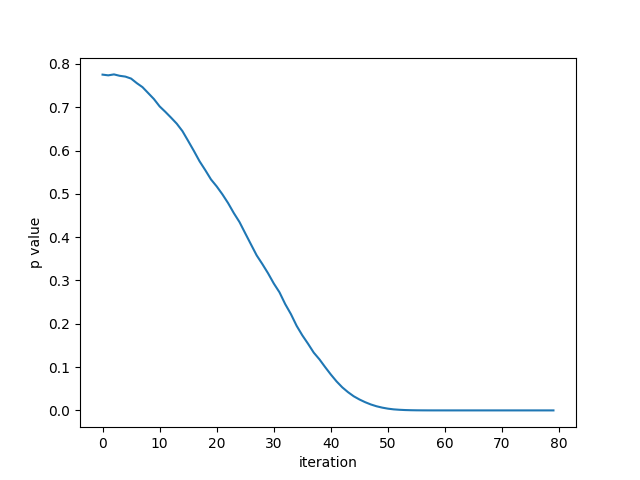
注意：每次跑上面这个程序的收敛结果都不太一样，因为每次随机的信号不同，做第一次AR(13)时的p value也不同，有的时候从0.95开始下降，有的时候从0.8开始下降。但一般都能在80个iteration里跑到p value = 0
规律：随着不断迭代，降噪后的音频声音越来越小，噪声也越来越柔和，但最终还是没有得到一个特别纯净的440Hz sinewave，这种迭代思路具体有没有用（算不算进一步降噪）有待商榷。
重新把整个过程的音频文件贴出来：
最开始的：注意耳朵
第1轮AR(13)：注意耳朵
第26轮AR(13)：
第55轮AR(13)：
第80轮AR(13)：
第80轮AR(13)对应的频谱图：
